最长公共子序列-动态规划DP

因为比较有用，所以就转来了，原文地址http://www.nocow.cn/index.php/%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97

概述

最长公共子序列：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。 令给定的字符序列X="x0，x1，...，xm -1"，序列Y="y0，y1，...，yk-1"是X的子序列， 存在X的一个严格递增下标序列，使得对所有的j=0，1，...，k-1，有xij= yj。例如，X="ABCBDAB"，Y="BCDB"是X的一个子序列。 给定两个序列A和B，称序列Z是A和B的公共子序列，是指Z同是A和B的子序列。 问题要求已知两序列A和B的最长公共子序列。

分析

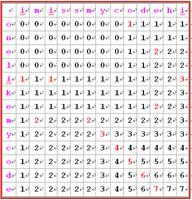
本题初看有些类似线形动态规划，但经过仔细审题发现用矩阵类动态规划更好理解， 如下图所显示，我们把两个字符串看作矩阵的横纵轴： 首先读入数据时，把两个字符相同的标记成1，不相同的地方标记成0；

很容易证明，如果能形成公共子序列，则最长子序列一定是从某个位置开始的对角线的长度，所以我们需要做的就是统计对角线的长度，DP方程就为if a[i,j]=1 then d[i,j]:=d[i-1,j-1]+1;

经过循环我们就可以把上表转化成:

因此我们只需记录在循环中的最大值就是我们要的最长公共子序列的长度；

代码：

      d[0,0]:=0;
      for i:=1 to n do d[i,0]:=0;
      for j:=1 to m do d[0,j]:=0; //初始化
      for i:=1 to n do
        for j:=1 to m do
           if s1[i]=s2[j] then //等价于 if a[i,j]=1 then
             d[i,j]:=d[i-1,j-1]+1
           else
           begin
               if d[i-1,j]>d[i,j-1] then
                  d[i,j]:=d[i-1,j]
               else d[i,j]:=d[i,j-1];
           end;

 

优化：但是在0和1的矩阵中找最长的1对角线序列又要花去一定的时间。通过改进矩阵的生成方式和设置标记变量，可以省去这部分时间。

当字符匹配的时候，我们并不是简单的给相应元素赋上1，而是赋上其左上角元素的值加一。

我们用两个标记变量来标记矩阵中值最大的元素的位置，在矩阵生成的过程中来判断当前生成的元素的值是不是最大的，据此来改变标记变量的值，那么到矩阵完成的时候，

最长匹配子串的位置和长度就已经出来了.这样做速度比较快，但是花的空间太多。我们注意到在改进的矩阵生成方式当中，每生成当前一层，前面的那一层就已经没有用了。

因此我们只需使用一维数组即可。可以自己写一下。

变种之一：字串距离

 

顺便附上HDOJ Common Subsequence AC代码一份

#include <cstdio> #include <cstring> int a[1000][1000]; int main(){ char x[1000], y[1000]; int n, m, i, j, ans; while(~scanf("%s%s",x,y)){ n = strlen(x); m = strlen(y); ans = -1; memset(a,0,sizeof(a)); for(i = 0; i < n; i++){ for(j = 0; j < m; j++){ if(x[i] == y[j]) a[i+1][j+1] = 1; else a[i+1][j+1] = 0; if(a[i+1][j+1] > ans) ans = a[i+1][j+1]; } } for(i = 1; i <= n; i++){ for(j = 1; j <= m; j++){ if(a[i][j]) a[i][j] = a[i-1][j-1] + 1; else{ a[i][j] = (a[i-1][j]>a[i][j-1])?a[i-1][j]:a[i][j-1]; } if(a[i][j] > ans) ans = a[i][j]; } } /* for(i = 1; i <= n; i++){ for(j = 1; j <= m; j++){ if(j) putchar(' '); printf("%d",a[i][j]); } putchar(10); } */ printf("%d/n",ans); } return 0; }