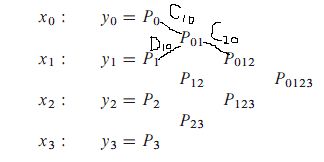Neville 算法解多项式插值
原文链接:http://blog.csdn.net/zhangxaochen/article/details/8100012
原理图如下:
Numerical Recipes 随书附带的代码:(xa, ya 是n个样本点的坐标值数组, x 是待求点的横坐标, 输出值为 y, dy, 其中dy 表示误差)
void NR::polint(Vec_I_DP &xa, Vec_I_DP &ya, const DP x, DP &y, DP &dy)
{
int i,m,ns=0;
DP den,dif,dift,ho,hp,w;
int n=xa.size();
Vec_DP c(n),d(n);
dif=fabs(x-xa[0]);
for (i=0;i<n;i++) {
if ((dift=fabs(x-xa[i])) < dif) {
ns=i;
dif=dift;
}
c[i]=ya[i];
d[i]=ya[i];
}
y=ya[ns--];
for (m=1;m<n;m++) {
for (i=0;i<n-m;i++) {
ho=xa[i]-x;
hp=xa[i+m]-x;
w=c[i+1]-d[i];
if ((den=ho-hp) == 0.0) nrerror("Error in routine polint");
den=w/den;
d[i]=hp*den;
c[i]=ho*den;
}
y += (dy=(2*(ns+1) < (n-m) ? c[ns+1] : d[ns--]));
}
}
其中有两个数组 c[n], d[n], 分别表示后一列相对前一列的增量(因为有两个分支),如上面第一张图所示,事实上我一直不明白弄这个增量有什么深意,好像没有降低时间复杂度, 反而增加了编程的复杂度。 如果有前辈恰好了解这个深意, 盼赐教哇。
个人实现的代码就比较简单:
void MyPolint(const double* xa, const double* ya, const int n, const double x, double& y){
double* p=new double[n];
for(int i=0; i<n; i++){
p[i]=ya[i];
}
for(int k=1; k<n; k++){
for(int i=0; i<n-k; i++){
double factor1=x-xa[i+k],
factor2=xa[i]-x;
p[i]=(factor1*p[i]+factor2*p[i+1])/(factor2+factor1);
}
}
y=p[0];
}
测试代码:
#include "nr.h"
using namespace std;
using namespace NR;
void MyPolint(const double* xa, const double* ya, const int n, const double x, double& y);
void main(){
const int n=4;
DP xarr[n]={-1, 0, 1, 2};
//DP yarr[n]={-2, 0, 2, 10};//曲线为: y=x^3+x
DP yarr[n]={1, 0, -1, 4}; //曲线为: y=x^3-2x
Vec_I_DP xa(xarr, n);
Vec_I_DP ya(yarr, n);
DP x=1.5;
DP y=INT_MAX,
dy=INT_MAX;
polint(xa, ya, x, y, dy);
printf("y, dy: %lf, %lf\n", y, dy); // 4.875, 1.875, √
//-------------我的函数
MyPolint(xarr, yarr, n, x, y);
printf("y: %lf\n", y);
}
输出结果:
y, dy: 0.375000, 1.875000
y: 0.375000
因为个人也没大理解那个 dy凭什么就是误差,所以自己实现的函数里就没算这个 dy
原文链接:http://blog.csdn.net/zhangxaochen/article/details/8100012
{{OVER}}