- Serverless架构下的持续交付实践
软件工程实践
软件工程最佳实践AI软件构建大数据系统架构serverless架构运维ai
Serverless架构下的持续交付实践关键词:Serverless架构、持续交付、DevOps、无服务器计算、自动化部署摘要:本文深入探讨了Serverless架构下的持续交付实践。首先介绍了Serverless架构和持续交付的背景知识,接着解释了相关核心概念及其关系,详细阐述了核心算法原理与操作步骤,通过数学模型加深理解,结合实际项目案例展示了代码实现与解读,探讨了实际应用场景,推荐了相关工具
- 重排利器:行列式点过程(DPP)在推荐系统中的应用
Jay Kay
推荐算法数学建模推荐算法
在推荐系统的重排阶段,我们常面临结果同质化问题——精排结果相似物料扎堆,导致用户体验单调。行列式点过程(DeterminantalPointProcesses,DPP)通过数学建模相关性与多样性的平衡,成为解决该问题的经典方案。一、DPP的核心思想DPP将推荐列表视为一个点过程,其核心是计算子集出现的概率。给定候选集(Z)(精排输出的Top-N物料),DPP定义子集(Y\subseteqZ)出现的
- Cesium快速入门到精通系列教程十:实现任意多个蜂巢似六边形组合
duansamve
cesiumcesium
要实现完美的正六边形蜂巢排列,关键在于精确计算每个六边形的顶点位置和排列方式。以下是Cesium1.106中优化后的完整实现方案:正六边形几何原理正六边形的特性:所有边长相等(设为radius)中心到每个顶点的距离相等(外接圆半径)相邻六边形中心间距为√3*radius行间距为1.5*radiusCesium.Ion.defaultAccessToken='你的defaultAccessToken
- 非关系型数据库在数据库领域的崛起与应用
数据库管理艺术
数据库专家之路大数据AI人工智能MCP&AgentSQL实战数据库nosql网络ai
非关系型数据库在数据库领域的崛起与应用关键词:非关系型数据库、关系型数据库、崛起原因、应用场景、数据库领域摘要:本文主要探讨了非关系型数据库在数据库领域的崛起与应用。首先介绍了非关系型数据库的背景,包括目的、预期读者等内容。接着详细解释了非关系型数据库、关系型数据库等核心概念,并阐述了它们之间的关系。然后深入讲解了非关系型数据库的核心算法原理、数学模型和公式。通过项目实战展示了非关系型数据库的实际
- AI优化算法实战:使用粒子群优化求解复杂工程问题
AI学长带你学AI
ai
AI优化算法实战:使用粒子群优化求解复杂工程问题关键词:粒子群优化(PSO)、全局优化、工程问题、智能算法、参数调优摘要:本文以“鸟群觅食”为灵感来源,深入浅出地讲解粒子群优化(ParticleSwarmOptimization,PSO)算法的核心原理,并通过机械结构轻量化设计的实战案例,展示其在复杂工程问题中的应用。文章从算法起源到数学模型,从代码实现到工程落地,层层拆解技术细节,帮助读者快速掌
- Cesium快速入门到精通系列教程十一:Cesium1.74中高性能渲染上万Polyline
duansamve
cesiumcesium
在Cesium1.74中,高性能渲染大量线条的核心在于PrimitiveAPI的批量处理、着色器优化和数据合并策略。以下是结合多个技术方案的最佳实践和完整代码实现:一、高性能渲染方案选择PrimitiveAPI批量渲染优势:直接操作几何体实例,减少Entity的开销,支持合并几何数据降低DrawCall。关键类:PolylineGeometry+GeometryInstance+Primitive
- 深度剖析AI人工智能在自动驾驶中的系统优化
AI云原生与云计算技术学院
人工智能自动驾驶机器学习ai
深度剖析AI人工智能在自动驾驶中的系统优化关键词:AI人工智能、自动驾驶、系统优化、传感器融合、决策算法摘要:本文深入探讨了AI人工智能在自动驾驶系统中的优化问题。从自动驾驶的背景入手,详细解释了相关核心概念,如传感器、决策算法等。阐述了这些核心概念之间的关系,介绍了核心算法原理和具体操作步骤,还通过数学模型和公式进行了理论支持。给出了项目实战案例,分析了实际应用场景,推荐了相关工具和资源,最后探
- 量化价值投资入门:Fama-French三因子模型详解与实战应用
量化价值投资入门到精通
ai
量化价值投资入门:Fama-French三因子模型详解与实战应用关键词:量化投资、Fama-French三因子模型、价值投资、因子投资、资产定价、Python实现、投资组合管理摘要:本文深入解析Fama-French三因子模型的理论基础、数学原理和实际应用。作为现代金融学最重要的资产定价模型之一,三因子模型通过市场因子、规模因子和价值因子解释股票收益差异。我们将从模型起源开始,详细讲解其数学表达和
- 暑假复习篇之运算与逻辑
清梚不喝粥
25暑假java算法后端
运算符算术运算符:+-*/%(取余)【优先级与数学上的优先级一致】赋值运算符:=、+=、-=、*=、/=、%=、++、--比较运算符:==、!=、>、=、>(向右位移)>>>(无符号向右位移)<<(向左位移)位运算符:&(按位与)、|(按位或)、^(按位异或)运算符:①一个浮点与整数运算时的结果还是浮点数②一个整数除另一个整数的结果还是整数整除③注意不同数据类型的常规类型【注意范围问题】赋值运算符
- 从 “啃书焦虑” 到 “项目通关”:NLP 学习的破局之道
木旭林晖
自然语言处理学习人工智能
嘿,你好。在CSDN上潜水这么久,我总能看到很多像你我当年一样,怀揣着NLP大厂梦的同学。我猜,你的收藏夹里一定塞满了“NLP必读清单”,书架上可能还放着那本厚得像砖头一样的《统计学习方法》或者“龙书”。每天深夜,你可能都在跟一个又一个复杂的数学公式死磕。什么最大熵模型、什么CRF(条件随机场)的推导……你觉得自己离“精通”越来越近,但心里却越来越慌。为什么慌?因为你打开招聘软件,看到JD(职位描
- go build -gcflags 参数学习
岳来
golanggolang学习开发语言
文章目录一、常用编译选项二、使用模式与包匹配规则三、应用场景与注意事项四、其他相关参数五、删除-gcflagsall=-N-l对构建的影响参考文档gobuild的-gcflags参数用于向Go编译器(gotoolcompile)传递额外选项,控制编译行为。其格式为-gcflags="[pattern=]arglist",其中pattern定义作用范围,arglist是空格分隔的编译选项。以下是关键
- Three.js学习10:几何体(1)-平面几何体
stones4zd
three.js学习
-----------------------------华丽的分割线---------------------相关代码均已上传到gitee中:myThree:学习Three.js,努力加油~!Gitee静态演示地址:ThreeJS演示页面-----------------------------华丽的分割线---------------------一、几何体GeometryThree.js中物体
- 什么是 PoW(工作量证明,Proof of Work)
MonkeyKing.sun
区块链
共识算法(ConsensusAlgorithm)是区块链的“心脏”,它决定了多个节点在没有中央机构的前提下,如何就“谁来记账”达成一致。什么是PoW(工作量证明,ProofofWork)定义:工作量证明(ProofofWork,简称PoW)是一种共识机制,要求节点通过解决一个高难度数学问题,来获得记账权。第一个算出答案的节点获得“打包交易→生成区块→获取奖励”的权利。它是比特币、以太坊(1.0)等
- Three.js开发必备:几何体BufferGeometry顶点详解
天生我材必有用_吴用
three.jsthreeJS
目录几何体顶点位置数据和点模型对象Points缓冲类型几何体BufferGeometry顶点模型第一步、创建一个空的几何体对象第二步、添加顶点数据第三步、3个为一组,表示一个顶点的xyz坐标第四步、设置几何体顶点属性与点材质第五步、导出点模型第六步、场景中引入添加点模型第七步、查看效果线模型Line渲染顶点数据第一步、设置线材质对象第二步、创建线模型对象第三步、场景中引入添加线模型第四步、查看效果
- 实现make_power_of_two函数
洞阳
c++面试c++
目录代码make_power_of_two函数解析:将数值转换为大于等于它的最小2的幂一、函数功能与核心逻辑二、代码实现与逐行解析三、逐步骤原理解析四、位运算的数学原理五、不同输入的转换示例六、算法复杂度与适用场景七、与其他实现方式的对比八、注意事项总结代码该函数将任意n转换为大于等于n的最小2的幂(如n=10→16,n=16→16)size_tmake_power_of_two(size_tn)
- 人工智能大模型原理与应用实战:大模型在金融风控中的应用
AI天才研究院
LLM大模型落地实战指南大数据人工智能语言模型AILLMJavaPython架构设计AgentRPA
文章目录人工智能大模型原理与应用实战:大模型在金融风控中的应用01.背景介绍1.1金融风控的挑战1.2大模型的优势2.核心概念与联系2.1大模型在金融风控中的应用场景2.2大模型与传统风控技术的结合3.核心算法原理具体操作步骤3.1基于大模型的欺诈检测3.2基于大模型的信用评估4.数学模型和公式详细讲解举例说明4.1逻辑回归模型4.2XGBoost模型5.项目实践:代码实例和详细解释说明5.1基于
- 浅谈卷积神经网络(CNN)
cyc&阿灿
cnn人工智能神经网络
卷积神经网络(ConvolutionalNeuralNetworks,CNN)作为深度学习领域最具影响力的架构之一,已在计算机视觉、自然语言处理、医学影像分析等领域取得了革命性突破。本文将系统全面地剖析CNN的核心原理、关键组件、经典模型、数学基础、训练技巧以及最新进展,通过理论解析与代码实践相结合的方式,帮助读者深入掌握这一重要技术。一、CNN基础与核心思想1.1传统神经网络的局限性在处理图像等
- JavaScript 核心对象深度解析:Math、Date 与 String
小宁爱Python
前端javascript开发语言ecmascript
JavaScript作为Web开发的核心语言,提供了丰富的内置对象来简化编程工作。本文将深入探讨三个重要的内置对象:Math、Date和String,通过详细的代码示例和综合案例帮助你全面掌握它们的用法。一、Math对象Math对象提供了一系列静态属性和方法,用于执行各种数学运算,无需实例化即可使用。常用属性:console.log(Math.PI);//圆周率:3.141592653589793
- 从入门到精通:前端工程师必学的 JSON 全解析
前端视界
前端json状态模式ai
从入门到精通:前端工程师必学的JSON全解析关键词:JSON、前端工程师、数据交换、JavaScript、数据格式摘要:本文围绕前端工程师必学的JSON展开全面解析。从JSON的基本概念、背景知识入手,深入探讨其核心原理、算法实现、数学模型等方面。通过详细的代码示例和实际应用场景分析,帮助前端工程师从入门到精通掌握JSON的使用。同时,提供了丰富的学习资源、开发工具和相关论文推荐,最后对JSON的
- landsat卫星遥感影像下载、处理教程
一条破秋裤
个人笔记笔记
1.landsat数据下载USGS网址:EarthExplorer参考链接:USGS下载遥感影像——以Landsat影像下载为例_usgs怎么下载遥感影像-CSDN博客L1TP数据进行了几何校正和辐射校正,L2SP数据在此基础上,进一步处理后的数据,通常包括地表反射率和其他相关的地表特征信息。但是L1和L2的选择需要根据实际需求。这里我们选择下载landsat8-9L1数据目前是可以直接在浏览器下
- 【网络安全】网络安全中的离散数学
flyair_China
安全架构
一、离散数学核心知识点与网络安全映射1.数论(NumberTheory)知识点安全应用场景实例说明质因数分解RSA公钥加密大整数分解难题(2048位密钥需数万年破解)模运算Diffie-Hellman密钥交换利用(gamodp)实现安全协商欧拉定理RSA加密/解密me*d≡m(modn)保障解密还原中国剩余定理高效解密优化RSA-CRT加速解密运算达70%2.代数结构(AlgebraicStruc
- 机器学习中的数学:数学建模常用知识点-1
数字化与智能化
机器学习中的数学机器学习凸函数泰勒公式Jensen不等式
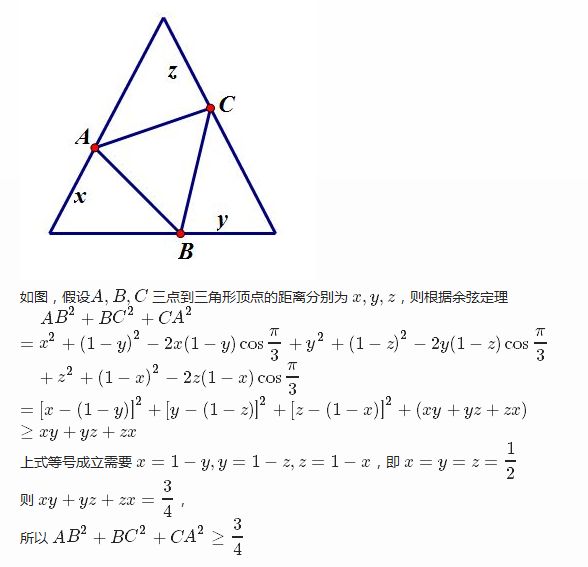
一、凸函数1、凸函数讲解设函数f(x)是定义在区间X上的函数,若对于区间上任意两点x1、x2和任意实数��∈(0,1),总有如下表达式成立:则称为f(x)是X上的凸函数;反之,如果下式成立:则称为f(x)在X上的凹函数。如图所示:Python实现凸函数:importnumpyasnpimportmatplotlib.pyplotasplt#定义凸函数defconvex_function(x):re
- 青少年编程与数学 01-012 通用应用软件简介 18 短视频平台
明月看潮生
编程与数学第01阶段青少年编程音视频编程与数学应用软件短视频
青少年编程与数学01-012通用应用软件简介18短视频平台一、什么是短视频平台(一)短视频平台的基本定义(二)短视频平台的工作原理(三)短视频平台的类型二、短视频平台的重要意义(一)为用户提供丰富的娱乐内容(二)推动数字内容创作的民主化(三)促进文化的传播与交流(四)提升用户互动性和社交性(五)推动数字经济的发展三、短视频平台主要产品(一)抖音1.软件功能2.特色3.市场地位和市场价值4.增值服务
- MATLAB算法实战应用案例精讲-【数模应用】主效应&交互效应&单独效应
林聪木
matlab算法开发语言
目录前言几个相关概念因素和水平主效应单纯主效应交互作用效应或影响(effect)因素之间的相互制约和影响两因素交互作用三因素及多因素交互作用几个高频面试题目什么是主效应,交互效应,单独效应?回归分析中是必须加入控制变量的吗?如果假如控制变量之后,显著性不高了该怎么办?控制变量说明控制变量选择控制变量处理主效应和交互效应的联系与区别如何依据主效应和交互效应描述结果?算法原理数学模型主效应二分变量交互
- Word 中批量转换 LaTeX 公式为标准数学格式的终极方法(附宏设置教程)
小灰兔的小白兔
wordc#开发语言
在学术写作中,我们常常需要将LaTeX格式的公式插入到Word文档中。但如果你有一大段公式使用$...$或LaTeX命令,手动转换无疑非常耗时。本文将介绍一种“一键转换所有LaTeX公式为Word数学公式”的方法,只需设置一次宏,后续即可像“格式刷”一样使用!原理简介MicrosoftWord实际上内置了对LaTeX的识别能力,但需要配合“公式编辑框”使用。借助宏(Macro)功能,我们可以批量触
- 【机器学习&深度学习】前馈神经网络(单隐藏层)
一叶千舟
深度学习【理论】机器学习深度学习神经网络
目录一、什么是前馈神经网络?二、数学表达式是什么?三、为什么需要“非线性函数”?四、NumPy实现前馈神经网络代码示例五、运行结果六、代码解析6.1初始化部分6.2前向传播6.3计算损失(Loss)6.4反向传播(手动)6.5更新参数(梯度下降)6.6循环训练七、训练过程可视化(思维图)八、关键问题答疑Q1:为什么需要隐藏层?Q2:ReLU是干嘛的?Q3:学习率怎么选?九、总结学习建议在机器学习中
- OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(SoftwareOpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速的环境或开发调试。例如在集成显卡HD620上运行SolidWorks时,若驱动不支持硬件加速,系统会自动回退到软件OpenGL模式(即"软件opengl")进行渲染。计算机图形学中也
- 《三生原理》如何解决长程依赖问题?
葫三生
三生学派人工智能平面线性代数概率论算法
AI辅助创作:《三生原理》通过融合《周易》的生成哲学与分形数学,创新性地重构了序列建模的逻辑框架,有效缓解长程依赖问题,其核心技术路径如下:一、八卦拓扑位置编码替代正弦编码符号系统的动态映射将伏羲八卦的拓扑结构(乾☰、坤☷等)转化为位置矩阵,通过模12余数配对法则建立位置关联性:阳爻(⚊)映射奇数位,阴爻(⚋)映射偶数位,形成周期性位置感知网格在512长度序列中,位置关系捕捉准确率提升2
- 随机近似算法:步长序列选择的理论与金融实践
随机近似算法:步长序列选择的理论与金融实践摘要随机近似算法作为统计学习与优化的核心工具,其收敛性与稳定性高度依赖步长序列的设计。本文系统阐述步长序列的理论约束与工程选择策略,并结合金融波动率估计场景,展示算法在动态系统参数估计中的实践价值。1.随机近似算法的数学框架随机近似算法通过随机样本的迭代更新逼近目标参数,其核心迭代式为:θn+1=θn+an(Yn−g(θn))\theta_{n+1}=\t
- 衡水中学状元数学学习资料完整攻略
向沙托夫问好
本文还有配套的精品资源,点击获取简介:《状元全科笔记衡水内部资料数学学习文档》提供了一个全面的数学学习资源,旨在通过衡水中学的教学经验和方法提升学生的数学成绩。资料包含基础知识、题型解析、模块训练、思维拓展和学习方法,引导学生深入理解数学概念,培养逻辑思维和解决问题的能力。文档结构清晰,内容详实,附带使用指南,帮助学生系统提升数学素养,实现学习效率和成绩的双重提高。1.状元学习方法分享在追求卓越成
- Linux的Initrd机制
被触发
linux
Linux 的 initrd 技术是一个非常普遍使用的机制,linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式,变化不仅反映在文件格式上, linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术,然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
- maven本地仓库路径修改
bitcarter
maven
默认maven本地仓库路径:C:\Users\Administrator\.m2
修改maven本地仓库路径方法:
1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml
2.找到
- XSD和XML中的命名空间
darrenzhu
xmlxsdschemanamespace命名空间
http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml
http://blog.csdn.net/wanghuan203/article/details/9203621
http://blog.csdn.net/wanghuan203/article/details/9204337
http://www.cn
- Java 求素数运算
周凡杨
java算法素数
网络上对求素数之解数不胜数,我在此总结归纳一下,同时对一些编码,加以改进,效率有成倍热提高。
第一种:
原理: 6N(+-)1法 任何一个自然数,总可以表示成为如下的形式之一: 6N,6N+1,6N+2,6N+3,6N+4,6N+5 (N=0,1,2,…)
- java 单例模式
g21121
java
想必单例模式大家都不会陌生,有如下两种方式来实现单例模式:
class Singleton {
private static Singleton instance=new Singleton();
private Singleton(){}
static Singleton getInstance() {
return instance;
}
- Linux下Mysql源码安装
510888780
mysql
1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz
(1)创建mysql的安装目录及数据库存放目录
解压缩下载的源码包,目录结构,特殊指定的目录除外:
- 32位和64位操作系统
墙头上一根草
32位和64位操作系统
32位和64位操作系统是指:CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的,但是这些CPU并不是真正意义上的64 位CPU,里面依然保留了大部分32位的技术,只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面,32位系统的最大寻址空间是2 的32次方= 4294967296(bit)= 4(GB)左右,而64位系统的最大寻址空间的寻址空间则达到了
- 我的spring学习笔记10-轻量级_Spring框架
aijuans
Spring 3
一、问题提问:
→ 请简单介绍一下什么是轻量级?
轻量级(Leightweight)是相对于一些重量级的容器来说的,比如Spring的核心是一个轻量级的容器,Spring的核心包在文件容量上只有不到1M大小,使用Spring核心包所需要的资源也是很少的,您甚至可以在小型设备中使用Spring。
- mongodb 环境搭建及简单CURD
antlove
WebInstallcurdNoSQLmongo
一 搭建mongodb环境
1. 在mongo官网下载mongodb
2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db"
3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
- 数据字典和动态视图
百合不是茶
oracle数据字典动态视图系统和对象权限
数据字典(data dictionary)是 Oracle 数据库的一个重要组成部分,这是一组用于记录数据库信息的只读(read-only)表。随着数据库的启动而启动,数据库关闭时数据字典也关闭 数据字典中包含
数据库中所有方案对象(schema object)的定义(包括表,视图,索引,簇,同义词,序列,过程,函数,包,触发器等等)
数据库为一
- 多线程编程一般规则
bijian1013
javathread多线程java多线程
如果两个工两个以上的线程都修改一个对象,那么把执行修改的方法定义为被同步的,如果对象更新影响到只读方法,那么只读方法也要定义成同步的。
不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据,就不要将方法设置为synchronized的。
- 将文件或目录拷贝到另一个Linux系统的命令scp
bijian1013
linuxunixscp
一.功能说明 scp就是security copy,用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议,保证了数据传输的安全,其格式如下: scp 远程用户名@IP地址:文件的绝对路径
- 【持久化框架MyBatis3五】MyBatis3一对多关联查询
bit1129
Mybatis3
以教员和课程为例介绍一对多关联关系,在这里认为一个教员可以叫多门课程,而一门课程只有1个教员教,这种关系在实际中不太常见,通过教员和课程是多对多的关系。
示例数据:
地址表:
CREATE TABLE ADDRESSES
(
ADDR_ID INT(11) NOT NULL AUTO_INCREMENT,
STREET VAR
- cookie状态判断引发的查找问题
bitcarter
formcgi
先说一下我们的业务背景:
1.前台将图片和文本通过form表单提交到后台,图片我们都做了base64的编码,并且前台图片进行了压缩
2.form中action是一个cgi服务
3.后台cgi服务同时供PC,H5,APP
4.后台cgi中调用公共的cookie状态判断方法(公共的,大家都用,几年了没有问题)
问题:(折腾两天。。。。)
1.PC端cgi服务正常调用,cookie判断没
- 通过Nginx,Tomcat访问日志(access log)记录请求耗时
ronin47
一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间
nginx.conf使用配置方式:
log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
- java-67- n个骰子的点数。 把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,打印出S的所有可能的值出现的概率。
bylijinnan
java
public class ProbabilityOfDice {
/**
* Q67 n个骰子的点数
* 把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,打印出S的所有可能的值出现的概率。
* 在以下求解过程中,我们把骰子看作是有序的。
* 例如当n=2时,我们认为(1,2)和(2,1)是两种不同的情况
*/
private stati
- 看别人的博客,觉得心情很好
Cb123456
博客心情
以为写博客,就是总结,就和日记一样吧,同时也在督促自己。今天看了好长时间博客:
职业规划:
http://www.iteye.com/blogs/subjects/zhiyeguihua
android学习:
1.http://byandby.i
- [JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析
comsci
工作流
我们已经不满足于仅仅跳跃一次,通过对引擎的升级,今天我测试了一下循环反馈模式,大概跑了200圈,引擎报一个溢出错误
在一个流程图的结束节点中嵌入一段方程,每次引擎运行到这个节点的时候,通过实时编译器GM模块,计算这个方程,计算结果与预设值进行比较,符合条件则跳跃到开始节点,继续新一轮拓扑分析,直到遇到
- JS常用的事件及方法
cwqcwqmax9
js
事件 描述
onactivate 当对象设置为活动元素时触发。
onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。
onbeforeactivate 对象要被设置为当前元素前立即触发。
onbeforecut 当选中区从文档中删除之前在源对象触发。
onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
- 正则表达式验证日期格式
dashuaifu
正则表达式IT其它java其它
正则表达式验证日期格式
function isDate(d){
var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i);
if(!v) {
this.focus();
return false;
}
}
<input value="2000-8-8" onblu
- Yii CModel.rules() 方法 、validate预定义完整列表、以及说说验证
dcj3sjt126com
yii
public array rules () {return} array 要调用 validate() 时应用的有效性规则。 返回属性的有效性规则。声明验证规则,应重写此方法。 每个规则是数组具有以下结构:array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
- UITextAttributeTextColor = deprecated in iOS 7.0
dcj3sjt126com
ios
In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0."
Ins
- 判断一个数是质数的几种方法
EmmaZhao
Mathpython
质数也叫素数,是只能被1和它本身整除的正整数,最小的质数是2,目前发现的最大的质数是p=2^57885161-1【注1】。
判断一个数是质数的最简单的方法如下:
def isPrime1(n):
for i in range(2, n):
if n % i == 0:
return False
return True
但是在上面的方法中有一些冗余的计算,所以
- SpringSecurity工作原理小解读
坏我一锅粥
SpringSecurity
SecurityContextPersistenceFilter
ConcurrentSessionFilter
WebAsyncManagerIntegrationFilter
HeaderWriterFilter
CsrfFilter
LogoutFilter
Use
- JS实现自适应宽度的Tag切换
ini
JavaScripthtmlWebcsshtml5
效果体验:http://hovertree.com/texiao/js/3.htm
该效果使用纯JavaScript代码,实现TAB页切换效果,TAB标签根据内容自适应宽度,点击TAB标签切换内容页。
HTML文件代码:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml"
- Hbase Rest API : 数据查询
kane_xie
RESThbase
hbase(hadoop)是用java编写的,有些语言(例如python)能够对它提供良好的支持,但也有很多语言使用起来并不是那么方便,比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口,它内嵌了jetty作为servlet容器。
启动命令:./bin/hbase rest s
- JQuery实现鼠标拖动元素移动位置(源码+注释)
明子健
jqueryjs源码拖动鼠标
欢迎讨论指正!
print.html代码:
<!DOCTYPE html>
<html>
<head>
<meta http-equiv=Content-Type content="text/html;charset=utf-8">
<title>发票打印</title>
&l
- Postgresql 连表更新字段语法 update
qifeifei
PostgreSQL
下面这段sql本来目的是想更新条件下的数据,可是这段sql却更新了整个表的数据。sql如下:
UPDATE tops_visa.visa_order
SET op_audit_abort_pass_date = now()
FROM
tops_visa.visa_order as t1
INNER JOIN tops_visa.visa_visitor as t2
ON t1.
- 将redis,memcache结合使用的方案?
tcrct
rediscache
公司架构上使用了阿里云的服务,由于阿里的kvstore收费相当高,打算自建,自建后就需要自己维护,所以就有了一个想法,针对kvstore(redis)及ocs(memcache)的特点,想自己开发一个cache层,将需要用到list,set,map等redis方法的继续使用redis来完成,将整条记录放在memcache下,即findbyid,save等时就memcache,其它就对应使用redi
- 开发中遇到的诡异的bug
wudixiaotie
bug
今天我们服务器组遇到个问题:
我们的服务是从Kafka里面取出数据,然后把offset存储到ssdb中,每个topic和partition都对应ssdb中不同的key,服务启动之后,每次kafka数据更新我们这边收到消息,然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了,最开始我们是在代码中打印存储的日志,发现没什么问题,后来去查看ssdb的日志,才发现里面每次set的时候都会对同一个key