Historically Highest Index algorithm HH-index算法

    算法课的ppt上看到一道习题，描述是这样的：

       In stock market, HH-index( historically highest ) of the current price isk means that current price it the highest price in the previousk days, but not the highest one in the previousk+1 days. Given the price of n days, please give an algorithm ofO(n) time complexity to calculate the HH-index of all days.

       简要地说，就是求数组每个元素在以它为起始向前能作为最大值的区间。初看这道题很容易，O(n²)的方法是不言自明的，而且似乎有很大提升空间。想出这个O(n)的算法也只需要一点小机巧，诡异的是我不知道怎么归类这个问题。

        具体思路是，假设给定的数组是price[n]，那么如果price[n] < price[n-1]，HH[n] = 1；如果price[n] =  price[n-1]，HH[n] = HH[n-1] +1；如果price[n] > price[n-1]，那么price[n]必然是HH[n-1]天内的最大值，但是不确定再之前的值，所以，只需要继续比较price[n]和price[n-HH[n-1]]的值就可以了（这一步比较关键！），然后可以重复这个过程。求HH[n]的过程用伪码来表示就是

 

HH-CALCULATE

for i ←1 to n

do   HH[i] ←1

if price[i] =price[i-1]

       then   HH[i] ←HH[i-1]

else if     price[i] > price[i-1]

       then    j ←i-1

while     j>0 andprice[i]>=price[j])

         do  HH[i]←HH[i] +HH[j]

                  j ← j-HH[j]

 

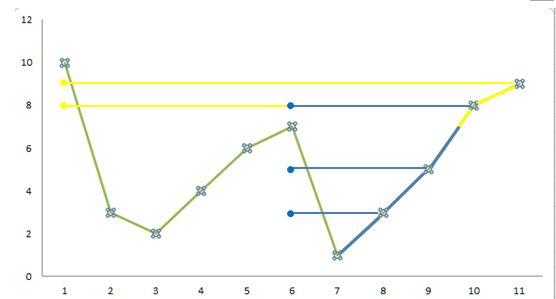
       复杂度分析：我只做了简单的形象化分析。把一个数组看成起起伏伏的波峰和波谷，于是这个数组就是由上坡过程和下坡过程组成的。那么显然在下坡过程中的点的比较次数很明显，都只有一次，总次数也就是下坡的长度。在上坡过程中，如图所示，圆点表示比较次数。从7到11的这个紫色上坡过程先是越过了6的波峰，比较次数为3，然后从11开始的黄色上坡过程就不会再与6的值比较。整个上坡过程的比较次数比上坡长度多了1，是由于10这个点翻越6时多比较了一次。归纳起来上坡过程的比较次数加起来也不会超过上坡的长度两倍（最多每个上坡都要翻越一次前面的波峰）。综上，总的比较次数必然少于2N。

        说这个问题不知道怎么归类是它这类似于一个DP问题（或者根本就是），某个问题（HH[n]）取决于一系列子问题（HH[i], i<n），然而需要用到哪些子问题却是不确定的，于是不太好用数学描述，这和其他DP问题有些不太一样。这个问题解决了，似乎求HL(historically lowest)也是顺理成章，只要将函数稍稍改下就可以了。这时候，我发现一道雅虎的笔试题真和这个问题很像，可惜当时没有思考过这道题，于是脑残地写了个O(n²)的算法，然后……就没然后了。

       这道题也是一个数组，还画成了一个柱状图，为了方便叙述，假设柱状图被染色了，要求能求出一个面积最大的有颜色的矩形。如图所示。

       容易想到的是检查以每个数组元素为高的最大矩形。这个矩形的宽度应该向左右尽量延伸，如第7个元素向左延伸2个单位，向右延伸1个单位。于是能得到n个矩形（如果有些元素高相等，就可能有重复）。符合要求的矩形就是这n个矩形中面积最大的。

       对于某个元素而言，这个矩形向左延伸的宽度等于HL，向右延伸的宽度，姑且定义为FL(futurely lowerst)吧，它和HL是一个几乎一样的问题：如果把这个数组颠倒，那么HL就成了FL，FL就成了HL。

        FL和HL都是一遍扫描就可以搞定的，甚至可以一遍同时搞定。面积比较也是再扫一遍的事情，于是结果就是O(2n)了。写了这几个函数的代码，没什么好说的了……（哎，我真搓！）

 #include <iostream>
 using namespace std;

 void printArray(int* , int);
 void getHH(int* , int, int*);
 void getHL(int* , int, int*);
 void getRect(int* , int, int*, int*);

 int main(){
 //  const int length = 10;
     int array[] = {1, 5, 3, 2, 8,
                      4, 3, 4, 1, 9};
     int length = sizeof(array)/sizeof(int);
     printArray(array, length);
     int HH[10], HL[10], FL[10];
     getHH(array, length, HH);
     getRect(array, length, HL, FL);
     return 1;

 }


 void printArray(int* array, int length){
     int max = 0;
     for(int i = 0; i < length; i++){
         max = (array[i] > max)?array[i]:max;
     }
     for(int i = max; i > 0; i--){
         for(int j = 0; j < length; j++){
             if(array[j] >= i){
                 cout<<"__  ";
             }else{
                 cout<<"    ";
             }
         }
         cout<<endl;
     }

 }

 void getHH(int* array, int length, int* HH){
     cout<<"i =     ";
     for(int i  = 0; i <  length; i++){
         cout<<i<<"  ";
     }
     cout<<"\nHH[i] = ";
     for(int i  = 0; i <  length; i++){
         HH[i]  = 1;
         while(i>=HH[i]&&array[i]>=array[i-HH[i]])
             HH[i] += HH[i-HH[i]];
         cout<<HH[i]<<"  ";
     }
     cout<<endl;
 }

 void getHL(int* array, int length, int* HL){
     int S = 0;
     int pre, last;
     for(int i  = 0; i <  length; i++){
         HL[i]  = 1;
         while(i>=HL[i]&&(array[i]<=array[i-HL[i]]))
             HL[i] += HL[i-HL[i]];
         if(array[i]*HL[i]>S){
             S = array[i]*HL[i];
             last = i;
             pre = last - HL[i];
         }
         //cout<<" i = "<<i<<" HL = "<<HL[i]<<endl;
     }
 }

 void getRect(int* array, int length, int* HL, int* FL){
     int S = 0;
     int start, end;

     for(int i  = 0; i <  length; i++){
         //scan the array to get HL and FL
         int i_rev = length-1-i;
         HL[i]  = FL[i_rev] = 1;

         while(i>=HL[i]&&(array[i]<=array[i-HL[i]]))
             HL[i] += HL[i-HL[i]];
         while(i>=FL[i_rev]&& (array[i_rev] <= array[i_rev + FL[i_rev]]))
             FL[i_rev] += FL[i_rev + FL[i_rev]];
     }

     for(int i = 0; i < length; i++){
         //find the rectangle
         cout<<"i = "<<i<<" HL = "<<HL[i]<<" FL = "<<FL[i]<<endl;
         if(array[i]*(HL[i]+FL[i]-1)>S){
             S = array[i]*(HL[i]+FL[i]-1);
             end = i + FL[i] -1;
             start =  i - HL[i] +1;
         }
     }

     cout<<"Rectangle's area is "<<S<<" and starts at "<<start<<" ends at "<<end<<endl;
     return;
 }