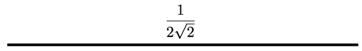小波变换网文精粹：小波变换和motion信号处理(十一)
小波变换网文精粹：小波变换和motion信号处理(十一)
转自：http://www.kunli.info/2011/02/18/fourier-wavelet-motion-signal-2/
（十一）scaling function与小波函数的结合
说到这里，可能你对scaling function以及多解析度分析已经比较理解了。但是，我们还没有涉及到它们在小波变换中的具体应用，也就是还没有回答刚才那个问题：凭空插了一个scaling function到小波basis组合中干嘛。也就是说，我们希望理解scaling function是怎么和小波函数结合的呢，多解析度能给小波变换带来什么样的好处呢。这其实就是是小波变换中的核心知识。理解了这个，后面的小波变换就是纯数学计算了。
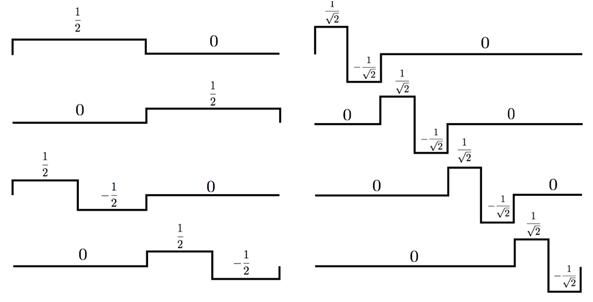
好，我们已经知道，对于子空间V0，basis是scaling function：
对应的小波函数是：
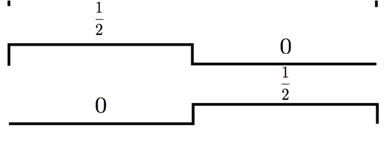
然后子空间V1的basis集合是这俩哥们：
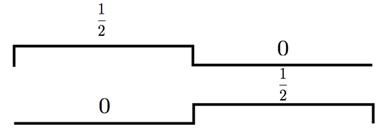
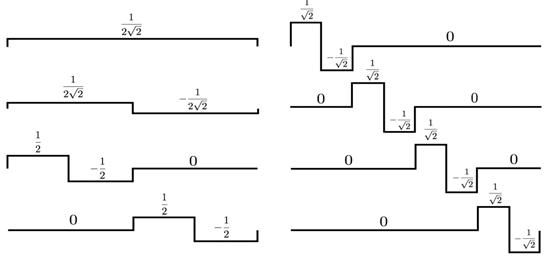
看出什么规律了么？多看几次这三个图，你会惊讶地发现，在V0中的scaling function和wavelet function的组合，其实就是V1中的basis！继续这样推导，V1本来的的basis是：
然后V1中对应的wavelet function是
他们的组合，本质上也就是V2的basis（参考图2）。你继续推导下去，会得到同样的结论：在scale j的wavelet function，可以被用来将Vj的basis扩展到V(j+1)中去！这是一个非常非常关键的性质，因为这代表着，对任何一个子空间Vj，我们现在有两种方法去得到它的orthonormal basis：
1. 一种就是它本来的basis ，对任意k。2. 第二种就是它上一个子空间的basis 
，对任意k，以及上一级子空间的wavelet function ，对任意k。
第二种选择能给我们带来额外的好处，那就是我们可以循环不断地用上一级子空间的scaling function以及wavelet function的组合来作为当前子空间的基。换句话说，如果针对V3这个子空间，它实际上就有四种不同的，但是等价的orthonormal basis：
1. 本级(V3)的scaling function basis set
2. 上一级(V2)的scaling function + wavelet function;
3 . 上上一级(V1)的scaling function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function;
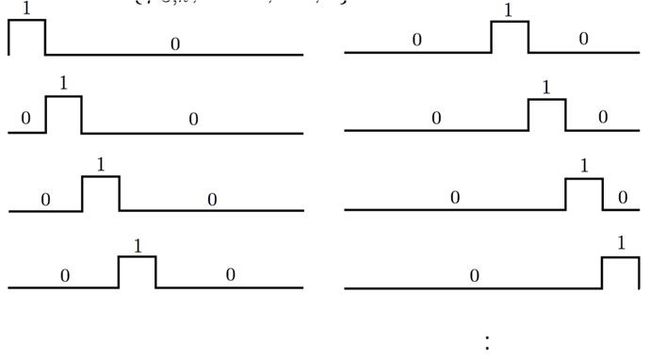
4. 上上上一级(V0)的scaling function + 上上上一级(V0)的wavelet function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function
好，看看最后一种选取方式，有没有感到眼熟？对了，它就是我们之前提到的“针对此信号space的哈尔小波basis组合”，参见图1。现在我们知道了，这个scaling function不是凭空插进去的，而是通过不断的嵌套迭代出来的：）