dp+四边形不等式优化(poj1160 hdu2829 3480 3506 3516)
一、四边形不等式基本理论
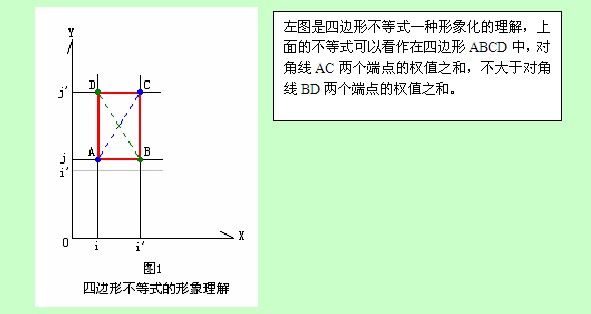
在动态规划的转移方程中,常见这样一种转移方程:
这两个定理证明在赵爽的《动态规划加速原理之四边形不等式》中给出了相关的证明。
二、四边形定理的应用
1、poj1160 题目大意:给定n个城市,在m个城市里建邮局,使所有城市到最近邮局的距离和最小。很容易得到这样的方程:
dp(i,j)=min(dp(i-1,k)+w(k+1,j)) , i-1<=k<j s(i-1,j)<=k<=s(i,j+1)
w(i,j)=w(i,j-1)+val[j]-val[(j+i)/2] , i<j<=n
dp(1,i)=w(1,i), w(i,i)=0, s(1,i)=0
对于函数w(i,j)有人可能疑问,从i到j建一座邮局,对于邮局位置k,(i<=k<=j),这是一个凹区间,k选在i ,j的中间位置w(i,j)才是最小的,如何j-i是一个奇数,那么中间的两个数都是距离最小的点。对于w满足四边形不等式和区间单调性(本人表示不大会证,一般动态转移方程类似,n^3不能解决的问题,都是这么搞吧)。于是,我们限制了原方程中k的取值范围,得到了O(n^2)算法。
#include <iostream>
#include <cstdio>
using namespace std;
#define inf 0x7ffffff
#define MIN(a,b) ((a)<(b)?(a):(b))
int dp[31][301];
int val[301];
int w[301][301];
int s[31][301];//表示前i-1个邮局的城市数
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;++i)
{
scanf("%d",&val[i]);
}
for(int i=1;i<=n;++i)
{
w[i][i]=0;
for(int j=i+1;j<=n;++j)
{
w[i][j]=w[i][j-1]+val[j]-val[(i+j)/2];
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
dp[j][i]=inf;
}
}
for(int i=1;i<=n;++i)
{
dp[1][i]=w[1][i];
s[1][i]=0;
}
for(int i=2;i<=m;++i)
{
s[i][n+1]=n;
for(int j=n;j>i;--j)
{
for(int k=s[i-1][j];k<=s[i][j+1];++k)
{
if(dp[i-1][k]+w[k+1][j]<dp[i][j])
{
s[i][j]=k;
}
dp[i][j]=MIN(dp[i][j],dp[i-1][k]+w[k+1][j]);
}
}
}
printf("%d\n",dp[m][n]);
}
return 0;
}
2、hdu2829题目大意:给定一个长度为n的序列,至多将序列分成m段,每段序列都有权值,权值为序列内两个数两两相乘之和。m<=n<=1000. 令权值最小。
状态转移方程很好想,dp[i][j] = min(dp[i][j],dp[i-1][k]+w[k+1][j])(1<=k<i)
通写法是n*n*m,当n为1000时运算量为10亿级别,必须优化。
四边形不等式优化,主要是减少枚举k的次数。w[i][j]是某段区间的权值,当区间变大,权值也随之变大,区间变小,权值也随之变小,此时就可以用四边形不等式优化。
我们设s[i][j]为dp[i][j]的前导状态,即:dp[i][j]=dp[i-1][s[i][j]]+ w[s[i][j]+1][j].之后我们枚举k的时候只要枚举s[i-1][j]<=k<=s[i][j+1],此时i必须从小到大遍历,j必须从大到小
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define min(a,b) ((a)<(b)?(a):(b))
#define LL long long
#define inf (LL)1<<60
LL dp[1002][1002];
LL w[1002][1002];
LL s[1002][1002];
LL p[1002];
LL val[1002][1002];
int main()
{
int m,n;
while(~scanf("%d%d",&n,&m))
{
if(!n&&!m)break;
for(int i=1;i<=n;++i)
{
scanf("%lld",&p[i]);
}
memset(dp,0,sizeof(dp));
memset(w,0,sizeof(w));
memset(val,0,sizeof(val));
for(int i=1;i<n;++i)
{
for(int j=i+1;j<=n;++j)
{
val[i][j]=val[i][j-1]+p[i]*p[j];
}
}
for(int i=n-1;i>=1;--i)
{
for(int j=i+1;j<=n;++j)
{
w[i][j]=w[i+1][j]+val[i][j];
}
}
for(int i=1;i<=m+1;i++)
{
for(int j=i+1;j<=n;++j)
{
dp[i][j]=inf;
}
}
for(int i=1;i<=n;++i)
{
dp[1][i]=w[1][i];
s[1][i]=0;
}
for(int i=2;i<=m+1;++i)
{
s[i][n+1]=n;
for(int j=n;j>i;--j)
{
for(int k=s[i-1][j];k<=s[i][j+1];++k)
{
LL tmp=dp[i-1][k]+w[k+1][j];
// cout<<i<<' '<<j<<' '<<k<<' '<<tmp<<endl;
if(tmp<dp[i][j])
{
dp[i][j]=tmp;
s[i][j]=k;
}
}
}
}
if(m+1>=n){dp[m+1][n]=0;}
printf("%lld\n",dp[m+1][n]);
}
3、hdu3480 题目大意:给出n个数字,要你把这n个数字分成m堆,每一堆的价值是(max(val) - min(val)) ^ 2 要你求出分成m堆之后得到的最小价值
设dp[i][j]表示前j个数字,分成i堆的最小价值。分析得到,当i<j<k<l,val[i] < val[j] < val[k] < val[l]的话,能得到最优值 因此先排序,然后容易得到式子dp[i][j] = min(dp[i - 1][k] + (val[j] - val[k + 1]) ^ 2) 这条就是典型的符合单调性的转移方程 因此直接套四边形不等式就可以解决了
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define LL long long
#define inf 0x6fffffff
int dp[5002][10002];
int p[10002];
int s[5002][10002];
int cmp(const void *a,const void *b)
{
return *(int*)a-*(int*)b;
}
int main()
{
int cas,m,n,c;
while(~scanf("%d",&cas))
{
c=1;
while(cas--)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{
scanf("%d",&p[i]);
}
qsort(p+1,n,sizeof(p[0]),cmp);
memset(s,0,sizeof(s));
for(int i=1;i<=m;++i)
{
for(int j=i;j<=n;++j)
{
if(j<=i){dp[i][j]=0;}
else {dp[i][j]=inf;}
}
}
for(int i=1;i<=n;++i)
{
s[1][i]=0;
dp[1][i]=(p[i]-p[1])*(p[i]-p[1]);
}
for(int i=2;i<=m;++i)
{
s[i][n+1]=n;
for(int j=n;j>i;--j)
{
for(int k=s[i-1][j];k<=s[i][j+1];++k)
{
int tmp=dp[i-1][k]+(p[j]-p[k+1])*(p[j]-p[k+1]);
if(tmp<dp[i][j])
{
dp[i][j]=tmp;
s[i][j]=k;
}
}
}
}
printf("Case %d: %d\n",c++,dp[m][n]);
}
}
return 0;
}
4、hdu3516 题目大意:给你很多个点,让你用一棵树把所有点连在一齐,树只能往上跟右生长,求树的总长度最小。
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
#define min(a,b) ((a)<(b)?(a):(b))
#define inf 0x7ffffff
struct point{
int x,y;
};
point p[1000];
int dp[1000][1000];
int s[1000][1000];
int w[1000][1000];
int getdis(point a,point b)
{
return abs(a.x-b.x)+abs(a.y-b.y);
}
int main()
{
int n;
while(~scanf("%d",&n))
{
for(int i=1;i<=n;++i)
{
scanf("%d%d",&p[i].x,&p[i].y);
}
for(int i=1;i<n;++i)
{
for(int j=i+1;j<=n;++j)
{
w[i][j]=getdis(p[i],p[j]);
}
s[i][i+1]=i;
dp[i][i+1]=w[i][i+1];
}
for(int len=3;len<=n;++len)
{
for(int i=1;i<=n-len+1;++i)
{
int j=i+len-1;
dp[i][j]=inf;
for(int k=s[i][j-1];k<=s[i+1][j];++k)
{
int tmp=dp[i][k]+dp[k+1][j]+w[i][j]+p[k].y-p[i].y+p[k+1].x-p[j].x;
//cout<<i<<' '<<j<<' '<<k<<' '<<tmp<<endl;
if(tmp<dp[i][j])
{
dp[i][j]=tmp;
s[i][j]=k;
}
}
}
}
printf("%d\n",dp[1][n]);
}
return 0;
}
5、hdu3506 题目大意:香蕉森林里一群猴子(n<=1000)围成一圈开会,会长给他们互相介绍,每个猴子需要时间a[i]。每次只能介绍相邻的两只猴子x和y认识,同时x所有认识的猴子和y所有认识的猴子也就相互认识了,代价为这两伙猴子认识的时间(a[i])之和。求这群猴子都互相认识的最短时间。
这道题其实就是环形的石子合并问题,首先将环形dp转化为线性dp,对于长度为n的环,任意选取一点为起点,由起点开始得到一条长度为n的链,将前面n-1长度的链复制并转移到链的末端,相当于将两条同样的链首尾相接。这样环的任意一种单向遍历方式都可以在这个长度这为2n-1的链中实现。可见曾妞妞的《怎样实现环形动态规划问题》。
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
#define LL int
#define inf 1<<30
#define min(a,b) ((a)<(b)?(a):(b))
LL dp[2002][2002];
LL s[2002][2002];
LL p[2002];
LL w[2002][2002];
int main()
{
int n;
while(~scanf("%d",&n))
{
for(int i=1;i<=n;++i)
{
scanf("%d",&p[i]);
p[i+n]=p[i];
}
memset(s,0,sizeof(s));
memset(w,0,sizeof(w));
for(int i=1;i<2*n;++i)
{
for(int j=i;j<=i+n;++j)
{
w[i][j]=w[i][j-1]+p[j];
}
s[i][i]=i;
dp[i][i]=0;
}
for(int len=2;len<=n;++len)
{
for(int i=1;i<=2*n-len+1;++i)
{
int j=i+len-1;
dp[i][j]=inf;
for(int k=s[i][j-1];k<=s[i+1][j];++k)
{
LL tmp=dp[i][k]+dp[k+1][j]+w[i][j];
if(tmp<dp[i][j])
{
dp[i][j]=tmp;
s[i][j]=k;
}
}
}
}
LL ans=inf;
for(int i=1;i<=n;++i)
{
ans=min(ans,dp[i][i+n-1]);
}
printf("%d\n",ans);
}
return 0;
}