拓扑排序的c语言实现
以下的介绍是百度上的,因为这个实在太老了。但是只是单纯自己的一个程序显得不是很完整的。呵呵
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。离散数学中关于偏序和全序的定义:
若集合X上的关系是R是自反的、反对称的和传递的,则称R是集合X上的偏序关系。
设R是集合X上的偏序(Partial Order),如果对每个x,y属于X必有xRy 或 yRx,则称R是集合X上的全序关系。
注意:
①若将图中顶点按拓扑次序排成一行,则图中所有的有向边均是从左指向右的。
②若图中存在有向环,则不可能使顶点满足拓扑次序。
③一个DAG的拓扑序列通常表示某种方案切实可行。
实现的基本方法
拓扑排序方法如下:
(1)从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它.
(2)从网中删去该顶点,并且删去从该顶点发出的全部有向边.
(3)重复上述两步,直到剩余的网中不再存在没有前趋的顶点为止.
//本程序用的是邻接矩阵的方法计算拓扑排序的。
#include<stdio.h>
#define N 6//这是代表了 节点的个数
void Topologicalsort(int matrix[][N]);
//以下几个是简单的堆栈函数因为文中要用到。
void initstack(int*stack,int*n)
{
for(int i=0;i<*n+1;i++)
stack[i]=-1;
*n=0;
}
void push(int*stack,int *n,int elem)
{
stack[*n]=elem;
(*n)++;
}
int pop(int*stack,int *n)
{
int temp;
(*n)--;
temp=stack[*n] ;
stack[*n]=-1;
return temp;
}
int isempty(int*stack,int *n)
{
if(*n)
return 0;
return 1;
}
int main()
{
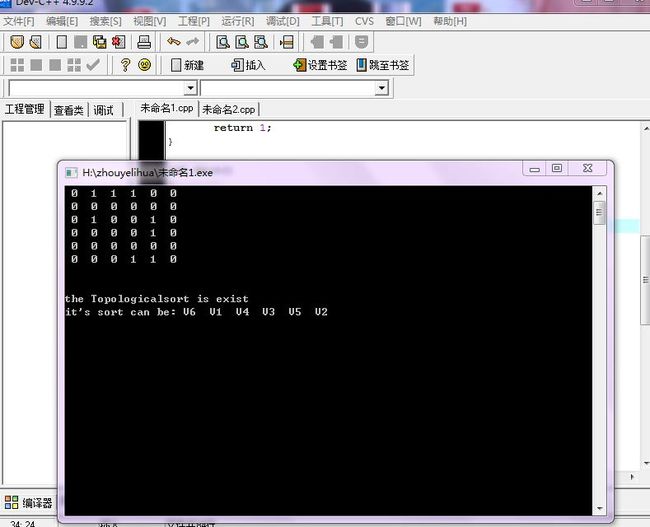
int matrix[N][N]={{0,1,1,1,0,0},
{0,0,0,0,0,0},
{0,1,0,0,1,0},
{0,0,0,0,1,0},
{0,0,0,0,0,0},
{0,0,0,1,1,0}}; //初始化邻接矩阵。
for(int i=0;i<N;i++){
for(int j=0;j<N;j++)
printf(" %d ",matrix[i][j]);
printf("\n");}//打印矩阵
Topologicalsort(matrix);
getchar();
return 0;
}
//拓扑排序函数
void Topologicalsort(int matrix[][N])
{
int indegree[N]={0};//入度矩阵
int sortorder[N]={0};//这是用于存放最后的拓扑排序 的序列
int sortordercurse=0;
int stack[N+1];
int curse=N+1;
initstack(stack,&curse);
int count=0;//用来指示入度为0的顶点个数
for(int j=0;j<N;j++){
for(int i=0;i<N;i++)
indegree[j]+=matrix[i][j];
if(!(indegree[j]))
push(stack,&curse,j); } //入度为0的顶点入栈
while(!(isempty(stack,&curse)))
{
int tp;
tp=pop(stack,&curse);
sortorder[sortordercurse++]=tp;
count++;
for(int i=0;i<N;i++){
if((indegree[i]==1)&&(matrix[tp][i]==1))
push(stack,&curse,i);
indegree[i]-=matrix[tp][i];}//对出栈的顶点所指向的顶点减一 ,并且将入度为0的顶点入栈。
}
if(count==N){
printf("\n\nthe Topologicalsort is exist\nit's sort can be:");
for(int i=0;i<sortordercurse;i++)
printf(" V%d ",sortorder[i]+1);}
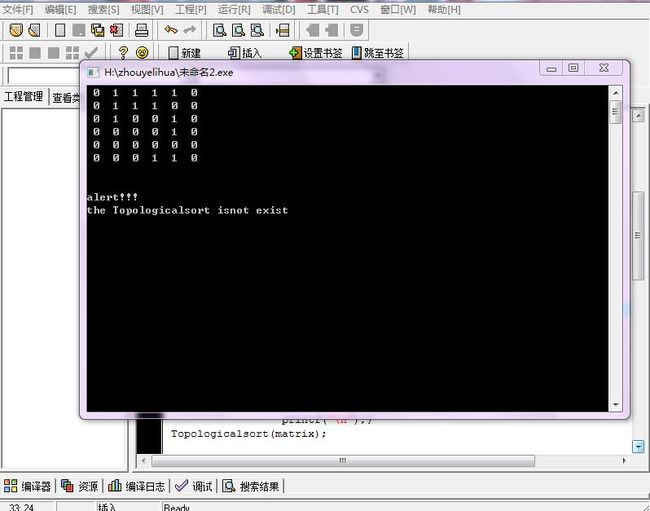
else{
printf("\n\nalert!!!\nthe Topologicalsort isnot exist\n");} //判断是否是拓扑排序。
}