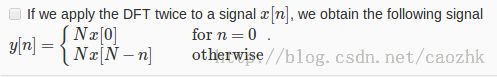向量空间中的Fourier变换：DFT DFS DTFT

DFT

持久的动态系统一定存在振荡现象。从直观理解来说，不沿着圆运动的物体终将停止，比如炸弹、人、火箭等不可逆转的事物。

对于有限长度的一段信号，如64点。Wk[n]=e^(j*2*pi/N*n*k),n,k在【0，1，……N-1】，为C64向量空间的一组正交基。任取两个不同的基计算内积，化简为等比数列求和，分子为0，即正交。不过它们不是标准正交，乘以1/sqrt(N)标准化因子后才是标准正交基。

Wk表示第k个向量。每个Wk可以视为在一个园周上的逆时针运动，整个64长度时间轴上总共移动了k个园周。W0为常量，W2每次移动2*pi/N*2，W16每次移动pi/4，k在16和32之间移动会造成cos和sin波形不易看懂。大于32时，每次移动超过pi/2，相当于逆时针移动的W(64-k)，cos相同，但sin是负的。

对信号x分析的时候，可以不加以标准化，直接计算与正交基的内积，得到Xk。由这些分量综合出x的时候，需要乘以1/N以标准化：x=1/N * sum(Xk * Wk)。注意A、B内积的计算方法为A* xB，前者要取共扼。内积表示两个信号之间的相似程度。

Fourier变换可以看作从一组时域冲击信号正交基到Wk正交基的基变换。由于是计算内积，那么变换矩阵的因子为（e(-j*2*pi/N)）.

上述即为DFT，离散Fourier变换。实信号的幅度是关于中心对称的。（猜测虚部应该是奇对称的。）如果信号是前后部分虚部相同，实部反号，则DFT的实部为0.

这个结论采用两个Fourier变换矩阵W相乘可以得到结果。

如果以48k采样，那么36k的噪声会在12k频率处产生分量，60k的噪声也会在12k频率处产生分量。这里的产生分量的意思是滤波无法把噪声滤除。这一点可以用在园周上的旋转来理解，也可以用采样频率过低造成频谱泄漏来理解。

Parseval， 一个向量的能量等于它在一组标准正交基上的分量的幅度的平方和。进而得到DFT下的形式。

DFS

对于周期性的信号，取一个周期进行DFT即可，多个周期只会在频域插0.

DTFT

对于无限长的离散时间的非周期信号，要采用DTFT。假设信号是能量有限的。

频谱是2*pi周期性的。

变换特性：DTFT(x[-n]) = X(e^ (-j*w) ) DTFT( x*[n] ) = X* (e^ (-j*w))。

冲击函数的频域均为1.

全是1的函数DFFT是周期的幅度为2*pi的冲击函数。

还有：

DTFT的计算：

三者的关系

对于有限长信号序列，可以前后补零扩展为无限长序列，亦可周期扩展。

周期扩展后的信号的DTFT与原信号的DFT类似，但幅度变为了X[k]*delta。即冲击。

补零扩展后的DTFT相当于原信号的DFT的每一个点都变为一个sinc函数，即频谱变为连续的。

有限长序列后方补零，对应的DFT相当于对补零扩展后的DTFT的采样，也可以理解为插值，但没有带来信息。

FFT

长度为N的DFT的结果可以分为奇数和偶数部分来计算，得到的是x【n】的奇数部分和偶数部分分别做FFT，后者乘以Wn ^ k，两部分加减记得。

N=8时的流程图如下：

可以看到整个流程中的乘法因子始终是WN，而不是W4，W2，比较费解。

快速实现的C语言库有 FFTW