poj 1556 &zoj 1721
The Doors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5258 | Accepted: 2140 |
Description
You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length.
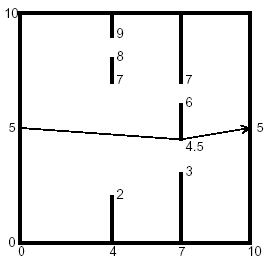

Input
The input data for the illustrated chamber would appear as follows.
2
4 2 7 8 9
7 3 4.5 6 7
The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1.
2
4 2 7 8 9
7 3 4.5 6 7
The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1.
Output
The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.
Sample Input
1 5 4 6 7 8 2 4 2 7 8 9 7 3 4.5 6 7 -1
Sample Output
10.00 10.06
这是一道计算几何和最短路结合的题目,题目的关键就在于如何建图,说来我对计算几何一窍不通,只有在观摩了大贴后,也只是略知一二。下面是代码:
#include <iostream> #include <cmath> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #define eps 1e-8 #define inf 100000000 using namespace std; struct Wall{ double x; double y[6]; }wall[20]; double dist[80][80]; double xmult(double x0,double y0,double x1,double y1,double x2,double y2){ return (x1-x0)*(y2-y0)-(x2-x0)*(y1-y0); } int dblcmp( double a ){ if( fabs(a)< eps ) return 0; return (a>0)?1:-1; } bool Cross( double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3 ){//判断两条直线是否相交 return (dblcmp(xmult(x0,y0,x2,y2,x3,y3))^dblcmp(xmult(x1,y1,x2,y2,x3,y3)))==-2 && (dblcmp(xmult(x2,y2,x0,y0,x1,y1))^dblcmp(xmult(x3,y3,x0,y0,x1,y1)))==-2; } bool Direct( int i, int j, int p, int q ){ //判断从墙i的第j个点到墙p第q个点是否直达 int k, l; for( k= i+1; k< p; k++ ){ for( l= 0; l< 6; l+= 2 ) if( Cross(wall[i].x,wall[i].y[j],wall[p].x,wall[p].y[q], wall[k].x,wall[k].y[l],wall[k].x,wall[k].y[l+1]) ) return false; } return true; } inline double Dist( double x1, double y1, double x2, double y2 ){ return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); }; typedef double elem_t; double dijkstra(int n){ int v[81],i,j,k; double min[81]; for (i=0;i<=n;i++) min[i]=inf,v[i]=0; for (min[0]=0,j=0;j<=n;j++){ for (k=-1,i=0;i<=n;i++) if (!v[i]&&(k==-1||min[i]<min[k])) k=i; for (v[k]=1,i=0;i<=n;i++) if (!v[i]&&min[k]+dist[k][i]<min[i]) min[i]=min[k]+dist[k][i]; } return min[n]; } int main(){ int n, i, j, k, l; wall[0].x= 0; wall[0].y[0]= 5; while( scanf("%d",&n) && n!=-1 ){ for( i= 0; i<= n*4+1; i++ ) for( j= 0; j<= n*4+1; j++ ) dist[i][j]= inf; wall[n+1].x= 10; wall[n+1].y[1]= 5; bool con= true; for( i= 1; i<= n; i++ ){ scanf("%lf",&wall[i].x); for( j= 1; j< 5; j++ ) scanf("%lf",&wall[i].y[j]); if( wall[i].y[1]>5 || wall[i].y[4]<5 || wall[i].y[2]<5&&wall[i].y[3]>5 ) con= false; wall[i].y[0]= 0; wall[i].y[5]= 10; } if( con ){ puts("10.00"); continue; } for( i= 1; i<= n; i++ ){ for( j= 1; j< 5; j++ ){ if( i< n ) for( k= 1; k< 5; k++ ) dist[i*4+j-4][i*4+k]= Dist(wall[i].x,wall[i].y[j],wall[i+1].x,wall[i+1].y[k]); if( Direct( 0, 0, i, j ) ) dist[0][i*4+j-4]= Dist(0,5,wall[i].x,wall[i].y[j]); if( Direct( i, j, n+1, 1 ) ) dist[i*4+j-4][n*4+1]= Dist(wall[i].x,wall[i].y[j],10,5); for( k= i+2; k<= n; k++ ) for( l= 1; l< 5; l++ ) if( Direct(i,j,k,l) ) dist[i*4+j-4][k*4+l-4]= Dist(wall[i].x,wall[i].y[j],wall[k].x,wall[k].y[l]); } } printf("%.2lf\n",dijkstra(n*4+1)); } return 0; }