游戏中的三角学——Sprite Kit 和 Swift 教程（2）

• 原文链接 : Trigonometry for Games – Sprite Kit and Swift Tutorial: Part 2/2
• 原文作者 : Nick Lockwood
• 译文出自 : 开发技术前线 www.devtf.cn
• 译者 : kmyhy

游戏编程中的三角学！

2015年4月20日 更新：更新到 Xcode 6.3 和 Swift 1.2。

更新说明：这是我们广受欢迎的教程之一的第三个版本——第一个版本是 Cocos2D 的，由 Matthijs Hollemans 缩写，第二个版本由 Tony Dahbura 升级为 Sprite Kit。最终的版本仍然是 Sprite Kit 的，但升级至 iOS 8 和 Swift。

欢迎回到游戏编程中的三角学系列！

在这个系列的第一部分，我们学习了基本的三角学知识，它在游戏制作中是非常有用的。数学并不令人讨厌——尤其当你将它放到一个充满趣味的项目中！

在第二部分，我们会在这个简单的飞行游戏中加入导弹，一个轨道式卫星护盾以及一个写着的“游戏结束”的动画界面。在这个过程中，你将学习 sin 和 cos 函数，以及其它在游戏中用得到的三角学工具。

准备乘上正弦波的快车，回到太空吧！

开始

这个教程和上一部分的内容一脉相承。如果你还没有看过第一部分，你可以从这里下载第一部分的源代码。

目前，在游戏中有一艘飞船、一座旋转炮台，它们都会有血槽显示。它们是不共戴天的仇敌，但谁也不能把谁怎么样，除非飞船硬要撞到炮台上（炮台的损失要相对好一点）。

是时候放点烟火了。我们将增加一个功能，让玩家通过划动屏幕来发射导弹。划动的发现就是导弹发射的方向。要记录用户触摸，我们需要增加新的属性。

打开 GameScene.swift ，然后添加如下属性：

let playerMissileSprite = SKSpriteNode(imageNamed:"PlayerMissile")

var touchLocation = CGPointZero
var touchTime: CFTimeInterval = 0

我们将从飞船前进的方向开始移动导弹。我们用 touchLocation 和 touchTime 记录用户触摸的位置和时间，以便发射导弹。

然后，在 didMoveToView() 方法底部加入几行：

playerMissileSprite.hidden = true
addChild(playerMissileSprite)

注意，导弹一开始是隐藏的，只有玩家发射它之后才可见。为了降低难度，玩家一次只能发射一颗导弹。

首先添加第一个触摸事件处理方法 touchesBegan()。这个方法会在用户将手指放到屏幕上之后调用：

override func touchesBegan(touches: Set<NSObject>, withEvent event: UIEvent) {

  if let touch = touches.first as? UITouch {

    let location = touch.locationInNode(self)
    touchLocation = location
    touchTime = CACurrentMediaTime()
  }
}

非常简单——当触摸被检测到，保存当前触摸的位置和时间。真正的工作放到 touchesEnded() 方法中进行：

override func touchesEnded(touches: Set<NSObject>, withEvent event: UIEvent) {

  let TouchTimeThreshold: CFTimeInterval = 0.3
  let TouchDistanceThreshold: CGFloat = 4

  if CACurrentMediaTime() - touchTime < TouchTimeThreshold && playerMissileSprite.hidden {

    if let touch = touches.first as? UITouch {

      let location = touch.locationInNode(self)
      let swipe = CGVector(dx: location.x - touchLocation.x, dy: location.y - touchLocation.y)
      let swipeLength = sqrt(swipe.dx * swipe.dx + swipe.dy * swipe.dy)
      if swipeLength > TouchDistanceThreshold {
        // TODO: more code here
      }
    }
  }
}

外层的 If 语句计算从扫动开始到结束的时间差。如果这个时间差大于 TouchTimeThreshold 值（0.3秒），导弹将被发射。同时，因为玩家一次只能发射一个导弹，如果导弹还在飞行中，则触摸被忽略。

接下来计算用户在做什么手势，是轻扫，还是轻击？只有在轻扫的时候才应该发射导弹，而不是轻击。我们花了一点时间来计算这个——将两个位置相减，然后用勾股定理计算它们之间的距离。如果距离大于 TouchDistanceThreshold(4 point)，则认为用户想轻扫。

注意：在 UIKit 中有内置的轻扫手势识别器，但我们的教程是学习三角学知识，因此这里用这种方式来识别。

要让导弹飞起来有两种方式：

第一种方式是创建一个 playerMissileVelocity 向量，根据你瞄准的方向来创建。在update() 方法中，我们可以在每一帧将这个速度（乘以时间差）施加到导弹精灵上，然后判断导弹是否飞出了屏幕边沿以外，以便让导弹重置。这就好比第一部分中我们让飞船移动的方式。

但和飞船不同，导弹是不需要改变飞行方向的，它成直线飞行。因此我们可以用一个更简单的方法：第二种方式是导弹发射后，计算导弹的终点。然后用 moveTo() 动作，让 Sprite Kit 将它以动画方式移动到终点。

这种方式不需要我们判断导弹是否在屏幕可视区域内，同时也可以做一些更有趣的数学题！

首先，将 touchesEnded() 方法中 // TODO 注释替换为：

var angle = atan2(swipe.dy, swipe.dx)
playerMissileSprite.zRotation = angle - 90 * DegreesToRadians

playerMissileSprite.position = playerSprite.position
playerMissileSprite.hidden = false

这里我们使用 atan2() 将 swipe 向量转换为角度，然后设置精灵的角度和位置，让导弹不再隐藏。

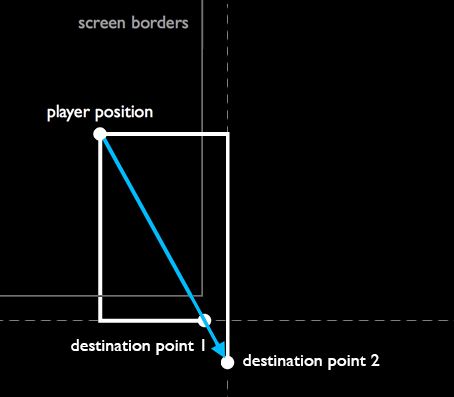
然后是好玩的地方了。我们知道导弹的开始位置（玩家飞船的当前位置），也知道角度（来自于玩家扫动动作）。我们需要算出终点。

我们有了方向向量，从第一部分中学到如何用规范化将向量的长度设置为指定长度。但我们怎么知道这个长度是多少？这个问题问得好：因为我们想让导弹一移到屏幕以外就停下来，这个长度应该取决于起点和方向。

终点是在屏幕以外，而不是整好屏幕的边缘，因为要让导弹完全飞出屏幕才能让它消失。因此，在GameScene.swift 中增加一个常量：

let PlayerMissileRadius: CGFloat = 20

终点的计算有点复杂。如果你知道（假设）玩家正在朝下射击，你可以算出导弹需要飞行的垂直距离——导弹起点的 Y 坐标，加上 PlayerMissileRaius，但是我们同时还要根据导弹在哪里和可视边界相交来算出 X 坐标。

对于飞出屏幕顶部或底部的导弹，终点的 x 坐标可以用下面的公式来计算：

destination.x = playerPos.x + ((destination.y – playerPos.y) / swipe.dy * swipe.dx)

这和第一部分教程中的规范化类似，先将两个直角边除以长度，在乘以需要的长度。这里，先用 swipe.y 组件与最终距离的 y 相除算出一个系数，然后用这个系数乘以 scale.x (即算出三角形的对边)，然后加上飞船的 x 坐标，得到终点的 x 坐标。

如果导弹从左边或右边飞出屏幕，我们可以使用同样的公式，但 x 和 y 值要调换一下。这种将一个向量拉伸到某个边界的技术，被称作“投影”，它对于所有类型的游戏都非常有用，比如要判断敌人是否能够看到玩家时，就可以将一个向量沿敌人的视线进行投影，一直投射到某堵墙或者玩家。

但是这种技术有一点问题。如果交点是一个角（或角的附近），则不好判定是哪一边先发生相交：

很简单，你可以同时计算两个交点，看哪一个更短！

在 touchesEnded 方法的 playerMissileSprite.hidden = false 一句下面加入：

//calculate vertical intersection point
var destination1 = CGPoint.zeroPoint
if swipe.dy > 0 {
  destination1.y = size.height + PlayerMissileRadius // top of screen
} else {
  destination1.y = -PlayerMissileRadius // bottom of screen
}
destination1.x = playerSprite.position.x +
  ((destination1.y - playerSprite.position.y) / swipe.dy * swipe.dx)

//calculate horizontal intersection point
var destination2 = CGPoint.zeroPoint
if swipe.dx > 0 {
  destination2.x = size.width + PlayerMissileRadius // right of screen
} else {
  destination2.x = -PlayerMissileRadius // left of screen
}
destination2.y = playerSprite.position.y +
  ((destination2.x - playerSprite.position.x) / swipe.dx * swipe.dy)

这里，我们计算了俩个交点，我们要找出哪个交点距离玩家更近。因此，在上一段代码之后，紧接着用下面的代码进行判断：

// find out which is nearer
var destination = destination2
if abs(destination1.x) < abs(destination2.x) || abs(destination1.y) < abs(destination2.y) {
  destination = destination1
}

你可以用勾股定理算出从玩家到每个交点的对角线距离，然后选择最短的。但还有一个更快的方法：我们知道两个交点都位于同一个向量，则只要点的 x 或者 y 两者中有一个比对方短，则它的长度也应该是较短的——其实并不需要计算对角线长度。

现在开始发射导弹！
在 touchesEnded() 方法中，紧接着上一段代码之后，加入：

// run the sequence of actions for the firing
let missileMoveAction = SKAction.moveTo(destination, duration: 2)
playerMissileSprite.runAction(missileMoveAction) {
  self.playerMissileSprite.hidden = true
}

运行程序，轻扫向炮台开火。很好。注意你一次只能发射一枚导弹——要等上一枚导弹消失，才能再次开火。

还有一个问题（就知道是这样!）——导弹的速度会根据它飞行的距离变化。那是因为当前动画时长是硬编码的（2秒）。导弹飞得越远，当然就速度越快，这样才能在同样的时间下飞过更远的距离嘛。如果导弹以匀速飞行好像更理想一点。

你的好朋友艾萨克.牛顿又来帮忙了！牛顿发明了“时间 = 距离/速度”公式。你可以通过勾股定律算出距离，因此问题就只剩下指定一个速度了。

在 GameScene.swift 头部加入常量：

let PlayerMissileSpeed: CGFloat = 300

这是我们指定的让导弹在 1 秒内必须移动的距离。现在，将最后添加的那段代码修改为：

// calculate distance
let distance = sqrt(pow(destination.x - playerSprite.position.x, 2) +
  pow(destination.y - playerSprite.position.y, 2))

// run the sequence of actions for the firing
let duration = NSTimeInterval(distance / PlayerMissileSpeed)
let missileMoveAction = SKAction.moveTo(destination, duration: duration)
playerMissileSprite.runAction(missileMoveAction) {
  self.playerMissileSprite.hidden = true
}

这回，我们将硬编码的动画时长替换成牛顿位移公式计算出来的距离除以速度。运行程序，你将发行导弹的飞行速度是固定的，无论终点位于何方。

接下来是创建一个 moveTo() 动作。虽然有点麻烦，但你一旦创建了动作之后就不用操心了，因为 Sprite Kit 会自动为你完成剩下的动画工作。

命中目标

现在，导弹完全就无视于炮台的存在——飞船除了发出一束绿光之外什么也不做！

让我们来解决它。之前，我们使用了一种简单的基于碰撞半径的检测方法。我们也增加了一个 PlayerMissileRadius 常量，因此我们可以用同样的方法来检测导弹和炮台之间的碰撞，正如飞船和炮台之间的碰撞一样。

新增一个方法：

func checkMissileCannonCollision() {

  if !playerMissileSprite.hidden {

    let deltaX = playerMissileSprite.position.x - turretSprite.position.x
    let deltaY = playerMissileSprite.position.y - turretSprite.position.y

    let distance = sqrt(deltaX * deltaX + deltaY * deltaY)
    if distance <= CannonCollisionRadius + PlayerMissileRadius {

      playerMissileSprite.hidden = true
      playerMissileSprite.removeAllActions()

      cannonHP = max(0, cannonHP - 10)
      updateHealthBar(cannonHealthBar, withHealthPoints: cannonHP)
    }
  }
}

这个方法就像 checkShipCannoCollision() 方法一样，首先计算二个精灵之间的距离，当距离小于二者碰撞半径之和时，则可认为碰撞有效。

如果碰撞有效，首先隐藏导弹，取消它的动画；然后扣减炮台的生命点，重新绘制它的血槽。简单！

在 update() 方法中，调用 checkMissileCannonCollisoin() 方法：

checkMissileCannonCollision()

运行程序，你会发现你可以对敌人造成伤害了！

这里，最好给导弹一些音效。就像在之前的飞船-炮台碰撞中所做的一样，我们可以使用 Sprite Kit 动作来播放声音。在 GameScene 中增加两个属性：

var missileShootSound: SKAction!
var missileHitSound: SKAction!

在 didMoveToView() 方法中初始化它们：

missileShootSound = SKAction.playSoundFileNamed("Shoot.wav", waitForCompletion: false)
missileHitSound = SKAction.playSoundFileNamed("Hit.wav", waitForCompletion: false)

在 touchesEnded() 方法中，将 playerMissileSprite.runAction(missileMoveAction) 一行替换为：

playerMissileSprite.runAction(SKAction.sequence([missileShootSound, missileMoveAction])) {

与之前执行单个的 move 动作不同，我们创建了一个序列用于在移动导弹的同时播放声音。

最终，在 checkMissileCannonCollision() 方法中，在内层 if 语句内的最后加入：

runAction(missileHitSound)

这就是我们所做的：导弹发射时播放“嗖嗖”的音效，如果你瞄得准——并且打到了炮塔，则播放“嘣”的爆炸声。

挑战

这里，我们给你留了一个作业：你能够让炮台向飞船还击吗？

你已经学习了每一个有用的知识点，为了加深理解，最好来一场真枪实弹的练习。在你尽最大努力之前，请不要翻看答案！

参考答案：让炮台进行还击

你所需要做的就是创建一个新的炮弹精灵（使用 CannonMissile.png 图片），计算距离，然后发送炮弹。你已经知道发射角度了，因为炮塔指向的方向就是玩家。moveTo() 动作的终点就是当前的玩家位置。

碰撞检测和之前的方法一样：当炮弹和玩家之间的距离小于二者的碰撞半径之和，则认为炮弹打中了玩家。为了让游戏有一定的难度，炮台能够一次发射多枚炮弹（提示：应该用数组来保存炮弹精灵！）。

完成了吗？觉得自己干的还不错吧？接下来还有一个挑战！

当前，当前炮弹是以直线飞行。但如果炮弹是热辐射自导引的呢？热辐射自导引的炮弹会根据玩家的位置自动调整飞行路线。

你已经学会了使用三角学来解决问题，那么到底该怎么做呢？提示：与之前只计算一次炮弹的速度和方向不同，我们应该在每一帧都计算它们，就像飞船的飞行一样。

参考答案：能够热辐射自导引的炮弹

因为需要在每一帧都计算炮弹的速度和飞行方向，我们不能再使用 moveTo() 动作。我们必须自定义动画。不断地根据玩家位置来调整炮弹的速度。要了解更多关于“追寻”的行为，请参考游戏 AI 教程。

为自导引炮弹加上点时间限制，如果玩家躲避的时间足够长就能躲开这个炮弹，否则游戏就太难玩了。

完成得怎么样？你的飞船是像汤姆.克鲁斯一样在躲避炮弹，还是已经安然逃脱了？

加上轨道防御盾

为了让我们的游戏更有挑战性，我们将给敌人一个防御盾。这个防御盾是一个小行星，围绕着炮台旋转并抵御住一切试图靠近它的导弹。

在 GameScene.swift 头部新增如下常量：

let OrbiterSpeed: CGFloat = 120
let OrbiterRadius: CGFloat = 60
let OrbiterCollisionRadius: CGFloat = 20

在 GameScene 中增加几个属性：

let orbiterSprite = SKSpriteNode(imageNamed:"Asteroid")
var orbiterAngle: CGFloat = 0

在 didMoveToView() 方法中，初始化新角色：

addChild(orbiterSprite)

然后，在 GameScene 中加入以下方法：

func updateOrbiter(dt: CFTimeInterval) {

  // 1
  orbiterAngle = (orbiterAngle + OrbiterSpeed * CGFloat(dt)) % 360

  // 2
  let x = cos(orbiterAngle * DegreesToRadians) * OrbiterRadius
  let y = sin(orbiterAngle * DegreesToRadians) * OrbiterRadius

  // 3
  orbiterSprite.position = CGPointMake(cannonSprite.position.x + x, cannonSprite.position.y + y)
}

防御盾会围绕炮台旋转。也就是说，它作圆形轨道运动，一圈接一圈，周而复始。要做到这个，你需要两点：半径——它是防御盾距离炮台中心的距离，角度——它是防御盾沿圆心所旋转的距离。

在 updateOrbiter() 方法中，我们做了这些事情：

1. 根据某个速度（OrbiterSpeed 常量）和时间差（delta time）增加旋转角度，这个角度经过 % 360 取余后得到一个 0-360° 之间的角度——这其实不是很必要，因为哪怕是角度在这个范围外 cos 和 sin 函数也不会有什么问题，只不过如果角度太大，浮点数的精度可能会成为一个问题（而且在测试时，如果角度限制在这个范围内，对我们来说更直观一些）。

2. 用 sin() 和 cos() 计算防御盾的 x 和 y。这需要用到半径（三角形的斜边）和当前角度，而返回的是另外两边（邻边和对边）。后面会细述。

3. 设置防御盾的新位置，用炮台的中心位置加上 x 和 y。

注意：% 运算符用于将 orbiterAngle 限制在 0-360°，虽然 orbiterAngle 实际上是一个浮点数。在 C/O-C 中，你必须用 fmod() 函数，因为 % 运算符只能用于整数，但 Swift 中 % 运算符支持浮点数！

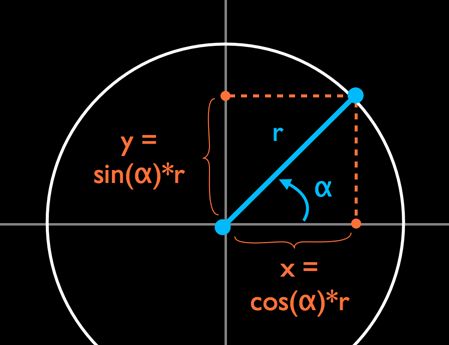
你曾经看到过 sin() 和 cos() 的用法，但可能还不清楚它们是怎样实现的。我们知道这两个函数可以用来在已知一个角和斜边的情况下，计算出直角三角形的另外两边。

但你难道不奇怪这是为什么吗？

让我们来画一个圆：

上图描述了防御盾围绕炮台旋转的情况。圆表示防御盾的路径，圆心位于炮台的中央。

开始时防御盾的角度为 0,这个角度随着时间增加直到它又回到起点。如上图所示，圆的半径表示防御盾到圆心的距离。

因此，在给定角度和半径的情况下，你可以用 cos 和 sin 获得位置的 x 和 y：

现在来看一下正弦波和与余弦波：

x 轴是圆的角度，从 0° 到 360°（或者 0 到 2π 个弧度）。y 轴是 -1 到 +1，如果你的半径不是 1，则 y 轴的取值范围是 -radius 到 +radius。

因为角度是从 0-360 增加，在正弦波和余弦波的 x 轴上找到这个角度，则可以从 y 轴上查到这个角度的 x 值和 y 值：

1. 如果角度为 0, cos(0) 是 1 * radius，sin(0)是 0 * radius。转换到圆的 x,y 坐标上就是：x 等于半径，但 y 等于 0。

2. 如果角度为 45°，cos(45) 和 sin(45) 都是 0.707 * radius，也就是说是位于圆上 x=y 的位置。（注意：如果你使用计算器进行计算，请先把 DEG 模式打开。如果你得到的数字不是这个，则说明是 RAD 模式）。

3. 如果角度是 90°，cos(90) 是 0 * radius，sin(90) 是 1 * radius。则当前位置应该位于圆的正上方，x,y 坐标应当为 （0,radius）。

4. 依次类推。要更彻底地了解圆上的坐标与 sin、cos 甚至是 tan 函数的关系，请看这里。

尝出点味道了吗？好。发现 sine 曲线和 cos 曲线其实非常像了吗？事实上，余弦波只是在正弦波的基础上偏移 90°。去告诉你的朋友和家人，你所知道的关于正弦和余弦的数学吧！

回到代码中来。在 update() 方法中的最后调用 updateOrbiter() 方法：

updateOrbiter(deltaTime)

运行程序。你将看到炮台外面有一个旋转着的轨道防御盾！

我们还以让防御盾成自转运动：将下列代码加在 updateOrbiter() 最后：

orbiterSprite.zRotation = orbiterAngle * DegreesToRadians

通过设置 orbiterAngle，防御盾自转的方向和它相对于炮台旋转的角度一致了，就像月亮总是用同一面对着地球。尽管看起来它根本就没有在自转，但实际上却是自转的！

如果你加入一个负号，比如 orbiterSprite.zRotation = -orbiterAngle*DegreesToRadians，则防御盾将相对于炮台做相反方向的自转，而不是总是面对着它。随便你使用哪种效果。运行程序，测试一小会。

让我们给繁育吨增加一个任务。如果导弹靠得太近，防御盾将摧毁导弹使其无法对炮台造成伤害。增加下列方法：

func checkMissileOrbiterCollision() {

  if !playerMissileSprite.hidden {

    let deltaX = playerMissileSprite.position.x - orbiterSprite.position.x
    let deltaY = playerMissileSprite.position.y - orbiterSprite.position.y

    let distance = sqrt(deltaX * deltaX + deltaY * deltaY)
    if distance < OrbiterCollisionRadius + PlayerMissileRadius {

      playerMissileSprite.hidden = true
      playerMissileSprite.removeAllActions()

      orbiterSprite.setScale(2)
      orbiterSprite.runAction(SKAction.scaleTo(1, duration: 0.5))
    }
  }
}

同时，别忘了在 update() 方法最后调用它：

checkMissileOrbiterCollision()

这段代码看起来太熟悉了，基本上跟 checkMissileCannonCollision() 没什么两样。当碰撞有效，导弹精灵会被移除。只不过这一次，我们不播放声效，而是添加一个放大效果，将防御盾大小增加到两倍，然后又让它恢复原样。看起来就像防御盾“吞噬掉”了导弹一样！

运行程序，查看防御盾的效果。

在游戏结束画面中使用三角学

我们还可以用 sin 和 cos 做更多的事情。它们不仅仅只能用于三角形计算和创建圆型路径——它们还能用于动画的处理。

用于展示动画效果的好时机是游戏结束画面。在 GameScene.swift 顶部增加如下常量：

let DarkenOpacity: CGFloat = 0.8

在 GameScene 类中加入以下属性：

var darkenLayer: SKSpriteNode?
var gameOverLabel: SKLabelNode?
var gameOver = false
var gameOverElapsed: CFTimeInterval = 0

我们会用这些属性来记录游戏状态和显示“Game Over”信息。

然后，添加如下方法：

func checkGameOver(dt: CFTimeInterval) {

  // 1
  if playerHP > 0 && cannonHP > 0 {
    return
  }

  if !gameOver {

    // 2
    gameOver = true
    gameOverElapsed = 0
    stopMonitoringAcceleration()

    // 3
    let fillColor = UIColor(red: 0, green: 0, blue: 0, alpha: 1)
    darkenLayer = SKSpriteNode(color: fillColor, size: size)
    darkenLayer?.alpha = 0
    darkenLayer/.position = CGPoint(x: size.width/2, y: size.height/2)
    addChild(darkenLayer!)

    // 4
    let text = (playerHP == 0) ? "GAME OVER" : "Victory!"
    gameOverLabel = SKLabelNode(fontNamed: "Helvetica")
    gameOverLabel?.text = text
    gameOverLabel?.fontSize = 24
    gameOverLabel?.position = CGPoint(x: size.width/2 + 0.5, y: size.height/2 + 50)
    addChild(gameOverLabel!)

  } else {

    // 5
    darkenLayer?.alpha = min(DarkenOpacity, darkenLayer!.alpha + CGFloat(dt))
  }
}

这个方法用于判断游戏是否结束，如果判断为 true，进行游戏结束动画：

1. 如果玩家或者炮台的血值为 0，游戏结束。

2. 如果游戏结束，设置 gameOver 为 true，关闭加速计。

3. 创建一个新的，纯黑色的颜色层，将它添加到所有对象的前面。它的 alpha 一开始设置为 0，这样它就完全透明。在后面的代码中，我们会对这个透明度进行动画，使其呈现渐入的效果。

4. 加一个新的文字标签到屏幕中央。如果玩家获胜，文字内容为“Victory!”，否则为“Game Over”，胜负根据玩家的血值来判定。

5. 上面的代码只会创建一次游戏结束画面——在此之后，代码将进入 else 分支。在这里，我们对颜色图层的 alpha 值进行动画，由 0 渐变到 0.8（即 DarkenOpacity 常量）——接近于完全不透明，但又不是。

在 update() 底部调用 checkGameOver() :

checkGameOver(deltaTime)

在 touchesEnded() 顶部加入以下代码：

if gameOver {
  let scene = GameScene(size: size)
  let reveal = SKTransition.flipHorizontalWithDuration(1)
  view?.presentScene(scene, transition: reveal)
  return
}

这段代码在用户点击游戏结束画面后重新启动游戏。

运行程序。向炮台开火或者撞击，一直到你们中的某一个血掉光。屏幕会渐渐暗下来，游戏结束字样显示。游戏不在对加速计产生响应，只不过动画仍然还会继续：

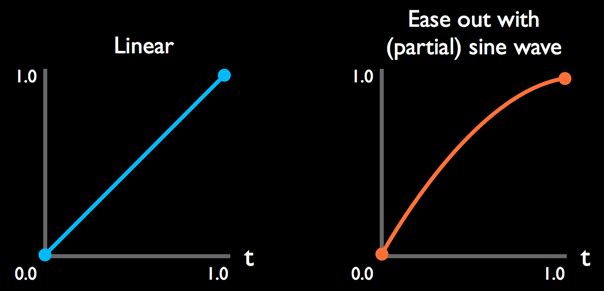
一切顺利，但说好的 sin 和 cos 呢？如你所见，黑色图层的渐变动画是以线性方式进行的。也就是说透明度由高到低是以固定的速度变化的。

我们可以改进这一点——通过 sin() 函数来调整渐变时间。这叫做“淡入淡出”，我们将使用的是“淡出”。

注意：你也可以用 runAction() 方法让 alpha 渐变，因为它支持各种淡入淡出模式。但是，出于教学的目的，我们要在这里教大家学习淡入淡出背后的数学只是，而不是教大家怎样使用 Sprite Kit。

在 GameScene.swift 顶部加入一个新常量：

let DarkenDuration: CFTimeInterval = 2

然后，将 checkGameOver() 方法中 else 分支中的代码修改为：

gameOverElapsed += dt
if gameOverElapsed < DarkenDuration {
  var t = CGFloat(gameOverElapsed / DarkenDuration)
  t = sin(t * Pi / 2) // ease out
  darkenLayer.alpha = DarkenOpacity * t
}

gameOverElapsed 负责记录游戏结束后所经过的时间。黑色图层(DarkenDuration)的渐入需要耗时 2 秒。变量 t 用于计算整个过程过去了多少。无论 DarkenDuration 值是多少，这个值都会在 0-1.0 之间。

然后是最关键的地方：

t = sin(t * Pi / 2) // ease out

这会将线性插值进行某种转换，如下图所示：

运行程序，查看“淡出”效果。如果你无法看到有任何不同，则可以将“ease out”一行注释，或者改变动画时长。效果很微妙，但确实存在。

注意：如果你想快速看到效果，将 cannonHP 调整为 10，这样你只需要击中一次就能让游戏结束。

淡入淡出是一种细微的效果，我们可以用弹性效果来使其更加明显——因为能够反弹的东西更加有趣！

在 checkGameOver() 方法的 else 分支内，刚刚加入的代码之后，加入：

// label position
let y = abs(cos(CGFloat(gameOverElapsed) * 3)) * 50
gameOverLabel.position = CGPoint(x: gameOverLabel.position.x, y: size.height/2 + y)

这是什么意思？还记的余弦波的样子吗：

如果你对 cos() 进行取绝对值——用 abs() 函数——则小于 0 的部分将被翻转。这个曲线看起来就像是反弹，不是吗？

因为这些函数的值分布在 0.0 到 1.0 之间，乘以 50 之后就会让值放大到 0-50 之间。cos() 的参数通常是一个角度，但我们传递了一个 gameOverElapsed 时间进去，导致 cos 根据时间曲线来移动。

系数 3 的使用使它变化得更快。你可以调整这些值直到你认为 OK。

运行程序，查看文字的弹簧效果：

你使用了余弦波的形状来描述文字标签的弹簧运动。余弦非常适合于描述各种事情！

最后一件事情是让弹簧运行随时间曲线逐渐减少振幅。这需要增加一个衰减系数。在 GameScene 中添加一个属性：

var gameOverDampen: CGFloat = 0

当游戏结束，我们需要将这个值重置为 1.0 以便进行有效衰减。当文字做弹簧运动时，衰减系数又会逐渐递减到 0.

在 checkGameOver() 方法中，找到我们设置 gameOver 为 true 的 if 语句块，在设置完 gameOver 之后添加这句：

gameOverDampen = 1

在 else 块中，将 “// label positon” 一句注释后面的代码修改为：

let y = abs(cos(CGFloat(gameOverElapsed) * 3)) * 50 * gameOverDampen
gameOverDampen = max(0, gameOverDampen - 0.3 * CGFloat(dt))
gameOverLabel.position = CGPoint(x: gameOverLabel.position.x, y: size.height/2 + y)

这和前面几乎没什么区别，除了将 y 乘以衰减系数并逐步将衰减系数从 1.0 递减到 0 以外（永远不要小于 0；也就是要用 max() 来进行限制）。运行程序，进行测试！

接下来做什么？

这是“游戏编程中的三角学”系列教程的完整示例代码。

恭喜你，你已经深入学习了 sin、cos 和 tan 函数，也见到了如何在真实游戏中使用它们的例子。我希望你能够明白，三角形在游戏中是何等的有用！

注意，我们并没有太多涉及 arcsin 和 arccos。比起 arctan 来说它们很少见，最常见的例子是用 arccos 计算两个任意向量之间的夹角——例如，模拟光束照射到镜面上的反射，或者根据对象与光源之间的角度计算这个对象的亮度。

你可以在Tiny Wings tutorial中找到更多关于三角函数的非常有用的例子。它使用 cos 函数在游戏中绘制极其优美的山脉曲线。

如果想在更多游戏开发中使用你刚学到的技巧，但不知道从何开始，请阅读我们的iOS 游戏开发教程。它将启动你的游戏开发之旅！请访问我们的论坛，分享你在使用三教数学中的苦与乐。合理地使用你的新技能！

声明：游戏中使用的图片来自于 Kenney Vleugels，声音来自于 freesound.org。