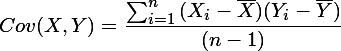文本挖掘之降维之特征抽取之主成分分析（PCA）

PCA（主成分分析）

作用：

1、减少变量的的个数

2、降低变量之间的相关性，从而降低多重共线性。

3、新合成的变量更好的解释多个变量组合之后的意义

PCA的原理：

样本X和样本Y的协方差(Covariance)：

协方差为正时说明X和Y是正相关关系，协方差为负时X和Y是负相关关系，协方差为0时X和Y相互独立。

Cov(X,X)就是X的方差(Variance).

当样本是n维数据时，它们的协方差实际上是协方差矩阵（对称方阵），方阵的边长是。比如对于3维数据(x,y,z)，计算它的协方差就是：

若，则称是A的特征值，X是对应的特征向量。实际上可以这样理解：矩阵A作用在它的特征向量X上，仅仅使得X的长度发生了变化，缩放比例就是相应的特征值。

当A是n阶可逆矩阵时，A与P^-1Ap相似，相似矩阵具有相同的特征值。

特别地，当A是对称矩阵时，A的奇异值等于A的特征值，存在正交矩阵Q（Q^-1=Q^T），使得：

对A进行奇异值分解就能求出所有特征值和Q矩阵。

     D是由特征值组成的对角矩阵

由特征值和特征向量的定义知，Q的列向量就是A的特征向量。

实现步骤：

首先我们有N个P维的向量要区分，X1,X2...Xn。P比较大，则处理所有向量的数据量较大，我们将其降至d维（d<P）。首先构造矩阵S=[X1,X2...Xn],算出协方差矩阵C（P维方阵），求出C的特征值T和特征向量V。将特征值按从大到小排列取出前d个特征值，并将这些特征值对应的特征向量构成一个投影矩阵L。使用S*L则得到降维后的提出主成分的矩阵。下面附上自己做的小实验。

  X1 = [1,2,4]   X2 = [10,4,5]  X3 = [100,8,4]

  根据经验上述3维向量中，第一维和第二维是区分的要素且第一维比第二维区分度更大。于是我们构造矩阵S,

 1） S = [1,2,4;10,4,5;100,8,5]

  2）计算出S的协方差矩阵C = COV(S),

  C =

  1.0e+003 *

    2.9970    0.1620    0.0180
    0.1620    0.0093    0.0013
    0.0180    0.0013    0.0003

  求出协方差矩阵C的特征值T和特征向量V，[T,V] = eig(C)

 V =

   -0.0235    0.0489   -0.9985
    0.5299   -0.8464   -0.0540
   -0.8478   -0.5303   -0.0060

  T=

  1.0e+003 *

   -0.0000         0         0
         0    0.0008         0
         0         0    3.0059

  取出第3个和第2个特征值以及相对应的特征向量构成投影矩阵L（实际上可以只取第三维）

  L =

   -0.9985    0.0489
   -0.0540   -0.8464
   -0.0060   -0.5303

  使用S*L则得到新的降维后的矩阵N

  N =

   -1.1305     -3.7651
  -10.2310    -5.5481
  -100.3120   -4.5327

  则提取出了可以用于区分的二维。