选择排序:堆排序
堆排序(Heap Sort):使用堆这种数据结构来实现排序。
先看下堆的定义:
最小堆(Min-Heap)是关键码序列{k0,k1,…,kn-1},它具有如下特性:
ki<=k2i+1,
ki<=k2i+2(i=0,1,…)
简单讲:孩子的关键码值大于双亲的。
同理可得,最大堆(Max-Heap)的定义:
ki>=k2i+1,
ki>=k2i+2(i=0,1,…)
同样的:对于最大堆,双亲的关键码值大于两个孩子的(如果有孩子)。
堆的特点:
- 堆是一种树形结构,而且是一种特殊的完全二叉树。
- 其特殊性表现在:它是局部有序的,其有序性只体现在双亲节点和孩子节点的关系上(树的每一层的大小关系也是可以体现的)。兄弟节点无必然联系。
- 最小堆也被称为小顶堆(根节点是最小的),最大堆也被称为大顶堆(根节点是最大的)。我们常利用最小堆实现从小到大的排序,最大堆实现从大到小的排序。
要想实现排序,第一个问题:如何建堆?(以最小堆为例,最大堆同理)
建堆:从最后一个内部节点开始,不断地向下调整,直到根节点。
画个流程图,看得更明白:矩形框表示要调整的位置
仔细看上面的流程图,相信你一定可以清楚明白整个调整过程。
建堆代码:我们使用顺序结构存储堆(可不要以为树形结构一定得使用链表来实现),向下调整(heapSiftDown())的方法是关键,建堆的代码如下:
void heapSiftDown(int a[], int n, int pos) //从pos位置向下调整
{
int i = pos;
int j = 2 * i + 1; //j为i的左孩子
while (j < n)
{
if (j + 1 < n && a[j + 1]<a[j]) //如果右孩子存在,并且右孩子<左孩子
j++;
if(a[i] < a[j]) //已满足堆序,不需调整
break; //为什么不是continue?因为子树已经排好堆序,结合流程图想想?
swap(a[i], a[j]); //交换元素
i = j;
j = 2 * i + 1;
}
}
void createHeap(int a[], int n) //建堆
{
if (a && n > 1)
{
for (int i = (n - 2) / 2; i >= 0; i--) //(n-2)/2是最后一个内部节点的下标
heapSiftDown(a, n, i);
}
}
建堆时间复杂度:
建堆的时间复杂度是O(n),推导比较复杂。下面粘贴出从资料上找到的推导过程:
对于n个节点的堆,其对应的完全二叉树的层数是logn。若i为层数,则第i层上的节点数最多为2^i(i>=0)。建堆时,每个非叶子节点都调用了一次heapSiftDown()函数,并且每个节点最多调整到最底层,即第i层上的节点调整到最底层的调整次数为logn-i(最大的),则建堆的时间复杂度为
以上复杂度分析参考张铭等《数据结构与算法》,推导过程其实并不重要,关键在于我们可以肯定的是建堆是很快的,最多是线性的。
建好堆之后,如何实现堆排序呢?排序之前,我们先看有关堆的两个操作:插入和删除。理解了这两个操作,排序就自然清楚了。堆的插入:插入时总是把新节点插入到堆的最后,并从插入位置向上调整,直到根节点或在此之前已满足堆序。
举个例子解释下这个过程:红色的3是新添的节点。
注意:向上调整的时候,只关注插入位置到根节点的路径,其它路径上的节点是不用调整的。理由很简单:它们已是堆序。这一点可要想清楚了!
向上调整的代码如下:
const int MAX=20;
void heapSiftUp(int a[], int n) //向上调整
{
int i,j;
j = n-1;
i = (i-1)/2; //i为j的父节点
while(i>=0)
{
if(a[j] >= a[i])
break;
swap(a[i], a[j]);
j = i;
i = (j-1)/2; //更精确的写法: i=j%2?(j-1)/2:(j-2)/2;
}
}
void addToHeap(int a[], int n, int data)
{
/*
前提:数组a已排好堆序且数组还有多余位置存放新节点
*/
if(n+1>MAX)
{
printf("数组已满!无法插入\n");
return;
}
n++;
a[n-1]=data; //把新节点加到最后
heapSiftUp(a, n);
}
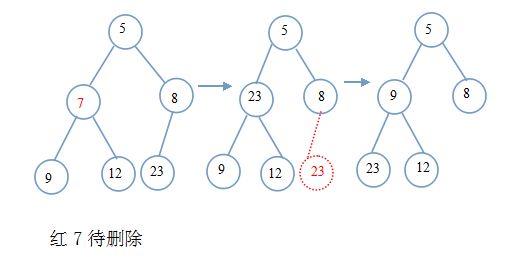
堆的删除:删除操作总是在堆顶进行(也有的说,可以在任意位置删除,但做法一样),我们把最后一个节点填入待删除位置。然后从该位置向下调整。
同样给个示例图:结合上面以给出的向下调整代码,则很好得到堆删除的代码,为了通用性,我们给出指定位置删除的代码:
void deleteAt(int a[], int &n, int pos) //删除pos位置的节点
{
if(pos >= n)
{
printf("删除的位置不对!\n");
return;
}
a[pos] = a[n-1]; //把最后一个节点填到待删除位置
n--;
heapSiftDown(a, n, pos); //向下调整
}
特别地,删除堆顶就是 deleteAt(a, n, 0);
有了上面的铺垫,堆排序就呼之欲出了。堆排序步骤:
- 先建好堆。
- 不断地删除堆顶即可(删除前记得打印堆顶元素),直到只剩下一个元素。
#include<iostream>
#include<ctime>
using namespace std;
void heapSiftDown(int a[], int n, int pos) //从pos位置向下调整
{
int i = pos;
int j = 2 * i + 1; //j为i的左孩子
while (j<n)
{
if (j + 1 < n && a[j + 1]<a[j]) //如果右孩子存在,并且右孩子<左孩子
j++;
if (a[i] < a[j]) //已满足堆序,不需调整
break; //为什么不是continue?因为子树已经排好堆序
swap(a[i], a[j]); //交换元素
i = j;
j = 2 * i + 1;
}
}
void createHeap(int a[], int n) //建堆
{
if (a && n > 1)
{
for (int i = (n - 2) / 2; i >= 0; i--)
heapSiftDown(a, n, i);
}
}
void deleteAt(int a[], int &n, int pos) //删除pos位置的节点
{
if (pos >= n)
{
printf("删除的位置不对!\n");
return;
}
a[pos] = a[n - 1]; //把最后一个节点填到待删除位置
n--;
heapSiftDown(a, n, pos); //向下调整
}
void HeapSort(int a[], int n) //堆排序
{
if (a && n > 1)
{
createHeap(a, n);
while (n > 1)
{
printf("%4d", a[0]);
deleteAt(a, n, 0);
}
printf("%4d\n", a[0]);
}
}
int main()
{
printf("******堆排序演练***by David***\n");
printf("原序列\n");
const int N = 12;
int *a = new int[N];
srand((unsigned)time(NULL));
for (int i = 0; i < N; i++)
{
a[i] = rand() % 100;
printf("%4d", a[i]);
}
printf("\n");
printf("经过堆排序\n");
HeapSort(a, N);
delete[]a;
system("pause");
return 0;
}
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void Swap(int& a, int& b)
{
if(a!=b)
{
a ^= b;
b ^= a;
a ^= b;
}
}
//维护最大堆(从指定位置pos,向下调整)
void MaxHeapify(int a[], int n, int pos)
{
int i, j;
i = pos;
j = 2 * i + 1; //节点i的左孩子
while (j < n)
{
if (j + 1 < n && a[j] < a[j + 1])
j++;
if (a[i] < a[j])
Swap(a[i], a[j]);
i = j;
j = 2 * i + 1;
}
}
//构建最大堆
void BuildMaxHeap(int a[], int n)
{
if (a && n > 1)
{
int i, j;
i = (n - 2) >> 1;
while (i >= 0)
{
MaxHeapify(a, n, i);
i--;
}
}
}
//堆排序
void HeapSort(int a[], int n)
{
if (a && n > 1)
{
//先建堆
BuildMaxHeap(a, n);
while (n > 1)
{
//交换首尾元素
Swap(a[0], a[n - 1]);
//堆规模减一
n--;
//再次从堆顶调增
MaxHeapify(a, n, 0);
}
}
}
int main()
{
printf("******最大堆实现从小到大排序***by David***\n");
srand((unsigned)time(0));
int a[12];
printf("原序列\n");
for (int i = 0; i < 12; i++)
{
a[i] = rand() % 100;
printf("%4d", a[i]);
}
printf("\n经过堆排序\n");
HeapSort(a, 12);
for (int i = 0; i < 12; i++)
printf("%4d",a[i]);
printf("\n");
system("pause");
return 0;
}

专栏目录看这里:
- 数据结构与算法目录
- c指针