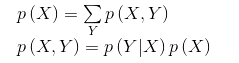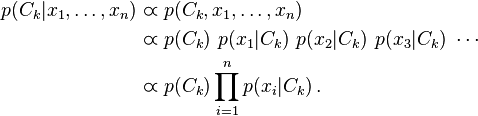概率图模型基础
一、概念引入
很多事情是具有不确定性的。人们往往希望从不确定的东西里尽可能多的得到确定的知识、信息。为了达到这一目的,人们创建了概率理论来描述事物的不确定性。在这一基础上,人们希望能够通过已经知道的知识来推测出未知的事情,无论是现在、过去、还是将来。在这一过程中,模型往往是必须的,什么样的模型才是相对正确的?这又是我们需要解决的问题。这些问题出现在很多领域,包括模式识别、差错控制编码等。
概率图模型是解决这些问题的工具之一。从名字上可以看出,这是一种或是一类模型,同时运用了概率和图这两种数学工具来建立的模型。那么,很自然的有下一个问题。
二、为什么要引入概率图模型
对于一般的统计推断问题,概率模型能够很好的解决,那么引入概率图模型又能带来什么好处呢?
LDPC码的译码算法中的置信传播算法的提出早于因子图,这在一定程度上说明概率图模型不是一个从不能解决问题到解决问题的突破,而是采用概率图模型能够更好的解决问题。
《模式识别和机器学习》这本书在图模型的开篇就阐明了在概率模型中运用图这一工具带来的一些好的性质,包括
1. They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models.
2. Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph.
3. Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.
简而言之,就是图使得概率模型可视化了,这样就使得一些变量之间的关系能够很容易的从图中观测出来;同时有一些概率上的复杂的计算可以理解为图上的信息传递,这是我们就无需关注太多的复杂表达式了。最后一点是,图模型能够用来设计新的模型。所以多引入一数学工具是可以带来很多便利的,我想这就是数学的作用吧。
当然,我们也可以从另一个角度考虑其合理性。我们的目的是从获取到的量中得到我们要的信息,模型是相互之间约束关系的表示,而数据的处理过程中运用到了概率理论。而图恰恰将这两者之间联系起来了,起到了一个很好的表示作用。
三、加法准则和乘法准则
涉及到概率的相关问题,无论有多复杂,大抵都是基于以下两个式子的——加法准则和乘法准则。
第一个式子告诉我们当知道多个变量的概率分布时如何计算单个变量的概率分布,而第二个式子说明了两个变量之间概率的关系。譬如X,Y之间相互独立时应有
还有一个是著名的贝叶斯公式,这和上面的乘法准则是一样的(当然分母也可以用加法公式写,这样就是那个全概率公式了)
四、图和概率图模型
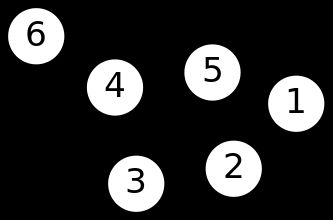
下面这张图片描述的就是图,它是由一些带有数字的圆圈和线段构成的,其中数字只是一种标识。我们将圆圈称为节点,将连接圆圈的节点称为边,那么图可以表示为G(V,E)。
如果边有方向,称图为有向图,否则为无向图;
两个节点是连通的是指两节点之间有一条路;
路是由节点和边交叉构成的;
上述定义都不太严格,具体可参考图论相关知识。
有向图模型(贝叶斯网络)
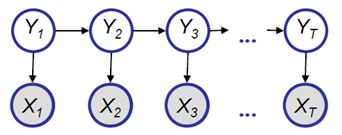
举个例子,譬如有一组变量X1,X2….XN,如果每个变量只与其前一个变量有关(1阶马尔可夫过程),那么以下等式成立
那么如何用图来表示这一关系呢?自然,我们要表示的是右边的式子,右边的式子表示了变量之间的联系。而当我们观察条件概率时,我们发现我们必须要指明哪个是条件。如果我们采用变量为节点,采用无向图这种节点等价的关系显然不能直接描述条件概率,因此这里选择了有向图来描述这一关系,即表示为P(X2|X1)
那么此时上述的1阶马尔可夫过程表示为,注意其中没有箭头指向X1,故表示p(X1)意味着无条件。
有向图模型,或称贝叶斯网络,描述的是条件概率,或许这就是其被称为贝叶斯网络的原因吧。此处不再细说。
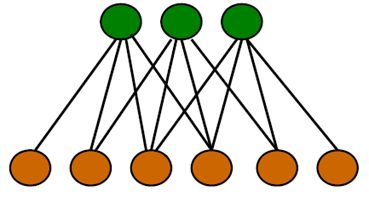
无向图模型(马尔可夫随机场)
构造有向图模型需要变量之间显式的、很强的约束关系。即首先要有条件概率分布关系,其次还要是可求的。为了达到这一目的,很有可能我们要做很多不切实际的假设。譬如朴素贝叶斯(Naive Bayes)的假设就相当的Naive。如下所示,其假设往往是不成立的。
那什么是更弱的假设呢?很多时候我们知道两个变量之间一定是相关的,但我们不知道到底是怎么相关的。这时候我们也可以用其相关性来构造概率图模型。相关是不分方向的,此时我们应该选择无向图来表示。
和相关对应的是独立(实际上是不相关,这里不做区分了),我们可以这样来构造图模型,如果两个节点之间独立,那么没有路使其相连。条件独立即去掉条件中节点后,两节点之间没有路相连。具体可由《PATTERN RECOGNITION and MACHINE LEARNING》中的例子阐述
因子图
按理来说,无向+有向就全了。为什么还有一类呢?或许严格来说不应该将因子图和上述两类并列的,但我不知道放到哪里去……
因子,从名字中就强调了的两个字一定是其重要组成部分。而上述的两类图表现出的变量之间最终的关系实际上就是将概率分布化为了多个式子的乘积。对于多项式而言,我们有因式分解。譬如在解高次方程的时候,我们非常希望方程能够分解为多个低次方程的乘积。那么,对于概率分布函数而言,我们也希望能够这样做,即
![]()
其中,![]() 是
是![]() 中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
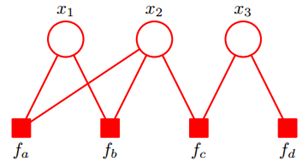
那么这一个式子的因子图表示如下
这个例子,我们总结一下因子图是什么。因子图有两类节点,一是变量节点,另一类为因子节点。这两类节点的内部没有边直接相连,变量的概率分布可以因式分解为因子节点的函数的乘积,因子节点的函数变量包括与其直接相连的变量节点。
三类图各有特点,适用于不同的场合,且这三类图是可以相互转换的。转换方式此处不做描述。
五、举例分析
HMM,隐马尔可夫模型,是一种有向图模型。这和上述的1阶马尔可夫过程是类似的,不同之处在于我们能够观测到的量不是过程本身,而是与其有一定关系的另一些量。HMM应用很广泛,可以参考隐马尔可夫模型(HMM)攻略 。
RBM,限制玻尔兹曼机,无向图模型。了解深度学习相关知识的对这个应该很熟悉,看到无向图模型的时候就会发现,都有一个势能函数。这个我不太会,就不介绍了。
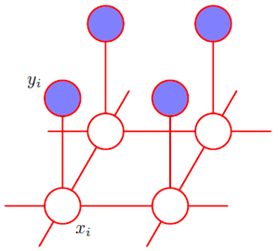
图像去噪,PRML中的一个例子,无向图模型。目的是从观测到的有噪声的图片中恢复出原始图片,做出的假设是观察到的图片像素点和原始图片相关,同时原始图片相邻像素点之间相关。
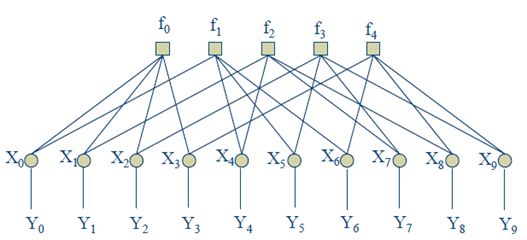
LDPC译码,差错控制编码中的例子,因子图。其中Y是观测节点,和变量节点X相关,同时f是因子节点,约束是连接该节点的变量节点模2和为0。(也可以去掉Y,这样就是比较标准的因子图了)
六、推理:和积算法
本节将以和积算法为例,说明概率图模型下的概率计算过程。和积算法也用在LDPC译码过程中,这一过程也将证实“一些概率上的复杂的计算可以理解为图上的信息传递,这是我们就无需关注太多的复杂表达式了”这一观点。和积算法作用在因子图上,旨在计算边缘概率![]()
其中,表示除![]() 之外的变量集合。 具体算法推导过程可以参考PRML的p402。这里仅简单叙述。
之外的变量集合。 具体算法推导过程可以参考PRML的p402。这里仅简单叙述。
最简单的情况是只有一个变量节点和因子节点,这个时候就不用算了。但实际情况不可能是这样的,但这并不影响我们采用化繁为简的思路。
这里我们做出一个假设是一旦我们断开了一条变量节点和因子节点的边,那么因子图就变成了两个互不连通的因子图。(否则则有环,但实际上很多有环的图采用这一算法也得到了很好的结果)
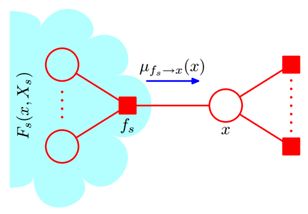
考虑图上的信息流动,从因子节点fs到变量节点x以及从变量节点x到因子节点fs。充分利用上述假设带来的结果,最后我们可以推得
此处不做具体解释,仅说明何为“图上的信息传递”。推理过程和最后的结果都不是很直观,但我们可以理解是因子节点传递给变量节点的信息,这包括除该变量节点之外的所有因子节点传递给校验节点的信息。表示为因子节点接收到的信息的乘积乘上因子节点本身的约束函数后求和。
是变量节点传递给因子节点的信息,这表现为接收到的其他变量节点信息的乘积
整理自 http://dataunion.org/12187.html