单源最短路径--Dijkstra算法&Bellman_Ford算法
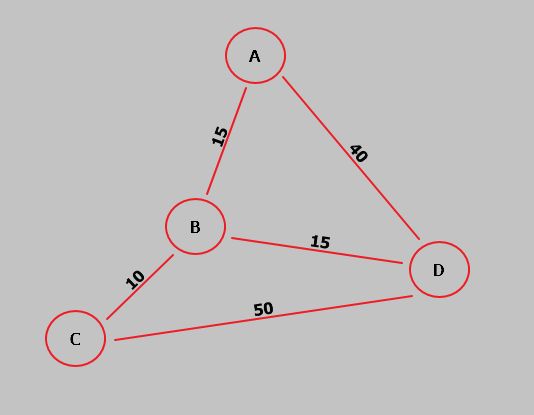
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。形象点,如下图,假如有4个城镇A,B,C,D,它们之间有道路连通,且有长度。现在给定城镇A,求分别到其他城镇B,C,D的最短距离。正如下图,
A到B,C,D的最短路径为:
A--B 15A--B--C 25
A--B--D 30
1)最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
2)Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
二:代码
#include<iostream>
#include<string.h>
#include<stack>
using namespace std;
int* dist; //dist[i]记录源顶点到i的最短距离
int* path; //path[i]记录从源顶点到i路径上的i前面的一个顶点
struct Graph
{
int matrix[10][10]; //邻接矩阵
int vertexNum; //顶点数
int sideNum; //边数
};
void Dijkstra(Graph & graph, int & source);
void ShowPath(Graph & graph, int & source, int v);
int main()
{
/*
5 7
0 1 100
0 2 30
0 4 10
2 1 60
2 3 60
3 1 10
4 3 50
0
*/
Graph graph;
memset(graph.matrix, 0, sizeof(graph.matrix));
cout << "请输入图的顶点数和边数:\n";
cin >> graph.vertexNum >> graph.sideNum;//输入顶点数和边数
dist = new int[graph.vertexNum];//内存申请
path = new int[graph.vertexNum];
int x, y, w;
cout << "请输入边的关系和权值:\n";
for (int i = 0; i < graph.sideNum; i++)
{
cin >> x >> y >> w;//输入边的关系和权值
graph.matrix[x][y] = w;
graph.matrix[y][x] = w;
}
cout << "\n请输入源顶点:\n";
int source;
cin >> source;//输入源顶点
Dijkstra(graph, source);//求出源顶点source到其他顶点的最短路径
for (int i = 0; i < graph.vertexNum; i++)
{
if (i != source)
{
ShowPath(graph, source, i);//输出源顶点source到其他顶点i的最短路径
cout << " 最短路径长度为:" << dist[i] << endl;
}
}
delete[]dist;
delete[]path;
return 0;
}
void Dijkstra(Graph & graph, int & source)
{
bool* visited = new bool[graph.vertexNum];
path[source] = source;
dist[source] = 0;
for (int i = 0; i < graph.vertexNum; i++)//初始化dist,path,visited数组
{
visited[i] = false;
if (graph.matrix[source][i]>0 && i != source)//若源顶点source与i直接邻接
{
dist[i] = graph.matrix[source][i];
path[i] = source;
}
else//若不是直接邻接,dist置为无穷大
{
dist[i] = INT_MAX;
path[i] = -1;
}
}
visited[source] = true;
for (int i = 0; i < graph.vertexNum - 1; i++)//找出除source外剩下的点的最短路径
{
int min = INT_MAX;
int minPos;
for (int j = 0; j < graph.vertexNum; j++)//找到权值最小的点
{
if (!visited[j] && dist[j] < min)
{
min = dist[j];
minPos = j;
}
}
visited[minPos] = true;
for (int k = 0; k < graph.vertexNum; k++)//更新dist数组,路径的值
{
if (!visited[k] && graph.matrix[minPos][k]>0 && graph.matrix[minPos][k] + min < dist[k])
{
dist[k] = graph.matrix[minPos][k] + min;
path[k] = minPos;
}
}
}
delete[]visited;
}
void ShowPath(Graph & graph, int & source, int v)
{
stack<int> s;
cout << "顶点 " << source << " 到顶点 " << v << " 的最短路径是: ";
while (source != v)
{
s.push(v);
v = path[v];
}
cout << source;
while (!s.empty())
{
cout << "--" << s.top();
s.pop();
}
}
三:数据测试
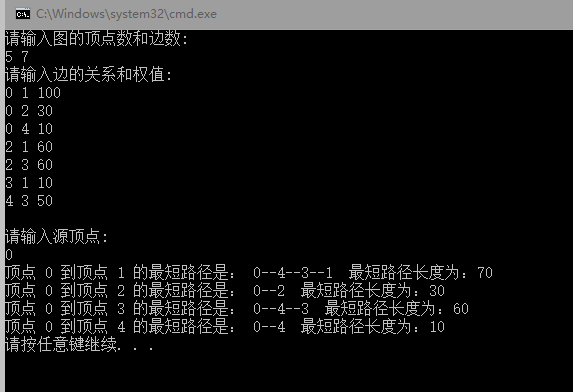
输入数据构建下图:
输出结果:
四:拓展
仔细思考发现上述的Dijkstra算法有个巨大的缺陷,就是图中的边不能有负权。因为当权值可以为负时,可能在图中会存在负权回路,最短路径只要无限次地走这个负权回路,便可以无限制地减少它的最短路径权值,这就变相地说明最短路径不存在,Dijkstra算法无法终止。下图说明从u到v的最短路径是不存在的。那么,应该用什么方法求解?
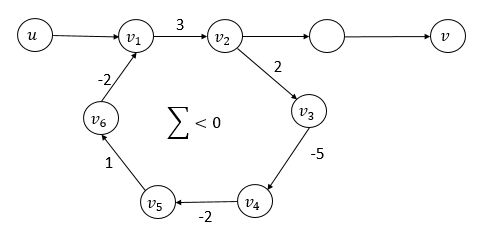
上面我们说Dijkstra算法无法终止,我们可能会想,可不可以试图让Dijkstra算法终止呢?当Dijkstra算法运行时,突然找到了一个负权回路,这下糟糕做不下去了,那么赶快终止算法跳出循环,报告给我们:我找到了负权回路。这个想法是很好的,但是如何判断碰到负权回路是个问题,读者有兴趣可以去实践一下。为了处理存在负权边的情况,我们采用另外一种非常著名的方法:Bellman_Ford算法。
五:Bellman_Ford算法讲解
Dijkstra算法是处理单源最短路径的有效算法,但它局限于边的权值非负的情况,若图中出现权值为负的边,Dijkstra算法就会失效,求出的最短路径就可能是错的。这时候,就需要使用其他的算法来求解最短路径,Bellman-Ford算法就是其中最常用的一个。该算法由美国数学家理查德•贝尔曼(Richard Bellman, 动态规划的提出者)和小莱斯特•福特(Lester Ford)发明。
Bellman-Ford算法的流程如下:
给定图G(V, E)(其中V、E分别为图G的顶点集与边集),源点s,数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为, Distant[s]为0;以下操作循环执行至多n-1次,n为顶点数:对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值;
若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。否则执行下次循环;为了检测图中是否存在负环路,即权值之和小于0的环路。对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。可知,Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E)。
代码如下:
#include<iostream>
#include<stack>
using namespace std;
#define MAX 10000 //假设权值最大不超过10000
struct Edge
{
int u;
int v;
int weight;
};
Edge* edge; //所有边的集合
int* dist; //dist[i]记录源顶点到i的最短距离
int* path; //path[i]记录从源顶点到i路径上的i前面的一个顶点
int nodeNum; //顶点数
int edgeNum; //边数
int original; //源点
bool BellmanFord()
{
for (int i = 0; i < nodeNum; i++)
dist[i] = (i == original) ? 0 : MAX;
for (int i = 1; i <= nodeNum - 1; i++)
{
for (int j = 0; j < edgeNum; j++)
{
if (dist[edge[j].v]>dist[edge[j].u] + edge[j].weight)
{
dist[edge[j].v] = dist[edge[j].u] + edge[j].weight;
path[edge[j].v] = edge[j].u;
}
}
}
bool flag = true;//标记是否有负权回路
for (int i = 0; i < edgeNum; i++)//判断是否有负权回路
{
if (dist[edge[i].v]>dist[edge[i].u] + edge[i].weight)
{
flag = false;
break;
}
}
return flag;
}
void Print()
{
for (int i = 0; i < nodeNum; i++)
{
if (i != original)
{
int p = i;
stack<int> s;
cout << "顶点 " << original << " 到顶点 " << p << " 的最短路径是: ";
while (original != p)
{
s.push(p);
p = path[p];
}
cout << original;
while (!s.empty())
{
cout << "--" << s.top();
s.pop();
}
cout << " 最短路径长度是:" << dist[i] << endl;
}
}
}
int main()
{
/*
------------case 1:
5 7 0
0 1 100
0 2 30
0 4 10
2 1 60
2 3 60
3 1 10
4 3 50
-----------case 2:
4 6 0
0 1 20
0 2 5
3 0 -200
1 3 4
3 1 4
2 3 2
*/
cout << "请输入图的顶点数,边数,源点:";
cin >> nodeNum >> edgeNum >> original;
dist = new int[nodeNum];
path = new int[nodeNum];
edge = new Edge[edgeNum];
cout << "请输入" << edgeNum << "条边的信息:\n";
for (int i = 0; i < edgeNum; i++)
cin >> edge[i].u >> edge[i].v >> edge[i].weight;
if (BellmanFord())
Print();
else
cout << "Sorry,it have negative circle!\n";
return 0;
}
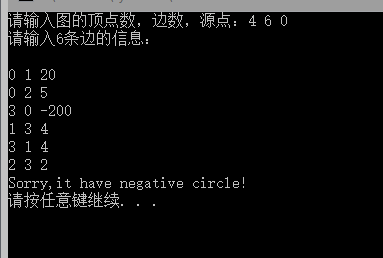
两组数据测试如下图:
参考:http://blog.csdn.net/niushuai666/article/details/6791765