若干最小路径覆盖问题
Taxi Cab Scheme
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 5964 | Accepted: 2502 |
Description
Running a taxi station is not all that simple. Apart from the obvious demand for a centralised coordination of the cabs in order to pick up the customers calling to get a cab as soon as possible,there is also a need to schedule all the taxi rides which have been booked in advance.Given a list of all booked taxi rides for the next day, you want to minimise the number of cabs needed to carry out all of the rides.
For the sake of simplicity, we model a city as a rectangular grid. An address in the city is denoted by two integers: the street and avenue number. The time needed to get from the address a, b to c, d by taxi is |a - c| + |b - d| minutes. A cab may carry out a booked ride if it is its first ride of the day, or if it can get to the source address of the new ride from its latest,at least one minute before the new ride's scheduled departure. Note that some rides may end after midnight.
For the sake of simplicity, we model a city as a rectangular grid. An address in the city is denoted by two integers: the street and avenue number. The time needed to get from the address a, b to c, d by taxi is |a - c| + |b - d| minutes. A cab may carry out a booked ride if it is its first ride of the day, or if it can get to the source address of the new ride from its latest,at least one minute before the new ride's scheduled departure. Note that some rides may end after midnight.
Input
On the first line of the input is a single positive integer N, telling the number of test scenarios to follow. Each scenario begins with a line containing an integer M, 0 < M < 500, being the number of booked taxi rides. The following M lines contain the rides. Each ride is described by a departure time on the format hh:mm (ranging from 00:00 to 23:59), two integers a b that are the coordinates of the source address and two integers c d that are the coordinates of the destination address. All coordinates are at least 0 and strictly smaller than 200. The booked rides in each scenario are sorted in order of increasing departure time.
Output
For each scenario, output one line containing the minimum number of cabs required to carry out all the booked taxi rides.
Sample Input
2 2 08:00 10 11 9 16 08:07 9 16 10 11 2 08:00 10 11 9 16 08:06 9 16 10 11
Sample Output
1 2
poj2060:每个任务有起点和终点，当完成自身任务，又从终点到下一个地点的起点，若曼哈顿距离之和小于该车的时间说明这辆车可以完成这两个任务，于是就连边。本题就是最小路径覆盖问题，化归为|V|-二分图的最大匹配。
代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#define Maxn 510
using namespace std;
struct point{
int m,sx,sy,ex,ey;
}p[Maxn];
int dis(int x1,int y1,int x2,int y2){
return abs(x1-x2)+abs(y1-y2);
}
int adj[Maxn][Maxn];
int match[Maxn];
int vis[Maxn];
int x,y;
int deep;
bool dfs(int u){
for(int v=1;v<=y;v++){
if(adj[u][v]&&vis[v]!=deep){
vis[v]=deep;
if(match[v]==-1||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int hungary(){
memset(match,-1,sizeof match);
memset(vis,-1,sizeof vis);
int ans=0;
for(int i=1;i<=x;i++){
deep=i;
if(dfs(i)) ans++;
}
return ans;
}
int main()
{
int t,a,b;
cin>>t;
while(t--){
cin>>x;
y=x;
for(int i=1;i<=x;i++){
scanf("%d:%d%d%d%d%d",&a,&b,&p[i].sx,&p[i].sy,&p[i].ex,&p[i].ey);
p[i].m=a*60+b;
}
memset(adj,0,sizeof adj);
for(int i=1;i<=x;i++)
for(int j=i+1;j<=x;j++){
int d1=dis(p[i].sx,p[i].sy,p[i].ex,p[i].ey),
d2=dis(p[i].ex,p[i].ey,p[j].sx,p[j].sy);
if(d1+d2<p[j].m-p[i].m) adj[i][j]=1;
}
printf("%d\n",x-hungary());
}
return 0;
}
poj2594可重点的最小路径覆盖，这个只要用floyd预处理两点是否可达，然后求普通的最小路径覆盖即可。
Treasure Exploration
| Time Limit: 6000MS | Memory Limit: 65536K | |
| Total Submissions: 6991 | Accepted: 2843 |
Description
Have you ever read any book about treasure exploration? Have you ever see any film about treasure exploration? Have you ever explored treasure? If you never have such experiences, you would never know what fun treasure exploring brings to you.
Recently, a company named EUC (Exploring the Unknown Company) plan to explore an unknown place on Mars, which is considered full of treasure. For fast development of technology and bad environment for human beings, EUC sends some robots to explore the treasure.
To make it easy, we use a graph, which is formed by N points (these N points are numbered from 1 to N), to represent the places to be explored. And some points are connected by one-way road, which means that, through the road, a robot can only move from one end to the other end, but cannot move back. For some unknown reasons, there is no circle in this graph. The robots can be sent to any point from Earth by rockets. After landing, the robot can visit some points through the roads, and it can choose some points, which are on its roads, to explore. You should notice that the roads of two different robots may contain some same point.
For financial reason, EUC wants to use minimal number of robots to explore all the points on Mars.
As an ICPCer, who has excellent programming skill, can your help EUC?
Recently, a company named EUC (Exploring the Unknown Company) plan to explore an unknown place on Mars, which is considered full of treasure. For fast development of technology and bad environment for human beings, EUC sends some robots to explore the treasure.
To make it easy, we use a graph, which is formed by N points (these N points are numbered from 1 to N), to represent the places to be explored. And some points are connected by one-way road, which means that, through the road, a robot can only move from one end to the other end, but cannot move back. For some unknown reasons, there is no circle in this graph. The robots can be sent to any point from Earth by rockets. After landing, the robot can visit some points through the roads, and it can choose some points, which are on its roads, to explore. You should notice that the roads of two different robots may contain some same point.
For financial reason, EUC wants to use minimal number of robots to explore all the points on Mars.
As an ICPCer, who has excellent programming skill, can your help EUC?
Input
The input will consist of several test cases. For each test case, two integers N (1 <= N <= 500) and M (0 <= M <= 5000) are given in the first line, indicating the number of points and the number of one-way roads in the graph respectively. Each of the following M lines contains two different integers A and B, indicating there is a one-way from A to B (0 < A, B <= N). The input is terminated by a single line with two zeros.
Output
For each test of the input, print a line containing the least robots needed.
Sample Input
1 0 2 1 1 2 2 0 0 0
Sample Output
1 1 2
代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#define Maxn 510
using namespace std;
int adj[Maxn][Maxn];
int match[Maxn];
int vis[Maxn];
int x,y;
int deep;
bool dfs(int u){
for(int v=1;v<=y;v++){
if(adj[u][v]&&vis[v]!=deep){
vis[v]=deep;
if(match[v]==-1||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int hungary(){
memset(match,-1,sizeof match);
memset(vis,-1,sizeof vis);
int ans=0;
for(int i=1;i<=x;i++){
deep=i;
if(dfs(i)) ans++;
}
return ans;
}
int main()
{
int n,m,a,b;
while(cin>>n>>m,n){
memset(adj,0,sizeof adj);
for(int i=0;i<m;i++){
cin>>a>>b;
adj[a][b]=1;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
adj[i][j]=adj[i][j]|adj[i][k]&adj[k][j];
x=y=n;
printf("%d\n",n-hungary());
}
return 0;
}
poj1548最小路径覆盖，对于满足p[i].x<=p[j].x&&p[i].y<=p[j].y这个条件的i,j建一条i指向j的边。
Robots
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3970 | Accepted: 1810 |
Description
Your company provides robots that can be used to pick up litter from fields after sporting events and concerts. Before robots are assigned to a job, an aerial photograph of the field is marked with a grid. Each location in the grid that contains garbage is marked. All robots begin in the Northwest corner and end their movement in the Southeast corner. A robot can only move in two directions, either to the East or South. Upon entering a cell that contains garbage, the robot will pick it up before proceeding. Once a robot reaches its destination at the Southeast corner it cannot be repositioned or reused. Since your expenses are directly proportional to the number of robots used for a particular job, you are interested in finding the minimum number of robots that can clean a given field. For example, consider the field map shown in Figure 1 with rows and columns numbered as shown and garbage locations marked with a 'G'. In this scheme, all robots will begin in location 1,1 and end in location 6, 7.
Figure 1 - A Field Map
Figure 2 below shows two possible solutions, the second of which is preferable since it uses two robots rather than three.
Figure 2 - Two Possible Solutions
Your task is to create a program that will determine the minimum number of robots needed to pick up all the garbage from a field.
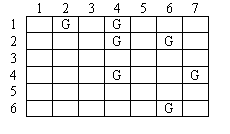
Figure 1 - A Field Map
Figure 2 below shows two possible solutions, the second of which is preferable since it uses two robots rather than three.
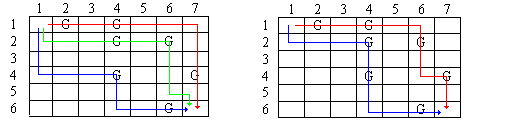
Figure 2 - Two Possible Solutions
Your task is to create a program that will determine the minimum number of robots needed to pick up all the garbage from a field.
Input
The input consists of one or more field maps followed by a line containing -1 -1 to signal the end of the input data. A field map consists of one or more lines, each containing one garbage location, followed by a line containing 0 0 to signal the end of the map. Each garbage location consists of two integers, the row and column, separated by a single space. The rows and columns are numbered as shown in Figure 1. The garbage locations will be given in row-major order. No single field map will have more than 24 rows and 24 columns. The sample input below shows an input file with two field maps. The first is the field map from Figure 1.
Output
The output will consist of a single line for each field map containing the minimum number of robots needed to clean the corresponding field.
Sample Input
1 2 1 4 2 4 2 6 4 4 4 7 6 6 0 0 1 1 2 2 4 4 0 0 -1 -1
Sample Output
2 1
代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#define Maxn 25*25
using namespace std;
struct point{
int x,y;
point(){}
point(int xx,int yy):x(xx),y(yy){}
bool operator<(const point &a)const{
return x<=a.x&&y<=a.y;
}
}p[Maxn];
int adj[Maxn][Maxn];
int match[Maxn];
int vis[Maxn];
int x,y;
int deep;
bool dfs(int u){
for(int v=1;v<=y;v++){
if(adj[u][v]&&vis[v]!=deep){
vis[v]=deep;
if(match[v]==-1||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int hungary(){
memset(match,-1,sizeof match);
memset(vis,-1,sizeof vis);
int ans=0;
for(int i=1;i<=x;i++){
deep=i;
if(dfs(i)) ans++;
}
return ans;
}
int main()
{
int a,b;
while(cin>>a>>b,a!=-1){
if(!a) break;
int tot=0;
p[++tot]=point(a,b);
while(cin>>a>>b,a){
p[++tot]=point(a,b);
}
memset(adj,0,sizeof adj);
for(int i=1;i<=tot;i++)
for(int j=i+1;j<=tot;j++)
if(p[i]<p[j])
adj[i][j]=1;
x=y=tot;
printf("%d\n",tot-hungary());
}
return 0;
}
poj3216最小路径覆盖，以每个任务作为节点建图，首先用floyd预处理各点之间的最短路mat，然后若满足p[i].d+p[i].t+mat[i][j]<=p[j].d这个条件，说明完成i任务后可赶赴j任务，于是将i+1到j+1连一条边，+1是为了保证几点从1开始。
Repairing Company
| Time Limit: 1000MS | Memory Limit: 131072K | |
| Total Submissions: 6446 | Accepted: 1730 |
Description
Lily runs a repairing company that services the Q blocks in the city. One day the company receives M repair tasks, the ith of which occurs in block pi, has a deadline ti on any repairman’s arrival, which is also its starting time, and takes a single repairman di time to finish. Repairmen work alone on all tasks and must finish one task before moving on to another. With a map of the city in hand, Lily want to know the minimum number of repairmen that have to be assign to this day’s tasks.
Input
The input contains multiple test cases. Each test case begins with a line containing Q and M (0 < Q ≤ 20, 0 < M ≤ 200). Then follow Q lines each with Q integers, which represent a Q × Q matrix Δ = {δij}, where δij means a bidirectional road connects the ith and the jth blocks and requires δij time to go from one end to another. If δij = −1, such a road does not exist. The matrix is symmetric and all its diagonal elements are zeroes. Right below the matrix are M lines describing the repairing tasks. The ith of these lines contains pi, ti and di. Two zeroes on a separate line come after the last test case.
Output
For each test case output one line containing the minimum number of repairmen that have to be assigned.
Sample Input
1 2 0 1 1 10 1 5 10 0 0
Sample Output
2
代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#define Maxn 210
using namespace std;
struct point{
int id,d,t;
}p[Maxn];
int adj[Maxn][Maxn];
int match[Maxn];
int vis[Maxn];
int x,y;
int deep;
bool dfs(int u){
for(int v=1;v<=y;v++){
if(adj[u][v]&&vis[v]!=deep){
vis[v]=deep;
if(match[v]==-1||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int hungary(){
memset(match,-1,sizeof match);
memset(vis,-1,sizeof vis);
int ans=0;
for(int i=1;i<=x;i++){
deep=i;
if(dfs(i)) ans++;
}
return ans;
}
const int inf=0x3f3f3f3f;
int mat[Maxn][Maxn];
int main()
{
int n,m;
while(cin>>n>>m,n){
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
cin>>mat[i][j];
if(mat[i][j]==-1) mat[i][j]=inf;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
mat[i][j]=min(mat[i][j],mat[i][k]+mat[k][j]);
for(int i=0;i<m;i++){
cin>>p[i].id>>p[i].d>>p[i].t;
}
memset(adj,0,sizeof adj);
for(int i=0;i<m;i++)
for(int j=0;j<m;j++)
if(i!=j&&p[i].d+p[i].t+mat[p[i].id][p[j].id]<=p[j].d){
adj[i+1][j+1]=1;
}
x=y=m;
printf("%d\n",m-hungary());
}
return 0;
}