POJ2528Mayor's posters（离散化 + 线段树）

题目链接：

题意：给定一些高度都相同的海报去贴，问最后能看见几张海报

The picture below illustrates the case of the sample input.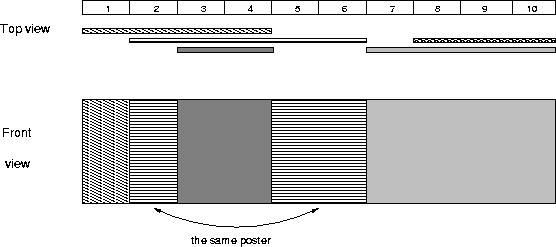

{ 8,9,10}那张被覆盖看不到，

分析：看了大神们的博客大神是一看就是线段树，可是我都知道是线段树了也不知道怎么做，真是弱的一逼；

线段树分析就是对于每一个海报所在的区间设置一个不同的数字，然后就统计有几个不同的数字即所求解，就是线段树区间更改

技巧：离散化

如果按照这个墙的宽度来设置线段树的话，很大，内存会超。考虑到海报的个数不会很多，所以根据海报的区间的两个端点来进行离散处理，

拿例子来说，{1,4} {2,6} {8,10} {3,4} {7，10} ，所以需要的点为 1， 2， 3， 4， 6， 7， 8 ，10，令x[1] = 1, x[2] = 2，x[3] = 3，x[4] = 4，x[5] = 6，x[6] = 7,x[7] = 8, x[8] = 10，就将原来大的 【 1,10】区间变成了【1,8】这就是离散化

还有一个bug，如果这组样例： {1,10} {1,3} {5,10} 就离散成了 x[1] = 1, x[2] = 3, x[3] = 5, x[4] = 10,

第一张海报时候{1,10}，对于离散化后的处理时，{1,4}

第二张{1,3}， 对于离散化后的就是{1,2}

第三张{5,10}，对于离散化后的就是{3,4}

对于离散化后的来统计，最后结果是2，而实际确实3，原因就是 3到5之间有4而离散化之后就把4给去掉了，这就是一个bug,处理方法就是把相邻的两个数如果差大于1就在添加一个数

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <cstring>
  4 #include <cstdio>
  5 using namespace std;
  6 const int Max = 100000; //根据海报的个数来设置数组
  7 struct node
  8 {
  9     int l,r;
 10     int cover; //海报的编号
 11     int tag;  //懒惰标志
 12 };
 13 node tree[Max * 8];
 14 int t[4 * Max + 10],cnt,res[Max * 4 + 10];
 15 int a[Max + 10],b[Max + 10];
 16 void buildTree(int left, int right, int k)
 17 {
 18     tree[k].l = left;
 19     tree[k].r = right;
 20     tree[k].cover = 0;
 21     tree[k].tag = -1;
 22     if(left == right)
 23         return;
 24     int mid = (left + right) / 2;
 25     buildTree(left, mid, k * 2);
 26     buildTree(mid + 1, right, k * 2 + 1);
 27 }
 28 int Find(int l, int r, int key, int temp[])
 29 {
 30     while(r >= l)
 31     {
 32         int mid = (l + r) / 2;
 33         if(temp[mid] == key)
 34             return mid;
 35         else if(temp[mid] > key)
 36         {
 37             r = mid - 1;
 38         }
 39         else
 40         {
 41             l = mid + 1;
 42         }
 43     }
 44     return -1;
 45 }
 46 void upDate(int left, int right, int k, int num)
 47 {
 48     if(tree[k].l == left && tree[k].r == right)
 49     {
 50         tree[k].cover = num;
 51         tree[k].tag = num;
 52         return;
 53     }
 54     if(tree[k].tag != -1)
 55     {
 56         tree[k * 2].tag = tree[k * 2 + 1].tag = tree[k].tag;
 57         tree[k * 2].cover = tree[k * 2 + 1].cover = tree[k].tag;
 58         tree[k].tag = -1;
 59     }
 60     int mid = (tree[k].l + tree[k].r) / 2;
 61     if(right <= mid)
 62     {
 63         upDate(left, right, k * 2, num);
 64     }
 65     else if(mid < left)
 66     {
 67         upDate(left, right, k * 2 + 1, num);
 68     }
 69     else
 70     {
 71         upDate(left, mid, k * 2, num);
 72         upDate(mid + 1, right, k * 2 + 1, num);
 73     }
 74 }
 75 void Search(int k)
 76 {
 77     if(tree[k].tag != -1)
 78     {
 79         tree[k].cover = tree[k].tag;
 80         tree[k * 2].tag = tree[k * 2 + 1].tag = tree[k].tag;
 81         tree[k * 2].cover = tree[k * 2 + 1].cover = tree[k].tag;
 82         tree[k].tag = -1;
 83     }
 84 
 85     if(tree[k].l == tree[k].r)
 86     {
 87         res[ tree[k].cover ] = 1; // 看看每一个点的海报编号
 88         return;
 89     }
 90     Search(k * 2);
 91     Search(k * 2 + 1);
 92 }
 93 int main()
 94 {
 95     int test,n;
 96     scanf("%d", &test);
 97     while(test--)
 98     {
 99         scanf("%d", &n);
100         cnt = 0;
101         for(int i = 1; i <= n; i++)
102         {
103             scanf("%d%d", &a[i], &b[i]);
104             t[ cnt++ ] = a[i];
105             t[ cnt++ ] = b[i]; //将所有的端点都放入t中
106         }
107         sort(t, t + cnt);
108         int cnt1 = 1;
109         for(int i = 1; i < cnt; i++)
110         {
111             if(t[i] != t[i - 1])  //去掉相同的
112                 t[ cnt1++ ] = t[i];
113         } 
114         for(int i = cnt1 - 1; i > 0; i--)
115         {
116             if(t[i] - t[i - 1] > 1) //如果相邻数差值大于1，就则加一个数
117                 t[ cnt1++ ] = t[i - 1] + 1;
118         }
119         sort(t, t + cnt1); //加完之后排序，此时已经离散完毕
120         for(int i = cnt1; i > 0; i--)
121             t[i] = t[i - 1];
122         //使区间为1到cnt1，好处理
123         buildTree(1, cnt1, 1);
124 
125         for(int i = 1; i <= n; i++)
126         {
127             int left = Find(1, cnt1, a[i], t);  //二分查找出每个区间的端点在离散化后的数组中的位置
128             int right = Find(1, cnt1, b[i], t);
129             upDate(left, right, 1, i);  //更新，设置覆盖位为 i
130         }
131         memset(res, 0, sizeof(res));
132         Search(1); //从根开始查找
133         int ans = 0;
134         for(int i = 1; i <= n; i++)
135             if(res[i])
136             ans++;
137         printf("%d\n", ans);
138     }
139     return 0;
140 }

View Code