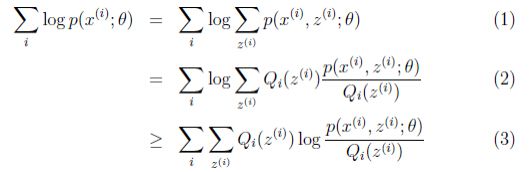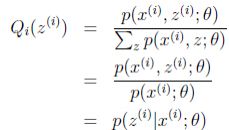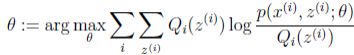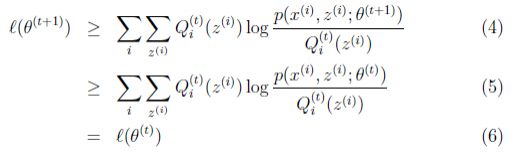EM算法
内推群里面大家都收到电话面试了，估计我简历又挂了吧0.0。命中有时终须有，命中无时莫强求。一切尽人事听天命，随缘。这波结束之后是时候好好修改修改简历了。
好啦，下面谈谈EM算法。关于前两篇博文http://blog.csdn.net/lvhao92/article/details/50788380和http://blog.csdn.net/lvhao92/article/details/50802703为本篇做了个大铺垫。都说了一下EM算法的应用。同学们想必也大体上了解了EM算法是个什么东东，具体怎么的去运用。其实，个人认为这已经足够了。这篇博文为了EM的完整性，再多啰嗦点EM.
但凡提到EM算法。必先提及Jensen不等式。看图
即若f函数为凸函数。那么会满足
。
若f函数为凹函数，那么就会满足
。直接从图上不就可以看出来这个关系了吧，这个式子有什么用？跟EM算法有什么关系呢？且往下看
我们首先假设训练样本我们要找到每个样例的隐类别Z（反观之前两个例子，都是非监督，因此类别Z是未知的，是隐含参数），θ表示模型的参数。
首先，对θ做极大似然估计，那么应该最大化对数似然
可以发现由于隐参数Z的存在，直接求θ的极大似然比较困难。咋办呢？
只有采用鸡蛋悖论，迭代了。若参数θ已知，则可根据训练数据推断出最优隐变量Z的值(E步)；反之，若Z的值已知，则可以联合观测变量X一起对参数θ进行极大似然估计(M步)。
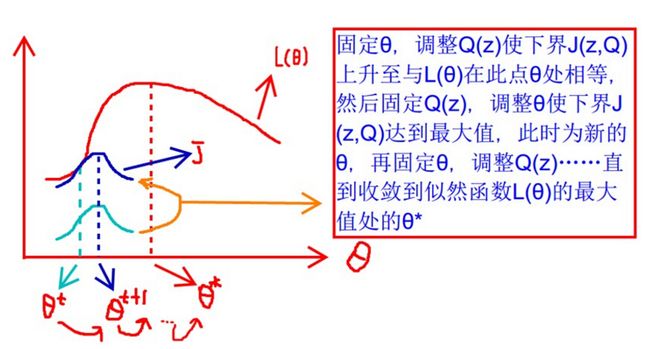
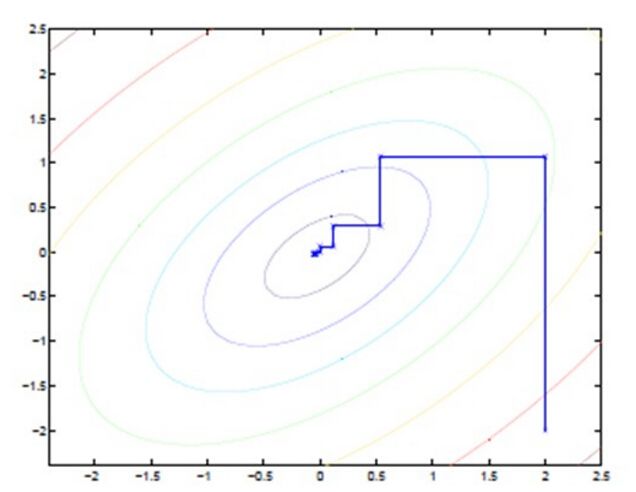
恩，也可以从下界的思路去理解。盗一个前辈的图(懒得画了)
其中提到的Qi(z)就是对于每一个样例i，让Qi表示该样例隐含变量z的某种分布。
，比如要将班上的学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布，如果按照隐藏变量是男女，那么就是伯努利分布。
前辈的图画的非常的好，道理也讲得很清楚，鄙人实在是佩服。再做点解析，EM分为不断建立l的下界(E步)，然后优化下界(M步)。看上面的图，由浅蓝到深蓝就是调整下界，使得下界不断上升的过程，前辈说是不断调整Q(z)，其实这里说是联合调整Q(z)和p(x,z|θ)更合适（下面会给出数学说明），这里参数θ由M步得到，假装已知。而由θt变成θ(t+1)这个过程就是根据观测变量X和隐藏变量Z来调整参数的过程(隐藏变量Z由E步得到，假装已知)。对下界进行一个优化。
注意的是这里下界图中是一个凸函数，而数学表达式上就是一个式子。（讲到那儿的时候我会特别强调，不然会弄不懂逻辑关系）
(1)式就是我们需要最大化的似然公式，(2)式就是将其分子分母同时承隐变量Z的概率分布。重点就是(3)式，(3)式就是之前所说的下界，就是EM算法围绕的一个东西，E步的时候是创建了它，如上所示，而M步的时候则是需要优化它，后面再说。
那这个式子怎么来的呢？我们先来看(2)式中的。等等，这不就是
的期望吗？
期望怎么来的？
令Y为，Qi(z)为pk。所以就可以说明(2)试中的就是的期望。
那不就是E(Y)么，那么(2)式可以表现成f(E(y))，那根据前面的jeason公式，由于我们的log是凹函数，不就是大于等于E(f(y))吗？那不就是（3）式吗？
所以我们已经可以表示出下界了。那就是(3)式。那么接下来就要进行E步，对下界进行调整，使它不断上升，从图上的浅蓝到深蓝，我们希望它能在θ处与l(θ)相等，不就是要使得上面的(3)式和(1)式相等吗？不就是使得这个不等号变成等号吗？那什么时候才能取等号呢？
jeason不等式取等式，需要让随机变量变成常数值。得到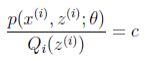
。我们之前不是有假设么~这样的话，
（多个等式分子分母相加不变）
所以可以得到式子
（将这个式子，带入，然后变化一下就可以得到）
所以在固定参数θ之后，我们的Qi(Z)终于千呼万唤死出来，就是后验概率，E步完结！
下面说M步，前面也提到，M步就是固定Q(z)之后，调整下界，调整θ，极大化l(θ)的下界。
M步就是
。
好了，M步完结。EM算法就这么说完了。
接下来扯点啥？你要问EM算法收敛吗？
那么下面就是证明我们的EM算法是收敛滴
如果我们能证明
，说明极大似然估计在单调增加，说明最终我们会达到最大似然估计的最大值，说明这是收敛的。
好，故事发生在M步，由θ(t)到θ(t+1)的过程中。发生了下面(4)(5)(6)这样的事。从结果上来看，已经证明了。下面详细介绍。
(4)步就是前面E步的(3)。(5)步就是M的过程中，调整θ，肯定是要使这个下界变大的。M步不就是极大化这个下界吗？！
(6)步。哥们，我们现在都是处理θ(t+1)的M步了，那么θ(t)的E步肯定是已经完成的啦。既然完成那这个等号不应该存在吗？！(jeason取等号，也就是θ(t)的E步)
好了，证明完毕。
可以发现。
EM不就是固定θ，优化Q。然后固定Q，优化θ么。我们之前称它为鸡蛋搞基。但是这个思想也可以看成是J的坐标上升法的。
完！
周六的夜晚果真不适合写博客
开撸！