【leetcode】【22】Generate Parentheses
一、问题描述
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
"((()))", "(()())", "(())()", "()(())", "()()()"
二、问题分析
这是一个典型的backtracking问题,关于backtracking
Backtracking is a form of recursion.
The usual scenario is that you are faced with a number of options, and you must choose one of these. After you make your choice you will get a new set of options; just what set of options you get depends on what choice you made. This procedure is repeated over and over until you reach a final state. If you made a good sequence of choices, your final state is agoal state; if you didn't, it isn't.
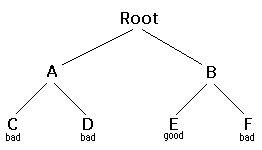
Conceptually, you start at the root of a tree; the tree probably has some good leaves and some bad leaves, though it may be that the leaves are all good or all bad. You want to get to a good leaf. At each node, beginning with the root, you choose one of its children to move to, and you keep this up until you get to a leaf.
Suppose you get to a bad leaf. You can backtrack to continue the search for a good leaf by revoking yourmost recent choice, and trying out the next option in that set of options. If you run out of options, revoke the choice that got you here, and try another choice at that node. If you end up at the root with no options left, there are no good leaves to be found.
This needs an example.
- Starting at Root, your options are A and B. You choose A.
- At A, your options are C and D. You choose C.
- C is bad. Go back to A.
- At A, you have already tried C, and it failed. Try D.
- D is bad. Go back to A.
- At A, you have no options left to try. Go back to Root.
- At Root, you have already tried A. Try B.
- At B, your options are E and F. Try E.
- E is good. Congratulations!
In this example we drew a picture of a tree. The tree is an abstract model of the possible sequences of choices we could make. There is also a data structure called a tree, but usually we don't have a data structure to tell us what choices we have. (If we do have an actual tree data structure, backtracking on it is calleddepth-first tree searching.)
Here is the algorithm (in pseudocode) for doing backtracking from a given node n:
boolean solve(Node n) {
if n is a leaf node {
if the leaf is a goal node, return true
else return false
} else {
for each child c of n {
if solve(c) succeeds, return true
}
return false
}
}
Notice that the algorithm is expressed as a boolean function. This is essential to understanding the algorithm. Ifsolve(n) is true, that means node nis part of a solution--that is, node n is one of the nodes on a path from the root to some goal node. We say that nis solvable. If solve(n) is false, then there is no path that includes n to any goal node.
How does this work?
- If any child of n is solvable, then nis solvable.
- If no child of n is solvable, then nis not solvable.
Hence, to decide whether any non-leaf node nis solvable (part of a path to a goal node), all you have to do is test whether any child of nis solvable. This is done recursively, on each child of n. In the above code, this is done by the lines
for each child c of n {
if solve(c) succeeds, return true
}
return false
Eventually the recursion will "bottom" out at a leaf node. If the leaf node is a goal node, it is solvable; if the leaf node is not a goal node, it is not solvable. This is our base case. In the above code, this is done by the lines
if n is a leaf node {
if the leaf is a goal node, return true
else return false
}
The backtracking algorithm is simple but important. You should understand it thoroughly.
给定的n为括号对,所以就是有n个左括号和n个右括号的组合。
按顺序尝试知道左右括号都尝试完了就可以算作一个解。
注意,左括号的数不能大于右括号,要不然那就意味着先尝试了右括号而没有左括号,类似“)(” 这种解是不合法的。
三、Java AC 代码
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<String>();
if (n <= 0) {
return res;
}
dfsHelper(n, n, new String(), res);
return res;
}
public void dfsHelper(int l, int r, String item, List<String> res) {
if (l > r) {
return;
}
if (l == 0 && r == 0) {
res.add(item);
}
if (l > 0) {
dfsHelper(l - 1, r, item + "(", res);
}
if (r > 0) {
dfsHelper(l, r - 1, item + ")", res);
}
}