复杂数据结构(二)树
线索二叉树
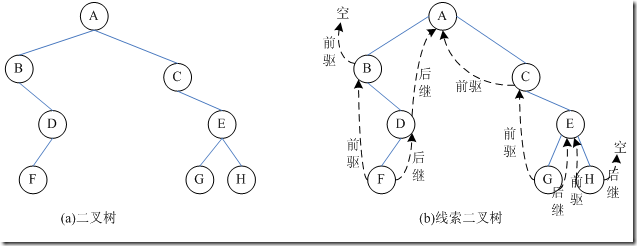
对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
例:中序:B F D A C G E H
线索二叉树结构:二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。现将二叉树的结点结构重新定义如下:
ltag=0 时lchild指向左子女
ltag=1 时lchild指向前驱
rtag=0 时rchild指向右子女
rtag=1 时rchild指向后继
这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
线索二叉树的表示 :
程序实现:
创建线索二叉树
操作线索二叉树
遍历线索二叉树
#include <stdio.h> #include <stdlib.h> #define QUEUE_MAXSIZE 50 typedef char DATA; //定义元素类型 typedef enum { SubTree, Thread }NodeFlag; //枚举值SubTree(子树)和Thread(线索)分别为0,1 typedef struct ThreadTree //定义线索二叉树结点类型 { DATA data; //元素数据 NodeFlag lflag; //左标志 NodeFlag rflag; //右标志 struct ThreadTree *left; //左子树结点指针 struct ThreadTree *right; //右子树结点指针 }ThreadBinTree; ThreadBinTree *Previous=NULL; //前驱结点指针 ThreadBinTree *BinTreeInit(ThreadBinTree *node) //初始化二叉树根结点 { if(node!=NULL) //若二叉树根结点不为空 return node; else return NULL; } int BinTreeAddNode(ThreadBinTree *bt,ThreadBinTree *node,int n) //添加数据到二叉树 //bt为父结点,node为子结点,n=1表示添加左子树,n=2表示添加右子树 { if(bt==NULL) { printf("父结点不存在,请先设置父结点!\n"); return 0; } switch(n) { case 1: //添加到左结点 if(bt->left) //左子树不为空 { printf("左子树结点不为空!\n"); return 0; }else bt->left=node; break; case 2://添加到右结点 if( bt->right) //右子树不为空 { printf("右子树结点不为空!\n"); return 0; }else bt->right=node; break; default: printf("参数错误!\n"); return 0; } return 1; } ThreadBinTree *BinTreeLeft(ThreadBinTree *bt) //返回左子结点 { if(bt) return bt->left; else return NULL; } ThreadBinTree *BinTreeRight(ThreadBinTree *bt) //返回右子结点 { if(bt) return bt->right; else return NULL; } int BinTreeIsEmpty(ThreadBinTree *bt) //检查二叉树是否为空,为空则返回1,否则返回0 { if(bt) return 0; else return 1; } int BinTreeDepth(ThreadBinTree *bt) //求二叉树深度 { int dep1,dep2; if(bt==NULL) return 0; //对于空树,深度为0 else { dep1 = BinTreeDepth(bt->left); //左子树深度 (递归调用) dep2 = BinTreeDepth(bt->right); //右子树深度 (递归调用) if(dep1>dep2) return dep1 + 1; else return dep2 + 1; } } ThreadBinTree *BinTreeFind(ThreadBinTree *bt,DATA data) //在二叉树中查找值为data的结点 { ThreadBinTree *p; if(bt==NULL) return NULL; else { if(bt->data==data) return bt; else{ // 分别向左右子树递归查找 if(p=BinTreeFind(bt->left,data)) return p; else if(p=BinTreeFind(bt->right, data)) return p; else return NULL; } } } void BinTreeClear(ThreadBinTree *bt) // 清空二叉树,使之变为一棵空树 { if(bt) { BinTreeClear(bt->left); //清空左子树 BinTreeClear(bt->right);//清空右子树 free(bt);//释放当前结点所占内存 bt=NULL; } return; } void BinTree_DLR(ThreadBinTree *bt,void (*oper)(ThreadBinTree *p)) //先序遍历 { if(bt)//树不为空,则执行如下操作 { oper(bt); //处理结点的数据 BinTree_DLR(bt->left,oper); BinTree_DLR(bt->right,oper); } return; } void BinTree_LDR(ThreadBinTree *bt,void(*oper)(ThreadBinTree *p)) //中序遍历 { if(bt)//树不为空,则执行如下操作 { BinTree_LDR(bt->left,oper); //中序遍历左子树 oper(bt);//处理结点数据 BinTree_LDR(bt->right,oper); //中序遍历右子树/ } return; } void BinTree_LRD(ThreadBinTree *bt,void (*oper)(ThreadBinTree *p)) //后序遍历 { if(bt) { BinTree_LRD(bt->left,oper); //后序遍历左子树 BinTree_LRD(bt->right,oper); //后序遍历右子树/ oper(bt); //处理结点数据 } return; } void BinTree_Level(ThreadBinTree *bt,void (*oper)(ThreadBinTree *p)) //按层遍历 { ThreadBinTree *p; ThreadBinTree *q[QUEUE_MAXSIZE]; //定义一个顺序栈 int head=0,tail=0;//队首、队尾序号 if(bt)//若队首指针不为空 { tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列队尾序号 q[tail] = bt;//将二叉树根指针进队 } while(head!=tail) //队列不为空,进行循环 { head=(head+1)%QUEUE_MAXSIZE; //计算循环队列的队首序号 p=q[head]; //获取队首元素 oper(p);//处理队首元素 if(p->left!=NULL) //若结点存在左子树,则左子树指针进队 { tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列的队尾序号 q[tail]=p->left;//将左子树指针进队 } if(p->right!=NULL)//若结点存在右孩子,则右孩子结点指针进队 { tail=(tail+1)%QUEUE_MAXSIZE;//计算循环队列的队尾序号 q[tail]=p->right;//将右子树指针进队 } } return; } void BinTreeThreading_LDR(ThreadBinTree *bt) //二叉树按中序线索化 { if(bt) //结点非空时,当前访问结点 { BinTreeThreading_LDR(bt->left); //递归调用,将左子树线索化 bt->lflag=(bt->left)?SubTree:Thread; //设置左指针域的标志 bt->rflag=(bt->right)?SubTree:Thread;//设置右指针域的标志 if(Previous) //若当前结点的前驱Previous存在 { if(Previous->rflag==Thread) //若当前结点的前驱右标志为线索 Previous->right=bt;//设Previous的右线索指向后继 if(bt->lflag==Thread) //若当前结点的左标志为线索 bt->left=Previous;//设当前结点的左线索指向中序前驱 } Previous=bt;//让Previous保存刚访问的结点 BinTreeThreading_LDR(bt->right);//递归调用,将右子树线索化 } } ThreadBinTree *BinTreeNext_LDR(ThreadBinTree *bt) //求指定结点的后继 { ThreadBinTree *nextnode; if(!bt) return NULL; //若当前结点为空,则返回空 if(bt->rflag==Thread) //若当前结点的右子树为空 return bt->right; //返回右线索所指的中序后继 else{ nextnode=bt->right; //从当前结点的右子树开始查找 while(nextnode->lflag==SubTree) //循环处理所有左子树不为空的结点 nextnode=nextnode->left; return nextnode; //返回左下方的结点 } } ThreadBinTree *BinTreePrevious_LDR(ThreadBinTree *bt) //求指定结点的前驱 { ThreadBinTree *prenode; if(!bt) return NULL; //若当前结点为空,则返回空 if(bt->lflag==Thread) //若当前结点的左子树为空 return bt->left; //返回左线索所指的中序后继 else{ prenode=bt->left; //从当前结点的左子树开始查找 while(prenode->rflag==SubTree) //循环处理所有右子树不为空的结点 prenode=prenode->left; return prenode; //返回左下方的结点 } } void ThreadBinTree_LDR(ThreadBinTree *bt,void (*oper)(ThreadBinTree *p)) //遍历中序线索二叉树 { if(bt) //二叉树不为空 { while(bt->lflag==SubTree)//有左子树 bt=bt->left; //从根往下找最左下结点,即中序序列的开始结点 do{ oper(bt); //处理结点 bt=BinTreeNext_LDR(bt);//找中序后继结点 }while(bt); } }
赫夫曼树:最优二叉树(权值最小的)
给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
创建赫夫曼树
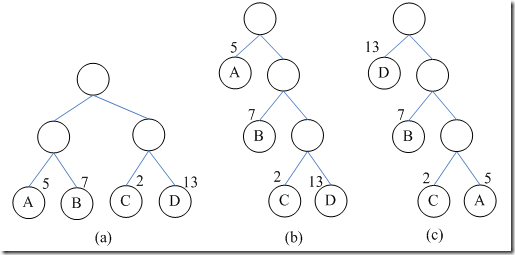
计算下它们各自的权值:
(a) WPL=5×2+7×2+2×2+13×2=54
(b) WPL=5×1+7×2+2×3+13×3=64
(c) WPL=1×13+2×7+3×2+5×3=48
假设有N个权值,则构造出的哈夫曼树有N个叶子结点。 N个权值分别设为 M1、M2、…、MN,则哈夫曼树的构造规则为:
(1) 将M1、M2、…,MN看成是有N棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
若以上图为例:2和5最小,组成一颗,他们的父节点权值为两者之和,也就是7,从余下中寻找最小的,也就是7,他俩在组合…
创建与方法:
#include <stdlib.h> #include <stdio.h> #include <string.h> typedef struct { int weight; //权值 int parent; //父结点序号 int left; //左子树序号 int right; //右子树序号 }HuffmanTree; typedef char *HuffmanCode; //Huffman编码 void SelectNode(HuffmanTree *ht,int n,int *bt1,int *bt2) //从1~x个结点选择parent结点为0,权重最小的两个结点 { int i; HuffmanTree *ht1,*ht2,*t; ht1=ht2=NULL; //初始化两个结点为空 for(i=1;i<=n;++i) //循环处理1~n个结点(包括叶结点和非叶结点) { if(!ht[i].parent) //父结点为空(结点的parent=0) { if(ht1==NULL) //结点指针1为空 { ht1=ht+i; //指向第i个结点 continue; //继续循环 } if(ht2==NULL) //结点指针2为空 { ht2=ht+i; //指向第i个结点 if(ht1->weight>ht2->weight) //比较两个结点的权重,使ht1指向的结点权重小 { t=ht2; ht2=ht1; ht1=t; } continue; //继续循环 } if(ht1 && ht2) //若ht1、ht2两个指针都有效 { if(ht[i].weight<=ht1->weight) //第i个结点权重小于ht1指向的结点 { ht2=ht1; //ht2保存ht1,因为这时ht1指向的结点成为第2小的 ht1=ht+i; //ht1指向第i个结点 }else if(ht[i].weight<ht2->weight){ //若第i个结点权重小于ht2指向的结点 ht2=ht+i; //ht2指向第i个结点 } } } } if(ht1>ht2){ //增加比较,使二叉树左侧为叶结点 *bt2=ht1-ht; *bt1=ht2-ht; }else{ *bt1=ht1-ht; *bt2=ht2-ht; } } void CreateTree(HuffmanTree *ht,int n,int *w) { int i,m=2*n-1;//总的节点数 int bt1,bt2; //二叉树结点序与 if(n<=1) return ; //只有一个结点,无法创建 for(i=1;i<=n;++i) //初始化叶结点 { ht[i].weight=w[i-1]; ht[i].parent=0; ht[i].left=0; ht[i].right=0; } for(;i<=m;++i)//初始化后续结点 { ht[i].weight=0; ht[i].parent=0; ht[i].left=0; ht[i].right=0; } for(i=n+1;i<=m;++i) //逐个计算非叶结点,创建Huffman树 { SelectNode(ht,i-1,&bt1,&bt2); //从1~i-1个结点选择parent结点为0,权重最小的两个结点 ht[bt1].parent=i; ht[bt2].parent=i; ht[i].left=bt1; ht[i].right=bt2; ht[i].weight=ht[bt1].weight+ht[bt2].weight; } } void HuffmanCoding(HuffmanTree *ht,int n,HuffmanCode *hc)//,char *letters) { char *cd; int start,i; int current,parent; cd=(char*)malloc(sizeof(char)*n);//用来临时存放一个字符的编码结果 cd[n-1]='\0'; //设置字符串结束标志 for(i=1;i<=n;i++) { start=n-1; current=i; parent=ht[current].parent;//获取当前结点的父结点 while(parent) //父结点不为空 { if(current==ht[parent].left)//若该结点是父结点的左子树 cd[--start]='0'; //编码为0 else //若结点是父结点的右子树 cd[--start]='1'; //编码为1 current=parent; //设置当前结点指向父结点 parent=ht[parent].parent; //获取当前结点的父结点序号 } hc[i-1]=(char*)malloc(sizeof(char)*(n-start));//分配保存编码的内存 strcpy(hc[i-1],&cd[start]); //复制生成的编码 } free(cd); //释放编码占用的内存 } void Encode(HuffmanCode *hc,char *alphabet,char *str,char *code) //将一个字符串转换为Huffman编码 //hc为Huffman编码表 ,alphabet为对应的字母表,str为需要转换的字符串,code返回转换的结果 { int len=0,i=0,j; code[0]='\0'; while(str[i]) { j=0; while(alphabet[j]!=str[i]) j++; strcpy(code+len,hc[j]); //将对应字母的Huffman编码复制到code指定位置 len=len+strlen(hc[j]); //累加字符串长度 i++; } code[len]='\0'; } void Decode(HuffmanTree *ht,int m,char *code,char *alphabet,char *decode) //将一个Huffman编码组成的字符串转换为明文字符串 //ht为Huffman二叉树,m为字符数量,alphabet为对应的字母表,str为需要转换的字符串,decode返回转换的结果 { int position=0,i,j=0; m=2*m-1; while(code[position]) //字符串未结束 { for(i=m;ht[i].left && ht[i].right; position++) //在Huffman树中查找左右子树为空 ,以构造一个Huffman编码 { if(code[position]=='0') //编码位为0 i=ht[i].left; //处理左子树 else //编译位为 1 i=ht[i].right; //处理右子树 } decode[j]=alphabet[i-1]; //得到一个字母 j++;//处理下一字符 } decode[j]='\0'; //字符串结尾 }
应用:赫夫曼编
int main() { int i,n=4,m; char test[]="DBDBDABDCDADBDADBDADACDBDBD";//对它加密 char code[100],code1[100]; char alphabet[]={'A','B','C','D'}; //4个字符 int w[]={5,7,2,13} ;//4个字符的权重 HuffmanTree *ht; HuffmanCode *hc; m=2*n-1; ht=(HuffmanTree *)malloc((m+1)*sizeof(HuffmanTree)); //申请内存,保存赫夫曼树 if(!ht) { printf("内存分配失败!\n"); exit(0); } hc=(HuffmanCode *)malloc(n*sizeof(char*)); if(!hc) { printf("内存分配失败!\n"); exit(0); } CreateTree(ht,n,w); //创建赫夫曼树 HuffmanCoding(ht,n,hc); //根据赫夫曼树生成赫夫曼编码 for(i=1;i<=n;i++) //循环输出赫夫曼编码 printf("字母:%c,权重:%d,编码为 %s\n",alphabet[i-1],ht[i].weight,hc[i-1]); Encode(hc,alphabet,test,code); //根据赫夫曼编码生成编码字符串 printf("\n字符串:\n%s\n转换后为:\n%s\n",test,code); Decode(ht,n,code,alphabet,code1); //根据编码字符串生成解码后的字符串 printf("\n编码:\n%s\n转换后为:\n%s\n",code,code1); getch(); return 0; }
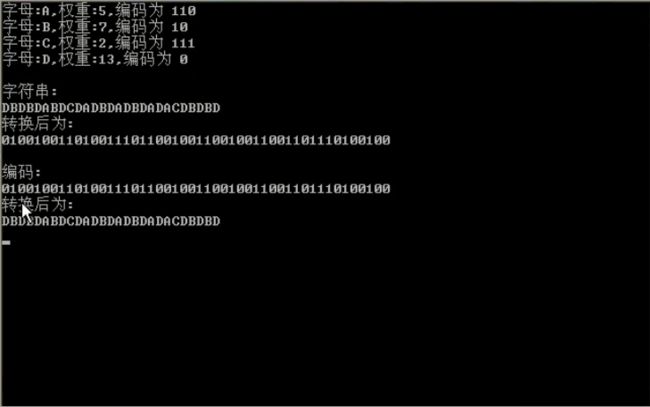
结果:
图解事例: