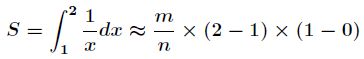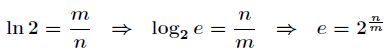蒙特卡洛算法

从今天开始要研究Sampling Methods，主要是MCMC算法。本文是开篇文章，先来了解蒙特卡洛算法。

 文章转载自:http://blog.csdn.net/acdreamers/article/details/44978591

 

Contents

 

   1. 蒙特卡洛介绍

   2. 蒙特卡洛的应用

   3. 蒙特卡洛积分

 

 

 

1. 蒙特卡洛介绍

 

   蒙特卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的

   发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使

   用随机数（或伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特卡罗方法在金融工程

   学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。

 

   蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆

   和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法，

   为它蒙上了一层神秘色彩。在这之前，蒙特卡罗方法就已经存在。1777年，法国数学家布丰提出用投针实验

   的方法求圆周率，这被认为是蒙特卡罗方法的起源。

 

   另外，拟蒙特卡洛算法在近几年也获得迅速发展。这种方法是用确定性的超均匀分布代替蒙特卡洛算法中的

   随机数序列，对于某些特定问题计算速度比普通的蒙特卡洛算法高几百倍。

 

   由于产生随机数的随机性，当我们用N个随机点以蒙特卡罗方法来求解具体的问题时，其计算得到近似解的误

   差值有大有小，但是肯定有一个确定的平均值，即一些误差大于此值，而其余误差小于此值。鉴于此，显然肯

   定存在这样的N个点，使得误差的绝对值不大于平均值。如果我们能够构造这样的点集，就可以对原有的方法

   进行较大的改进。拟蒙特卡罗方法就是至于此而提出的，它致力于构造其误差比平均误差显著要好的那种点集，

   而其求解形式与蒙特卡罗方法一致，只不过所用的随机数不一样。用蒙特卡罗方法求解问题时，影响结果好坏

   的主要是随机数序列的均匀性。而拟蒙特卡罗方法中的具有低偏差的一致分布点集较伪随机数序列更为均匀，

   而且用拟蒙特卡罗方法求解得到的是真正的误差，避免了蒙特卡罗方法得到概率误差的缺陷。

   由此可见用拟蒙特卡罗方法求解问题的关键是如何找到一个均匀散布的点集。目前常用的点集有GLP点集(好格

   子点集，good lattice point set)、GP点集(好点集，good point set)、Halton点集及其变体、

   Hammersley点集等。

 

   蒙特卡洛方法的理论基础是大数定律。大数定律是描述相当多次数重复试验的结果的定律，根据这个定律知道

   样本数量越多，其平均就越趋近于真实值。

 

 

 

2. 蒙特卡洛的应用

 

   最经典的应用就是利用蒙特卡洛算法求圆周率。代码如下

 

代码：

 #include <bits/stdc++.h>

 #define MAX_ITERS 1000000

 using namespace std;

 double Rand(double L, double R)
 {
     return L + (R - L) * rand() * 1.0 / RAND_MAX;
 }

 double GetPi()
 {
     srand(time(NULL));
     int cnt = 0;
     for(int i = 0; i < MAX_ITERS; i++)
     {
         double x = Rand(-1, 1);
         double y = Rand(-1, 1);
         if(x * x + y * y <= 1)
             cnt++;
     }
     return cnt * 4.0 / MAX_ITERS;
 }

 int main()
 {
     for(int i = 0; i < 10; i++)
         cout << GetPi() << endl;
     return 0;
 }

 

3. 蒙特卡洛积分

 

   关于蒙特卡洛求积分，可以先参照如下文章。

 

   链接：http://cos.name/2010/03/monte-carlo-method-to-compute-integration/ 

 

   接下来用蒙特卡洛积分求自然常数。这是2015年阿里的一道笔试题。

 

   首先考虑如下积分

 

       

 

   接下来分别用蒙特卡洛积分和牛顿莱布尼兹公式计算，在蒙特卡洛方法中样本很多时，它们的值应该相等。

 

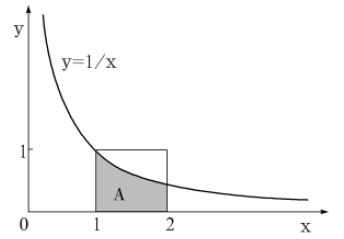
   利用蒙特卡洛方法，图像大致如下

 

       

 

    上述积分的目的是求阴影部分的面积，所以先在所标矩形内取对随机点，

    对于每一对，考察是否满足如下条件

 

         

 

    假设满足上述条件的点有个，而全部的点有个，所以得到近似公式为

 

         

 

    而依据牛顿莱布尼兹公式可以得到

 

          

 

    这两种方法结果应该是相等的，即有

 

          

 

    接下来写写代码吧！

 

代码：

 #include <bits/stdc++.h>

 #define MAX_ITERS 10000000

 using namespace std;

 struct Point
 {
     double x, y;
 };

 double Rand(double L, double R)
 {
     return L + (R - L) * rand() * 1.0 / RAND_MAX;
 }

 Point getPoint()
 {
     Point t;
     t.x = Rand(1.0, 2.0);
     t.y = Rand(0.0, 1.0);
     return t;
 }

 double getResult()
 {
     int m = 0;
     int n = MAX_ITERS;
     srand(time(NULL));
     for(int i = 0; i < n; i++)
     {
         Point t = getPoint();
         double res = t.x * t.y;
         if(res <= 1.0)
             m++;
     }
     return pow(2.0, 1.0 * n / m);
 }

 int main()
 {
     for(int i = 0; i < 20; i++)
         cout << fixed << setprecision(6) << getResult() << endl;
     return 0;
 }

 

    观察一下运行结果，效果还是不错的。如下图