压缩感知KL1p库CompressedSensingExample例子解读

KL1P库是个可以求稀疏表示的库，比如说要求 y=w∗x ,用x来表示y，求系数w，
一般来说思路是最小化 ||y−wx|| ，这个用梯度下降之类的方法就可以求解。
但是如果希望w是稀疏的，比如w是100维，其中只有10维是不为0，其余90维都及其接近于0，那我们就需要添加稀疏性条件，autoencoder和sparse autoencoder便是类似的关系。
KL1P库地址
关于这个库的使用资料不算多，所以从它提供的例子入手是比较好的。

配置方法

下面这篇文章讲得很详细
http://blog.csdn.net/u013088062/article/details/44566667
不过我遇到了点问题，具体如下：
1> 正在生成代码…
1>C:\Program Files\MSBuild\Microsoft.Cpp\v4.0\V110\Microsoft.CppBuild.targets(1299,5): warning MSB8012: TargetPath(E:\cSparse\KL1p-0.4.2\build\win\Debug\KLab.lib) does not match the Library’s OutputFile property value (E:\cSparse\KL1p-0.4.2\bin\win\KLab_d.lib). This may cause your project to build incorrectly. To correct this, please make sure that (OutDir), (TargetName) and (TargetExt)propertyvaluesmatchthevaluespecifiedin1>C:\ProgramFiles\MSBuild\Microsoft.Cpp\v4.0\V110\Microsoft.CppBuild.targets(1301,5):warningMSB8012:TargetName(KLab)doesnotmatchtheLibrary′sOutputFilepropertyvalue(KLabd).Thismaycauseyourprojecttobuildincorrectly.Tocorrectthis,pleasemakesurethat (OutDir), (TargetName)and (TargetExt) property values match the value specified in %(Lib.OutputFile).
1> KLab.vcxproj -> E:\cSparse\KL1p-0.4.2\build\win\Debug\KLab.lib

关于这个问题的描述可以参考
http://www.spirithy.com/vs2012-waring-msb8012.html
解决方法如下，进入该项目的项目属性设置（右击项目名字KLab然后选择属性）：

1、“配置属性”-》“常规”，“输出目录”和“中间目录”都改为：$(SolutionDir)$(Configuration)\

2、“配置属性”-》“链接器”-》“常规”，“输出文件”改为：$(SolutionDir)$(Configuration)\$(TargetName)$(TargetExt)

不过我在vs2012工程里边没有看到链接器这个选项了，变成了库管理器。
Deubg和Release两个模式下都要配置一次。

按照上面说的做过之后，会在debug目录和release目录下边都生成一个KLab.lib文件（类型为Object File Library，我还是第一次用win8，有些不熟悉它这种文件类型表示）。


在debug目录下的要改名字位KLab_d哦！

例子演示

这次采用单步调试的方式一步步来看看它是怎么运行的吧。
文件位于库的example文件夹里边。
写个main函数然后运行runExample例子。

int main()
{
    kl1p::RunExample();
    waitKey(0);
    return 0;
}

如下，在RunExample里边设个断点，开始调试啦。

首先来介绍下几个变量的意义。
首先是m和n，样本数是n，每个样本的特征维数是m。
rho则是稀疏系数，也就是系数x里边不为0的维数的比例。

变量x0

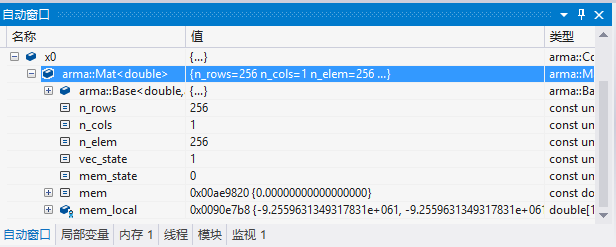
它是个256维的向量，如果想要查看它的具体值，可以打开
调试-》窗口-》内存
这样就可以在内存窗口里边输入内存地址查看值了。
右键点击窗口可以选择数据类型，这里是double，也就是64位浮点数。
我这里每行显示两个数，每个数8个字节，从地址也是可以看出来的。
从图中可以看到x0是很稀疏的。

变量A

接着生成变量A，是一个m*n维的矩阵。
设置均值为0，偏差deviation为1。

        // Create random gaussian i.i.d matrix A of size (m,n).
        klab::TSmartPointer<kl1p::TOperator<klab::DoubleReal> > A = new kl1p::TNormalRandomMatrixOperator<klab::DoubleReal>(m, n, 0.0, 1.0);
        A  = new kl1p::TScalingOperator<klab::DoubleReal>(A, 1.0/klab::Sqrt(klab::DoubleReal(m)));  // Pseudo-normalization of the matrix (required for AMP and EMBP solvers). 

        // Perform cs-measurements of size m.
        arma::Col<klab::DoubleReal> y;
        A->apply(x0, y);

这里的偏差是什么意思啊？
来看看TNormalRandomMatrixOperator里边是怎么定义的吧。
从下面的代码中可以看出，矩阵中每个值的生成都是相互独立的，所以说A是i.i.d.矩阵，也就是indenpendent identically distributed独立同分布。

template<class T>
inline TNormalRandomMatrixOperator<T>::TNormalRandomMatrixOperator(klab::UInt32 m, klab::UInt32 n, const T& mean, const T& deviation, bool normalize) : TMatrixOperator<T>(),
_mean(mean), _deviation(deviation)
{
    arma::Mat<T>& mat = this->matrixReference();

    mat.set_size(m, n);
    for(klab::UInt32 i=0; i<m; ++i)
    {
        for(klab::UInt32 j=0; j<n; ++j)
            mat(i, j) = TNormalRandomMatrixOperatorSpecialisation<T>::GenerateNormalRandomNumber(klab::KRandom::Instance(), mean, deviation); 
    }

    this->resize(m, n);

    if(normalize)
        this->normalize();
}

每个值的生成可以简单看作是
mean + deviation*某个0~1的随机值。
接着A矩阵经历了一次正规化操作，
A = new kl1p::TScalingOperator(A, 1.0/klab::Sqrt(klab::DoubleReal(m))); // Pseudo-normalization of the matrix (required for AMP and EMBP solvers).
这一句过后我调试发现A里边没有矩阵结构，找不着矩阵的mem，也就看不到变化之后的过程了。
所以我做了如下修改：

arma::Mat<klab::DoubleReal> matBeforeNorm(m, n);
        A->toMatrix(matBeforeNorm);
        A  = new kl1p::TScalingOperator<klab::DoubleReal>(A, 1.0/klab::Sqrt(klab::DoubleReal(m)));  // Pseudo-normalization of the matrix (required for AMP and EMBP solvers).      
        arma::Mat<klab::DoubleReal> matAfterNorm(m, n);
        A->toMatrix(matAfterNorm);
        for (int i = 0; i < 2; i++)
        {
            for (int j = 0; j < 256; j++)
            {
                double d1 = matBeforeNorm.at(i, j);
                double d2 = matAfterNorm.at(i, j);
                std::cout << d2/d1 << " ";
            }
            std::cout << "1.0/klab::Sqrt(klab::DoubleReal(m)):" << 1.0/klab::Sqrt(klab::DoubleReal(m))<<std::endl;
        }

从结果可以看出，正规化操作也就是对A中所有元素都乘以一个1.0/klab::Sqrt(klab::DoubleReal(m))

下面这几句是构造测试样本y了，y是个128维的向量。
不过apply函数我没看明白是干嘛的。
它的作用我会在后边进行猜测并进行实验验证。

        // Perform cs-measurements of size m.
        arma::Col<klab::DoubleReal> y;
        A->apply(x0, y);

BasicPursuit的使用

误差tolerance设置为了1e-3.
bp.solve(y, A, x)这一句里边，
A是字典，1个m*n维的矩阵，m是每个样本的特征维数，n是样本总数，
y是测试样本，1个m维向量，
x则是结果，是一个n维向量，表示用n个样本对y进行表示的结果。

        klab::DoubleReal tolerance = 1e-3;  // Tolerance of the solution.
        arma::Col<klab::DoubleReal> x;      // Will contain the solution of the reconstruction.

        klab::KTimer timer;

        // Compute Basis-Pursuit.
        std::cout<<"[BasisPursuit] Start."<<std::endl;
        timer.start();
        kl1p::TBasisPursuitSolver<klab::DoubleReal> bp(tolerance);
        bp.solve(y, A, x);
        timer.stop();
        std::cout<<"[BasisPursuit] Done - SNR="<<std::setprecision(5)<<klab::SNR(x, x0)<<" - "
        <<"Time="<<klab::UInt32(timer.durationInMilliseconds())<<"ms"<<" - "
        <<"Iterations="<<bp.iterations()<<std::endl;

在最后用x与x0进行比较，所以我猜测y是由x0生成的，恰好x0是个稀疏变量，所以由y得到的x也应该是个稀疏变量。
下面我写段代码来进行验证：
yx0表示由x0生成的样本，yx则表示由x生成的样本。
生成方式：x0的第i个值与matAfterNorm的第i列进行相乘（也就是一个常量*一个向量），yx0则是把这些结果都累加一遍，实质便是matAfterNorm在x0的表示下的结果。
yx生成方式同上。

        arma::Col<klab::DoubleReal> yx0 = arma::zeros(m);
        arma::Col<klab::DoubleReal> yx = arma::zeros(m);
        int count_x0 = 0;
        int count_x = 0;
        for (int i = 0; i < n; i++)
        {
            yx0 = yx0 + matAfterNorm.col(i)*x0(i);
            yx = yx + matAfterNorm.col(i)*x(i);
            if (x0(i) > 1e-6)
                count_x0++;
            if (x(i) > 1e-6)
                count_x++;
        }
        double d1 = klab::SquaredError(yx, y);
        double d2 = klab::SquaredError(yx0, y);
        double d3 = klab::SquaredError(yx0, yx);

从结果看出，d2几乎为0，这也证明y确实是由x0以及A生成的。
稀疏系数x得到的结果与y的差距也不大，证明结果精度也不错哦！

至于稀疏情况，count_x的值是26，count_x0的值则是11，说明在稀疏情况下x还是没有最初的x0效果那么好。

换个输入看看效果

我使用A中第一列作为测试样本，看看效果如何

arma::Col<klab::DoubleReal> y = matAfterNorm.col(0);

x结果如下，只有第一个是大于1e-6,其余都是小于1e-6的哦，实验很完美，运行378ms。

arma::Col<klab::DoubleReal> y = matAfterNorm.col(0)*0.3 + matAfterNorm.col(1)*0.4;

结果依然很好，运行426ms。

这次换个比较奇葩的输入，y全为1。

arma::Col<klab::DoubleReal> y = arma::zeros(m);
y = y+1;

结果就乱七八糟了，x中大于1e-6的值有116个，而且时间也花了14418ms，说明这个输入用A进行表示结果很不好哦！