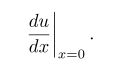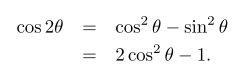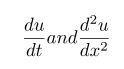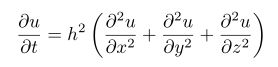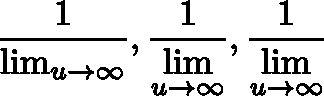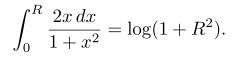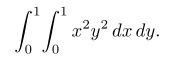LaTeX数学公式

LaTeX数学公式 

1、数学公式的前后要加上 $ 或 \( 和 \)，比如：$f(x) = 3x + 7$ 和 \(f(x) = 3x + 7\) 效果是一样的；
如果用 \[ 和 \]，或者使用 $$ 和 $$，则该公式独占一行；
如果用 \begin{equation} 和 \end{equation}，则公式除了独占一行还会自动被添加序号， 如何公式不想编号则使用 \begin{equation*} 和\end{equation*}.

2、字符
普通字符在数学公式中含义一样，除了
# $ % & ~ _ ^ \ { }
若要在数学环境中表示这些符号# $ % & _ { }，需要分别表示为\# \$ \% \& \_ \{ \}，即在个字符前加上\。

3、上标和下标
用 ^ 来表示上标，用 _ 来表示下标，看一简单例子：

$$\sum_{i=1}^n a_i=0$$
$$f(x)=x^{x^x}$$

效果:

这里有更多的LaTeX上标下标的设置

4、希腊字母

正体希腊字母
特征	语法	效果	注释/外部链接
大写字母	\Alpha \Beta \Gamma \Delta \Epsilon \Zeta \Eta \Theta		Α  Β  Γ  Δ  Ε  Ζ  Η  Θ
	\Iota \Kappa \Lambda \Mu \Nu \Xi \Omicron \Pi		Ι  Κ  Λ  Μ  Ν  Ξ  Ο  Π
	\Rho \Sigma \Tau \Upsilon \Phi \Chi \Psi \Omega		Ρ  Σ  Τ  Υ  Φ  Χ  Ψ  Ω
小写字母	\alpha \beta \gamma \delta \epsilon \zeta \eta \theta
	\iota \kappa\varkappa \lambda \mu \nu \xi \omicron \pi
	\rho \sigma \tau \upsilon \phi \chi \psi \omega
异体字母	\Epsilon\epsilon\varepsilon
	\Theta\theta\vartheta
	\Kappa\kappa\varkappa
	\Pi\pi\varpi
	\Rho\rho\varrho
	\Sigma\sigma\varsigma
	\Phi\phi\varphi
已停用字母	\digamma		Ϝ [1]

5、数学函数

例如sin x， 输入应该为\sin x

6、在公式中插入文本可以通过 \mbox{text} 在公式中添加text，比如：

\documentclass{article}
\usepackage{CJK}
\begin{CJK*}{GBK}{song}
\begin{document}
$$\mbox{对任意的$x>0$}, \mbox{有 }f(x)>0. $$
\end{CJK*}
\end{document}

效果:

7、分数及开方
\frac{numerator}{denominator} \sqrt{expression_r_r_r}表示开平方，
\sqrt[n]{expression_r_r_r} 表示开 n 次方.

8、省略号（3个点）
\ldots 表示跟文本底线对齐的省略号；\cdots 表示跟文本中线对齐的省略号，

比如：

表示为 $$f(x_1,x_x,\ldots,x_n) = x_1^2 + x_2^2 + \cdots + x_n^2 $$

9、括号和分隔符
() 和 [ ] 和 ｜ 对应于自己；
{} 对应于 \{ \}；
|| 对应于 \|。
当要显示大号的括号或分隔符时，要对应用 \left 和 \right，如：

\[f(x,y,z) = 3y^2 z \left( 3 + \frac{7x+5}{1 + y^2} \right).\]对应于

\left. 和 \right. 只用与匹配，本身是不显示的，比如，要输出：

则用 $$\left. \frac{du}{dx} \right|_{x=0}.$$

10、多行的数学公式

可以表示为：

\begin{eqnarray*}
\cos 2\theta & = & \cos^2 \theta - \sin^2 \theta \\
& = & 2 \cos^2 \theta - 1.
\end{eqnarray*}

其中&是对其点，表示在此对齐。
*使latex不自动显示序号，如果想让latex自动标上序号，则把*去掉

11、矩阵

表示为：

The \emph{characteristic polynomial} $\chi(\lambda)$ of the
$3 \times 3$~matrix
\[ \left( \begin{array}{ccc}
a & b & c \\
d & e & f \\
g & h & i \end{array} \right)\]
is given by the formula
\[ \chi(\lambda) = \left| \begin{array}{ccc}
\lambda - a & -b & -c \\
-d & \lambda - e & -f \\
-g & -h & \lambda - i \end{array} \right|.\]

c表示向中对齐，l表示向左对齐，r表示向右对齐。

12、导数、极限、求和、积分(Derivatives, Limits, Sums and Integrals)

The expression_r_r_rs

are obtained in LaTeX by typing

\frac{du}{dt} and \frac{d^2 u}{dx^2}

respectively. The mathematical symbol  is produced using \partial. Thus the Heat Equation

is obtained in LaTeX by typing

\[ \frac{\partial u}{\partial t}
= h^2 \left( \frac{\partial^2 u}{\partial x^2}
+ \frac{\partial^2 u}{\partial y^2}
+ \frac{\partial^2 u}{\partial z^2}\right)\]

To obtain mathematical expression_r_r_rs such as

in displayed equations we type \lim_{x \to +\infty}, \inf_{x > s} and\sup_K respectively. Thus to obtain

(in LaTeX) we type

\[ \lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3.\]

Added by Goldman2000@126:-------------------------

To compulsively display "u \to \infty" under the limit, 

 

we type in LaTeX

\frac{1}{\lim_{u \rightarrow \infty}}, \frac{1}{\lim\limits_{u \rightarrow \infty}} or

\frac{1}{ \displaystyle \lim_{u \rightarrow \infty}} respectively.

Ended by Goldman2000@126: -------------------------

To obtain a summation sign such as

we type \sum_{i=1}^{2n}. Thus

is obtained by typing

\[ \sum_{k=1}^n k^2 = \frac{1}{2} n (n+1).\]

We now discuss how to obtain integrals in mathematical documents. A typical integral is the following:

This is typeset using

\[ \int_a^b f(x)\,dx.\]

The integral sign is typeset using the control sequence \int, and the limits of integration (in this case a and b are treated as a subscript and a superscript on the integral sign.
Most integrals occurring in mathematical documents begin with an integral sign and contain one or more instances of d followed by another (Latin or Greek) letter, as in dx, dy and dt. To obtain the correct appearance one should put extra space before the d, using \,. Thus

and

are obtained by typing

\[ \int_0^{+\infty} x^n e^{-x} \,dx = n!.\]

\[ \int \cos \theta \,d\theta = \sin \theta.\]

\[ \int_{x^2 + y^2 \leq R^2} f(x,y)\,dx\,dy
= \int_{\theta=0}^{2\pi} \int_{r=0}^R
f(r\cos\theta,r\sin\theta) r\,dr\,d\theta.\]

and

\[ \int_0^R \frac{2x\,dx}{1+x^2} = \log(1+R^2).\]

respectively.

In some multiple integrals (i.e., integrals containing more than one integral sign) one finds that LaTeX puts too much space between the integral signs. The way to improve the appearance of of the integral is to use the control sequence \! to remove a thin strip of unwanted space. Thus, for example, the multiple integral

is obtained by typing

\[ \int_0^1 \! \int_0^1 x^2 y^2\,dx\,dy.\]

Had we typed

\[ \int_0^1 \int_0^1 x^2 y^2\,dx\,dy.\]

we would have obtained

A particularly noteworthy example comes when we are typesetting a multiple integral such as

Here we use \! three times to obtain suitable spacing between the integral signs. We typeset this integral using

\[ \int \!\!\! \int_D f(x,y)\,dx\,dy.\]

Had we typed

\[ \int \int_D f(x,y)\,dx\,dy.\]

we would have obtained

The following (reasonably complicated) passage exhibits a number of the features which we have been discussing:

One would typeset this in LaTeX by typing In non-relativistic wave mechanics, the wave function
$\psi(\mathbf{r},t)$ of a particle satisfies the
\emph{Schr\"{o}dinger Wave Equation}
\[ i\hbar\frac{\partial \psi}{\partial t}
= \frac{-\hbar^2}{2m} \left(
\frac{\partial^2}{\partial x^2}
+ \frac{\partial^2}{\partial y^2}
+ \frac{\partial^2}{\partial z^2}
\right) \psi + V \psi.\]
It is customary to normalize the wave equation by
demanding that
\[ \int \!\!\! \int \!\!\! \int_{\textbf{R}^3}
\left| \psi(\mathbf{r},0) \right|^2\,dx\,dy\,dz = 1.\]
A simple calculation using the Schr\"{o}dinger wave
equation shows that
\[ \frac{d}{dt} \int \!\!\! \int \!\!\! \int_{\textbf{R}^3}
\left| \psi(\mathbf{r},t) \right|^2\,dx\,dy\,dz = 0,\]
and hence
\[ \int \!\!\! \int \!\!\! \int_{\textbf{R}^3}
\left| \psi(\mathbf{r},t) \right|^2\,dx\,dy\,dz = 1\]
for all times~$t$. If we normalize the wave function in this
way then, for any (measurable) subset~$V$ of $\textbf{R}^3$
and time~$t$,
\[ \int \!\!\! \int \!\!\! \int_V

\left| \psi(\mathbf{r},t) \right|^2\,dx\,dy\,dz\]
represents the probability that the particle is to be found
within the region~$V$ at time~$t$.

上标、下标及积分等

功能	语法	效果
上标	a^2
下标	a_2
组合	a^{2+2}
	a_{i,j}
结合上下标	x_2^3
前置上下标	{}_1^2\!X_3^4
导数 （HTML）	x'
导数 （PNG）	x^\prime
导数 （错误）	x\prime
导数点	\dot{x}
	\ddot{y}
向量	\vec{c}
	\overleftarrow{a b}
	\overrightarrow{c d}
	\widehat{e f g}
上弧 (注: 正确应该用 \overarc, 但在这里行不通。要用建议的语法作为解决办法)	\overset{\frown} {AB}
上划线	\overline{h i j}
下划线	\underline{k l m}
上括号	\overbrace{1+2+\cdots+100}
	\begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 } \end{matrix}
下括号	\underbrace{a+b+\cdots+z}
	\begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26 \end{matrix}
求和	\sum_{k=1}^N k^2
	\begin{matrix} \sum_{k=1}^N k^2 \end{matrix}
求积	\prod_{i=1}^N x_i
	\begin{matrix} \prod_{i=1}^N x_i \end{matrix}
上积	\coprod_{i=1}^N x_i
	\begin{matrix} \coprod_{i=1}^N x_i \end{matrix}
极限	\lim_{n \to \infty}x_n
	\begin{matrix} \lim_{n \to \infty}x_n \end{matrix}
积分	\int_{-N}^{N} e^x\, dx
	\begin{matrix} \int_{-N}^{N} e^x\, dx \end{matrix}
双重积分	\iint_{D}^{W} \, dx\,dy
三重积分	\iiint_{E}^{V} \, dx\,dy\,dz
四重积分	\iiiint_{F}^{U} \, dx\,dy\,dz\,dt
闭合的曲线、曲面积分	\oint_{C} x^3\, dx + 4y^2\, dy
交集	\bigcap_1^{n} p
并集	\bigcup_1^{k} p

 基本的数学公式编辑

上下标： ， ， ， ， ，	x^n，x^{123}，x_n，x_{123}，C_n^ m，C_{100}^{50}   注意：当上标或下标非单个数字或字母时要加 花括号括起整体，否则只会对首个数字或字母 生效（比如 x^10 会显示 $x^10$），下同
花括号：	\{a_n\}    在各种括号的输入中，只有花括号才需要加反 斜杠，其余直接输入即可。
分式：，，	\frac{a}{b}，\frac12，\frac1{23}
根式：，，，	\sqrt{a}，\sqrt[n]{a}， \sqrt2，\sqrt[3]2
对数：，，	\log_ab，\ln a，\lg10    中间的ln和a之间的空格必不可少。简言之， 若命令后紧跟的是英文字母，就必须用空格 隔开，否则 \lna 这样会被系统理解为一个新 的未知命令而报错，若紧跟数字则可以不空。
和式：	\sum_{k=1}^{n}f(k)
积式：	\prod_{k=1}^{n}f(k)
极限：	\lim_{k\to\infty}k^{-1}=0 与和式类似，此外，\to 是 $\to$，\infty 是 $\infty$
积分：	\int_{a}^{b}f(x)dx 与和式类似。
正负、负正：，，，	\pm1，\mp1，\pm x，\mp x 后面两个记得不要少了的空格。
同余： 不带括号： 带括号：	不带括号：a\equiv b\mod cd 带括号：a\equiv b\pmod{cd} 后者的括号是自动加的，不需要手打，但注意 花括号不要少，除非是单个字符
短的左推出、右推出、等价于：，，	\Rightarrow，\Leftarrow，\Leftrightarr ow，若首字母不大写则变成  ，， 另外，$ 和 也可分别用\to 和\gets 得。
长的左推出、右推出、等价于：，，	\Longrightarrow，\Longleftarrow，\Longleftrightarrow  也有类似的首字母不大写的情况。 另外，还有简写：\iff 得
大小关系：，，，，	\ge，\le，\ne，\equiv，\approx    对于 前两个，后加 qslant 则变成更好看的，
相似（或等价量）、全等：，	\sim，\cong
导数：，，	f'(x)，f''(x)，f'''(x) 注意：撇 ' 由右单引号键打出（台式机键 盘在中括号下面，必须要在纯英文状态下 输入），二阶就打两撇，而不是打双引号， 三阶就三撇，如此类推。
常用希腊字母：  ，，，，，，  ，，，，，  （），（）	\pi，\alpha，\beta，\gamma，\theta， \rho，\lambda，\mu，\Delta，\xi， \omega，\phi（\varphi），\epsilon （\varepsilon）
三角函数、度：，，，	\sin x，\cos^2x，\tan30^\circ， \cot^245^\circ 有些空格能省，有些不能，自己理解。
三角形、圆、角、垂直：，，，	\triangle，\odot，\angle，\perp 注意：不要用(\Delta) 来表示三角形， 判别式才是
点乘、叉乘、除以：，，	a\cdot b，1\times2，355\div113
存在、任意、非、或、且：，，，，	\exists，\forall，\neg（或 \lnot）， \vee（或 \lor），\wedge（或 \land）
补集、空集：，	\complement，\varnothing 空集不推荐用那个 \emptyset（效果：） 更不应该用 \phi（效果：）
并、交、包含、真包含：，，，，，	\cup，\cap，\subseteq，\supseteq， \subsetneqq，\supsetneqq 如果习惯，的就用 \subset，\supset
属于、不属于：，	\in，\notin 另外，还有 \ni 得到
组合数：	{n\choose m} 两边花括号不要少，注意空格。
分段函数：	以前用 \cases，后来发现有点问题，现改 用cases环境： $f(x)=\begin{cases} x+1 & x>0 \\ 1-x & x<0 \end{cases}$
向量：，，，	\hat {a}，\vec a，\overrightarrow{a}，\overrightarrow{AB} 其中\vec 只适用于单个字母的向量
上下括号：	n=\underbrace{1+1+\cdots+1}_{n~个}=\overbrace{1+1+\cdots+1}^{n~个} 那个 ~ 是为了在 $n$ 和“个”字之间隔开 一小距离，此乃中英混排的习惯