(连载)边喝咖啡边学Unity——第二章 预备知识体系

第二章 预备知识体系

——本章涉及空间数学、解析几何、线性代数、计算机图形学、算法、数据结构等众多基础学科。同上一章相比，虽然枯燥，但是绝不能称为废话之章，即使粗略的看一遍，也比直接跳过来的好，详细地读完，会让读者以后的开发之路走的更加平坦。

并且本章的知识不仅仅对您的Unity游戏开发有帮助，对于大部分软件开发人员都是大有作用的。

作为传统3D游戏编程来讲，需要运用到的知识面非常之广，涉及到的学科特别之多。而通常讲编程的书籍，会弱化数学知识，讲数学的书籍，会弱化编程方面的知识。这就是我在第一章所提到的数学与编程之间的空白。而连接着数学与3D游戏编程之间的纽带我们简单地叫他空间数学。尽管Unity已经封装了底层图形接口，无需我们具体编写即可完成游戏开发，但是对显卡、GPU编程、计算机图形学一窍不通的人写出来的程序很难说不会有这样那样的问题，不管是从性能上还是从兼容性方面。更何况我们学习Unity编程之初就立马会遇到向量乘法，欧拉角。如果没有相关知识做铺垫，很难理解那些代码到底在做什么。试想一下我们在设定一个角色的欧拉角的时候，你大呼一声，不就是欧拉角么！我们图论里面不就学过了欧拉图(所有边一次且仅一次行遍图中所有顶点的通路称为欧拉通路，通过图中所有边一次且仅一次行遍所有顶点的回路称为欧拉回路。具有欧拉回路的图称为欧拉图。)，肯定跟那个有关系的一个东西而已啦。那就错了！欧拉角跟欧拉图是八竿子打不着的两个东西。

        坦白讲，我对数学是又爱又恨。爱数学因为很多时候数学知识让我们验证了不少问题。恨数学因为单纯的数学太晦涩深奥。回想我的学习生涯，英语和理化一直是我的拿手菜，数学成绩却从一开始就作着正弦曲线一般的波动。工作之后，越发意识到数学的重要性，现在的各行各业所需要的基础专业学科都可以说是自然科学的分支，而自然科学从一开始就抱死了数学的大腿，没有数学支持，任何自然科学都不复存在。所以请调整好心态跟随笔者学习本章的基础知识，遇到数学知识淡淡地一笑，无法理解就简单地比划比划吧。

        与Unity开发紧密相连的学科

计算机图形学、线性代数、立体几何、数据结构这些是明显有联系的学科，当然更进阶一点，网络编程、计算机组成原理、数据库等也是不可或缺。读者要明白一点，本章不可能把如此多的学科一下子塞到一章里面，只能是挑重要的内容来讲，其中的每一个学科都可能是大学里面一年的课程，对于一笔带过的知识点，希望读者有着强烈的愿望查阅相关资料来学习。

计算机图形学部分

概念:计算机图形学一门主要研究用计算机及其图形设备来输入、表示、变换、运算和输出图形的原理、算法及系统的学科。在游戏开发中我们更关心如何来输出接近真实的图形图像。

在计算机中，图形一般有两大类，位图(由像素点组成)与矢量图(由矢量组成)。前者的特性有:占用空间大、压缩不可逆、放大会失真但是由于已经是一个个的像素颜色了，因此计算机不需要特别的处理就可以用显示器来表达。后者则体积小，可随意缩放，但是最终显示到屏幕上仍需要转换。

接下来显示器又如何将图形变成光信号让我们的视网膜所看见呢？主流显示器的发展大致可以分为3大块：

阴极射线管显示器(CRT——Cathode Ray Tube)，这种显示器90后以前的人肯定都知道，物理教科书中也有详细的描述，带负电荷的射线经过一个可调节场强的磁场发生偏转后打到屏幕上的不同位置，产生图像。

液晶显示器(LCD——Liquid Crystal Display)，应该是目前基本上所有读者都在使用的显示器了吧，液晶显非常的薄，我们的移动设备也是得益于液晶显示器才可以超薄。它的主要原理是以电流刺激液晶分子产生点、线、面配合背部灯管构成画面。

等离子显示器(PDP——Plasma Display Panel)，是采用了近几年来高速发展的等离子平面屏幕技术的最新一代显示设备。成像原理是在显示屏上排列上千个密封的小低压气体室，通过电流激发使其发出肉眼看不见的紫外光，然后紫外光碰击后面玻璃上的红、绿、蓝3色荧光体发出肉眼能看到的可见光，以此成像。

计算机图形处理器

图形处理器(GPU——Graphics Processing Unit)，它是连接显示器和个人电脑主板的重要元件，将计算机系统所需要的显示信息进行转换驱动，并向显示器提供行扫描信号，控制显示器的正确显示。它的英文缩写跟我们的中央处理器CPU非常像，只不过GPU是专为执行复杂的数学和几何计算而设计的，这些计算是图形渲染所必需的。更重要的是CPU可以执行各种执行，GPU只负责处理图形指令。它的主要任务是对系统输入的视频信息进行构建和渲染，各图形函数基本上都在这里集成，比如现在许多3D显卡都支持的OpenGL硬件加速，DirectX功能以及各种纹理渲染功能都是在这里实现的。

 

GPU又是构成显卡的核心部件。GPU+显存+RAMDAC=显卡，其中RAMDAC也就是视频存储数字模拟转换器，作用是把二进制数字转换成和显示器相适应的模拟信号。显卡对于大家已经相当熟悉了，显卡的性能还是大家挑选电脑的重要指标。显存是用来存储显示的图形信息以及保存图形运算的中间数据。其大小和速度直接影响GPU性能的发挥。越大越好，越快越好。因此一块好的显卡不光GPU的主频要高，显存的大小也很重要(游戏发烧友配电脑的时候肯定都知道这个)。

 

着色(Shade)与渲染(Render)

着色与渲染看起来功能相似，实则截然不同。着色用以显示出简单的灯光效果、阴影效果和表面纹理效果。渲染则是把模型或者场景输出成图像文件、视频信号的过程。

 

关于计算机图形学的知识本书到这里，而这门庞大的学科还有很多知识需要读者自行学习。

 

线性代数部分

 

向量与标量

第一章已经提到Unity中大部分地方都是用向量来表达属性。那么向量是什么？标量是什么呢？取定单位后可以用一个实数表达的量叫做标量，例如长度、面积、时间等。既有方向又有大小的量叫做向量(也叫矢量)。例如速度、力、位移等。

特殊地，在3D编程中，我们普遍认为点和向量是一个概念，本书中也不会去区分这2个名词。向量有一个特点，即它没有位置的概念。也就是说只要是长度和方向相同的两个向量，即使起点不同，我们也认为是同一个向量。

 

坐标系

坐标系应该是大家很熟悉的东西了。坐标系是用来量化空间的。我简单的讲一讲常见的几种坐标系。我们接触最多的坐标系，应该是平面直角坐标系了，后面讲纹理贴图的时候会提到一个纹理坐标系，其实就是一个特殊的平面直角坐标系。平面直角坐标系有两个约束词语：平面、直角。显然坐标系还可以不在一个平面，也可以不是直角的。

平面直角坐标系我们简单的叫它2维坐标系，因为它有两个坐标轴:x与y。从1维，到2维，到3维，到更高维度的坐标系，用来描述更高维度的空间。其中我们人能够最直接理解的是3维空间，4维以后的空间，需要极高的想象力才能想象，比较抽象，而随着人类的进化能够直接感知和控制更高的维度，也不是不可能的，很多的科幻小说都经常会描述高维度的空间。

从物理学的角度讲，宇宙中的维度多大10几个维度，并且物理学中的维度，与数学中的维度有区别。人是一种低维度的生物，想要认知和理解更高维度的空间，最简单的方式就是投影。比如4维空间中的超正方体，我们人类很难直接理解，可以将以某种方式其投影至3维空间，看到超正方体在3维空间的影子来想象4维空间中超正方体的样子，就好比把人投影到墙上，根据影子来想象这个人的样子一样。为什么是某种方式是，因为投影的角度不同，得到的影子也会不同。

昨天笔者才去电影院看了最近声名大噪的科幻片《星际穿越》，其中描述的黑洞就是一个未来人类打造的一个高维度空间的超正方体。这部片子我挺喜欢的，里面很多细节都引人深思，比如宇航员描述虫洞的时候。以前很多人理解的虫洞都是一个圆形的洞，而这部电影中给出虫洞球体的形象和解释让我更为信服。虫洞是由爱因斯坦和罗森共同发现的相对论方程式中的一个可能的解，其物理意义为引力场可以弯曲时空，以至于本来相聚遥远的两个位置被弯曲后变得很近，使之成为一条连接这2个位置的捷径。宇航员将一张纸弯曲，然后用笔穿过，再展开，说道：”这张纸是一个二维空间，通过更高的维度(3维空间)弯曲这个空间后形成虫洞，再展开这张纸还原成二维空间，我们看到了虫洞从3维空间到2维空间中的投影为一个圆形的洞。那么三维空间中的两个位置经由更高的维度弯曲形成虫洞后投影在3维空间，就应该是一个球体而不是圆！“。如果你看这部电影的时候看懂了他说的这段话，我相信你有不错的空间想象力！可推想4维空间中虫洞就应该是一个超球体，等等。

说道维度的变迁，不得不给大家讲一个我最喜欢讲的故事。加如我是一个二维生物，一辈子生活在一个平面的空间里，我们认为一个正方形是一个非常封闭的形状，因此我们把贵重的物品用一个正方形来存放，并想着”只要我的正方形不被切开，里面的东西怎么可能被人拿走呢？”。直到有一天我来到三维空间，发现我可以直接从正方形的上下方把东西拿走，完全需要理会那个正方形的时候，我感到异常震惊！原来正方形不是那么牢不可破啊！！听完这个故事，我们换一个版本就可以改为我是一个三维生物，我认为正方体是一个非常封闭的形状，比如保险箱，我们用来存放贵重物品，直到有一天我进入了四维空间之后发现我可以直接从一个完全密闭的箱子中拿东西而不需要破坏那个箱子…………其实空间对于人的认知来讲，每多一个维度，不仅仅是多一个坐标轴那么简单，而是带来无限多的可能性和颠覆性。

 

言归正传，我们用n个坐标轴来描述n个维度空间的坐标系，即平面直角坐标系去掉平面(更高维度)和直角(加入斜角)这两个约束词，有一个高大上的名字：笛卡尔坐标系。哈哈，所以当你想让别人觉得你高大上的话，你可以这样说：我们在一个笛卡尔坐标系中给定2个点……笛卡尔的拉丁化名字叫做瑞那图斯·卡提修斯，因此笛卡尔坐标系还有个更高大上的名字：卡提修斯坐标系。

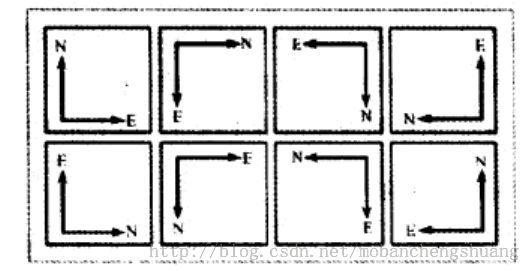
笛卡尔，是一位数学家、哲学家以及各种各样的家，他还是解析几何之父。很早以前我们的自然科学的各个分支并没有那么明确，所以这种描述是经常看到的，牛顿还是一个神学家呢。笛卡尔是如何创建笛卡尔坐标系的呢？有一个虚构的故事讲的是相传很久以前，有个国家要建一座城市——笛卡尔城，设计师设计了一张地图，第一次采用了垂直街道的布局方式，中央的两条街道经过城镇的中心向北与向东。其他的街道也都是这两个走向，地图上的每个位置能根据在东西和南北向的那两条街道旁边来描述。最后设计师将这张设计图交给建筑师来建造的时候，由于上面没有写字，因此建筑师发现不知道应该怎样拿这张设计图来建造这个城才是正确的。最后他们开会讨论，分析出城镇中心在左下角来看这张设计图比较好。这当然只是个传说，实际上，平面直角坐标系的一个象限在一个平面里面可以8种形态：

即坐标的圆点在4个位置，以及两个轴(axis)的位置一共有这8种组合。

这8种情况，上面4种，我们认为是一样的，就是前面故事所讲，只要我们旋转这个地图，不同的方向拿就会得到这4种情况，后面3种都能经过旋转变为第一个。下面这4种实质上也可以变为第一个，其过程是除了旋转之外，还需要将这张纸翻一面，或者说从背面去看这张纸。

也就是说二维直角坐标系总是能通过旋转(纸张翻转可以认为是绕轴旋转，否则按几何中心旋转)得到同一个形式。

但是3维直角坐标却没有这个特点。

 

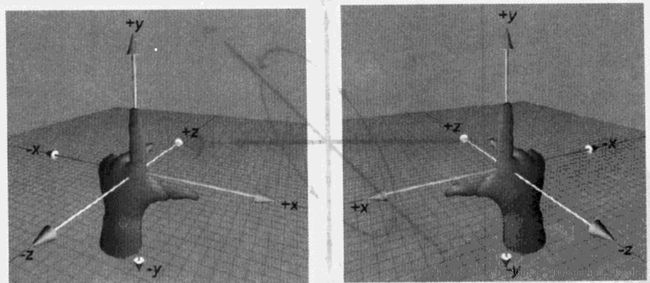
在三维直角坐标系中，由上面这个图，我们分为两种坐标系：左手坐标系与右手坐标系，即伸出我们的左手和右手，将大拇指、食指、中指两两垂直，然后分别按照大、食、中的顺序对应x、y、z轴的正方向，得到左右手坐标系。我们发现我们无论如何也无法通过旋转这3个手指让左手坐标系变为右手坐标系。(PS:其实我们能够通过旋转将二维坐标系归一，借助了第三个维度，翻转的时候是在三维空间中翻转，改变朝向的时候是沿着z轴在旋转。因此前面讲的故事可想认知由于我们人类的认知有限，对于4维以上的空间非常难理解，因此左手坐标系与右手坐标系到更高维度后是不是也可以借助第4个维度的轴进行旋转来归一呢？)

在理解了左手坐标系和右手坐标系之后，鉴于目前人类的认知，我们在使用的时候必须区分开来，不同类型的3维坐标系要分清楚。Unity中采用的坐标系是左手坐标系，而3DMax等建模工具中使用的坐标系是右手坐标系，必要的时候需要进行换算。

同时，左手坐标系和右手坐标系中，我们的一些法则也需要使用不同的手来确定，比如向量叉乘后的方向、旋转向量的方向都需要使用对应的手来比划。具体的左右手法则本章后面会详细提及。

 

常用的坐标系除了笛卡尔坐标系之外，还有极坐标系。极坐标系是由极点、极轴和极径组成的坐标系。极坐标系用来描述曲线和曲面非常给力。我们只需要了解一下即可。地球用极坐标系来描述就比用直角坐标系来描述方面的多。极坐标中的正弦曲线非常美丽，是一个玫瑰线。还有一些方程只能在极坐标系中描述，图案也很漂亮。

笛卡尔还有一个传说，说的是他晚年的时候是公主克里斯汀的老师，这两位师生上演了一段惊世骇俗的爱情，被国王知道后，国王震怒。于是国王下令将笛卡尔驱逐。笛卡尔被驱逐之后，两个非常的思念彼此，于是笛卡尔经常给克里斯汀写信诉相思，克里斯汀看完后也给笛卡尔回信。然后可恶的国王又发现了此时，于是将笛卡尔的来信全部拦截，克里斯汀长期收不到笛卡尔的信，以为笛卡尔不爱他了，日渐消瘦。而笛卡尔也身心憔悴最后患上恶疾。在笛卡尔行将就木的时候，还是忍不住相思情给克里斯汀写下最后一封信就去世了，信的内容竟然简短的只有一行数学方程式。这封当时世界上基本上没有人能看懂的情书，国王看到之后也不明所以，看到克里斯汀面容憔悴便想反正就一行数学方程式，变把这封信交给克里斯汀希望她能好过一点。克里斯汀拆开信之后泪如泉涌，知道笛卡尔一直还爱着他，这封最短的情书当时全世界就他们师生二人能够看懂，那个数学方程式就是：r=a(1－sinθ)。

这个方程式的图像只能在极坐标系中表示，其图像是一个爱心。

读者们，还等什么呢？表白的时候是不是又有新技能Get？

 

 

 

向量的运算

为何把向量的运算放在坐标系后面来讲呢，因为前面讲了投影这个方法，而向量的运算里面经常需要投影。

向量的相等：两个向量的大小和方向都相等。

向量求模：对于一个向量u,我们只取它的大小，无视其方向，就叫求模。用符号来表示u的模。由于向量没有位置的概念，因此我们可以认为任何n维向量都可以是起点在平面坐标系的圆点上的，因此对于任意向量我们可以由终点的坐标来表示。所以说本书约定点和向量的概念不予区分。对于一个3维向量，终点为p(x,y,z),我们根据勾股定理可以轻松算得其模。

向量的投影：对于一个向量u,将其投影至另一个向量v，夹角为theta，我们演u的终点做一条垂线交于v，同样由勾股定理得知u在v的投影大小为，方向为<90°且>240°与v同向，>90°且<240°时与v反向

 

特殊的，一个向量u由终点p(x,y,z)表示时，其在3个轴的任意向量上的投影大小分别是x,y,z。

 

单位向量：在任意方向上大小为1的向量称作这个方向的单位向量。

向量相加：向量u(终点为x1,y1,z1)与向量v(x2,y2,z2)相加后仍然得到一个向量。其数学过程为。我们将这个向量称之为u与v的合向量。物理学中力的合成与分解就对应着向量的加法与投影，向量加法符合一个平行四边形定则大家应该不陌生。

向量相减：提到向量相减，不仿先说说负向量(或者向量取反)。由于向量既有大小又有方向，而大小是个标量，即可用实数表示，因此有正负。而方向呢又有正反两个方向，我们也用正负来表达。因此一个向量取反，我们可以认为是实数取反，也可以认为是方向取反。总之向量u取反后，-u与u的模相等，方向相反。因此向量u与v相减，我们可以认为是u与-v相加。

向量乘法：向量乘法有三种，分别是向量的数乘、向量的点乘和向量的叉乘。

数乘：一个标量k与一个向量u相乘得ku，ku仍然是一个向量。

当k>0时ku与u同向，反之反向;

点乘：点乘也叫做内积，其结果仍然是个向量。u·v可以分解为u在v的投影u’的模与v进行数乘。计算方法：。由于前面讲的我们可以分解为投影与数乘，因此点乘之后的模可以这样计算：。

点乘的特性：

这3个特性的好处是什么呢？我们看一下，由于计算内积只需要将终点的坐标依次相乘，而计算角度反而比较复杂，因此当我们只需要判断两个向量(两条直线也可以转化为两个单位向量)的夹角是垂直、钝角、锐角的时候，用这3个特性将非常的快。具体的应用场景也很多。

叉乘：叉乘也叫做外积，其结果仍然是个向量。

给定2个向量后，确定其叉乘的法相时，有左右手法则(3维坐标系是哪只手的坐标系则用哪只手来比划)。假如是左手坐标系，给定a和b，伸出你的左手，四指伸直朝向a的方向，大拇指与食指垂直，然后四指向掌心弯曲至b的方向，则大拇指指向的方向为叉乘向量的方向。上图给出的情况，左手比划出来大拇指朝上。如果将a b调换，那么我们需要将手翻过来，也就是大拇指向下。因此可知叉乘不满足交换律，一旦交换叉乘的顺序，则方向就会反向。我们称之为反对称性(反交换律)

 

 

矩阵

明天继续…………