所有结点对的最短路径问题之Johnson算法

Johnson算法可以在O(V*V lgV + VE)的时间内找到所有节点对之间的最短路径，对于稀疏图来说，算法的渐进表现要由于重复平方法和FloydWarshall算法，如果图没有权值为负值的环路，则返回所有结点对的最短路径权重的矩阵，否则，报告图有权值为负的环

算法中运用Diskra、BellmanFord算法，使用的技术是重新赋予权重，

如果图G = （V, E）中权值全为非负值，则通过对所有结点运行一次dijkstra算法找出所有结点对的最短路径，

如果有非负值，但没有权重为负值的环路，那么只要计算出一组新的非负权重值，然后再用相同的方法即可。

对于将负值权重转换为非负值使用的方法是，在原图上新加一个结点s，并将w(s, v) == 0， 然后对s运行BellmanFord函数计算出s到其他点的最短路径，

运用一个h[vexnum]数组存放这个值，h[i] = σ(s, v),即s到v的最短路径值。

这个值相当于将每个结点赋予一个一个值，这些值用于重新计算边的权重ww(u, v) = w(u, v) + h(u) - h(v),重新计算出来的权重即为非负值。

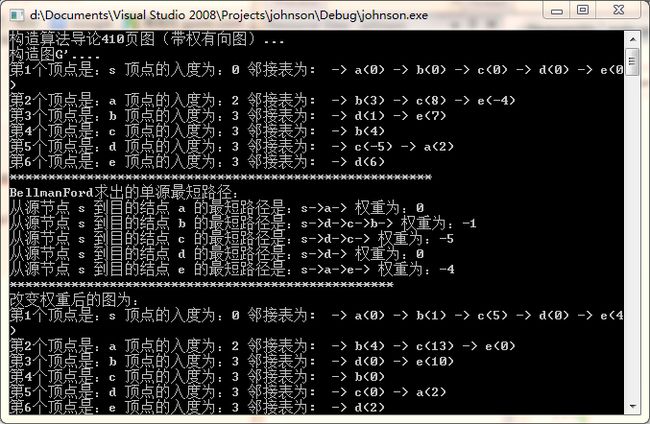
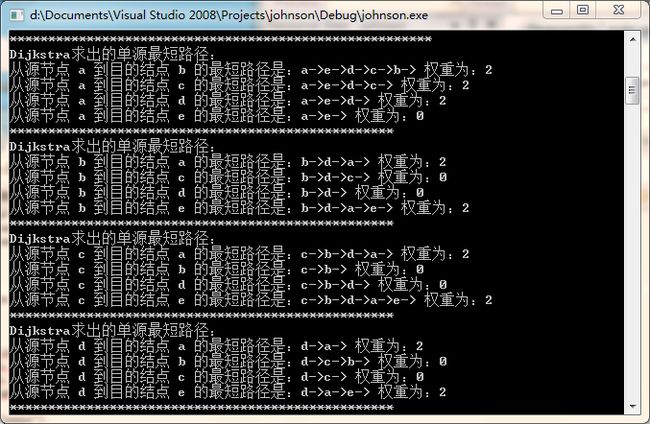
以下是代码的运行过程图，书410页：

以下为代码：

/************************************************************
Johnson.h: Johnson算法，存储为邻接表，
Date: 2014/1/5
Author: searchop
************************************************************/

#ifndef ALGRAPH_H
#define ALGRAPH_H

#include <vector>
#include <queue>
#include <stack>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;

//邻接表的结构
struct ArcNode          //表结点
{
	int source;        //图中该弧的源节点
	int adjvex;        //该弧所指向的顶点的位置
	ArcNode *nextarc;  //指向下一条弧的指针
	int weight;         //每条边的权重
};

template <typename VertexType>
struct VertexNode           //头结点
{
	VertexType data;    //顶点信息
	ArcNode *firstarc;  //指向第一条依附于该顶点的弧的指针
	int key;            //Prim:保存连接该顶点和树中结点的所有边中最小边的权重; 
	                    //BellmanFord:记录从源结点到该结点的最短路径权重的上界
	VertexNode *p;      //指向在树中的父节点
	int indegree;       //记录每个顶点的入度
};

const int SIZE = 6;

//图的操作
template <typename VertexType>
class ALGraph
{
public:
	typedef VertexNode<VertexType> VNode;
	ALGraph(int verNum) : vexnum(verNum), arcnum(0)
	{
		for (int i = 0; i < MAX_VERTEX_NUM; i++)
		{
			vertices[i].firstarc = NULL;
			vertices[i].key = INT_MAX/2;
			vertices[i].p = NULL;
			vertices[i].indegree = 0;
		}
	}

	//构造算法导论410页图（带权有向图）
	void createWDG()
	{
		cout << "构造算法导论410页图（带权有向图）..." << endl;
		int i;
		for (i = 1; i < vexnum; i++)
			vertices[i].data = 'a' + i - 1;		

		insertArc(1, 2, 3);
		insertArc(1, 3, 8);
		insertArc(1, 5, -4);
		insertArc(2, 4, 1);
		insertArc(2, 5, 7);
		insertArc(3, 2, 4);
		insertArc(4, 3, -5);
		insertArc(4, 1, 2);
		insertArc(5, 4, 6);
	}

	void createG()
	{
		cout << "构造图G'...." << endl;
        vertices[0].data = 's';
		insertArc(0, 1, 0);
		insertArc(0, 2, 0);
		insertArc(0, 3, 0);
		insertArc(0, 4, 0);
		insertArc(0, 5, 0);
	}

	//Johnson算法，先使用BellmanFord算法，使所有的边的权重变为非负值，
	//然后运用dijkstra算法求出结点对的最短路径
	int **Johnson()
	{
		createG();          //构造G’
		displayGraph();

		if (!BellmanFord(1))
		   cout << "the input graph contains a negative-weight cycle" << endl;
		else
		{
			int h[SIZE];
			int i, j, k;

			//将数组h[]的值设为运行BellmanFord后取得的值，h[i]为结点s到其他点的最短路径
			for (i = 0; i < vexnum; i++)
			    h[i] = vertices[i].key;
			//遍历所有的边，将边的权值重新赋值,即将所有的边的权值改为负值
			for (i = 0; i < vexnum; i++)
			{
				ArcNode *arc = vertices[i].firstarc;
				for (; arc != NULL; arc = arc->nextarc)
					arc->weight = arc->weight + h[arc->source] - h[arc->adjvex];
			}	
			以下为代码：
                        cout << "改变权重后的图为：" << endl;                                                                                                                     displayGraph();
			int **d = new int *[SIZE];
			for (j = 0; j < SIZE; j++)
				d[j] = new int[SIZE];
			//对每个结点运行dijkstra算法，求出每个点到其他点的最短路径，保存在key中
			for (k = 1; k < SIZE; k++)
			{
				Dijkstra(k+1);
				for (i = 1; i < SIZE; i++)
					d[k][i] = vertices[i].key + h[i] - h[k];
			}
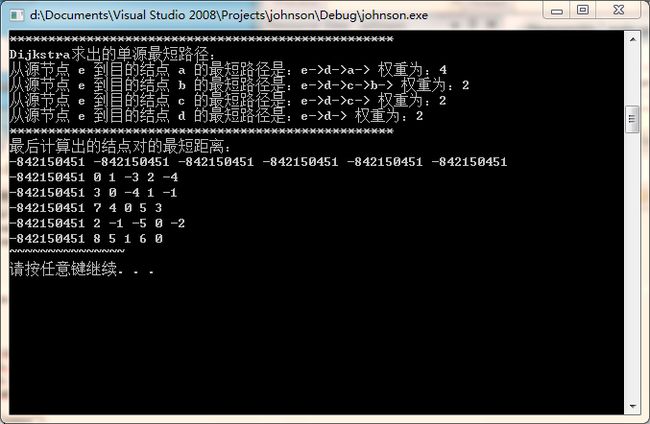
			cout << "最后计算出的结点对的最短距离：" << endl;
			displayTwoDimArray(d);
			return d;
		}
	}

	//输出一个二维数组
	void displayTwoDimArray(int **p)
	{
		for (int i = 0; i < SIZE; i++)
		{
			for (int j = 0; j < SIZE; j++)
				cout << p[i][j] << " ";
			cout << endl;
		}
		cout << "~~~~~~~~~~~~~~~" << endl;
	}

	//打印邻接链表
	virtual void displayGraph()
	{
		for (int i = 0; i < vexnum; i++)
		{
			cout << "第" << i+1 << "个顶点是：" << vertices[i].data
				<< " 顶点的入度为：" << vertices[i].indegree << " 邻接表为: ";
			ArcNode *arcNode = vertices[i].firstarc;
			while (arcNode != NULL)
			{
				cout << " -> " << vertices[arcNode->adjvex].data
					<< "(" << arcNode->weight << ")";
				arcNode = arcNode->nextarc;
			}
			cout << endl;
		}
		cout << "*******************************************************" << endl;
	}

	//PVnode排序准则
	class PVNodeCompare
	{
	public:
		bool operator() (VNode *pvnode1, VNode *pvnode2)
		{
			return pvnode1->key > pvnode2->key;
		}
	};

	//对每个结点的最短路径估计和前驱结点进行初始化，最短路径初始化为INT_MAX, p初始化为NULL
	//并将源节点的key初始化为0
	void InitalizeSingleSource(int index)
	{
		for (int i = 0; i < MAX_VERTEX_NUM; i++)
		{
			vertices[i].key = INT_MAX>>2;
			vertices[i].p = NULL;
		}
		vertices[index].key = 0;
	}

	//对边（u, v）进行松弛，将目前s到v的最短路径v.key与s到u的最短路径加上w(u, v)的值进行比较
	//如果比后面的值还大，则进行更新，将v.key缩短，并且将p置为u
	void relax(ArcNode *arc)
	{
		//竟然溢出了！！
		if (vertices[arc->adjvex].key > vertices[arc->source].key + arc->weight)
		{
			vertices[arc->adjvex].key = vertices[arc->source].key + arc->weight;
			vertices[arc->adjvex].p = &vertices[arc->source];
		}
	}

	//BellmanFord, index为实际第几个点
	bool BellmanFord(int index)
	{
		InitalizeSingleSource(index-1);
		for (int i = 1; i < vexnum; i++)     //循环共进行vexnum-1次
		{
			//遍历所有的边，并对每个边进行一次松弛
			for (int j = 0; j < vexnum; j++)
			{
				for (ArcNode *arc = vertices[j].firstarc; arc != NULL; arc = arc->nextarc)
					relax(arc);
			}
		}
		//再次遍历所有的边，检查图中是否存在权重为负值的环路，如果存在，则返回false
		for (int j = 0; j < vexnum; j++)
		{
			for (ArcNode *arc = vertices[0].firstarc; arc != NULL; arc = arc->nextarc)
			{
				if (vertices[arc->adjvex].key > vertices[arc->source].key + arc->weight)
					return false;
			}
		}
		cout << "BellmanFord求出的单源最短路径：" << endl;
		for (int i = 1; i < vexnum; i++)
		{
			printPath(index-1, i);
		}
		cout << "**************************************************" << endl;
		return true;
	}

	void Dijkstra(int index)
	{
		InitalizeSingleSource(index-1);
		vector<VNode> snode;       //保存已经找到最短路径的结点
		vector<VNode *> que;       //保存结点的指针的数组，用这个数组执行堆的算法

		//将结点指针进队列，形成以key为关键值的最小堆
		for (int i = 0; i < vexnum; i++)
			que.push_back(&(vertices[i]));
		//使que按照pvnodecompare准则构成一个最小堆
		make_heap(que.begin(), que.end(), PVNodeCompare());   

		while (que.empty() == false)
		{
			//将队列中拥有最小key的结点出队
			VNode *node = que.front();
			pop_heap(que.begin(), que.end(), PVNodeCompare());   //从堆中删除最小的结点，只是放到了vector的最后
			que.pop_back();      //将vector中的这个结点彻底删除，因为后面还要再排序一次，以免影响后面的堆排序，pop算法。
			snode.push_back(*node);
			for (ArcNode *arc = node->firstarc; arc != NULL; arc = arc->nextarc)
				relax(arc);
			make_heap(que.begin(), que.end(), PVNodeCompare());
		}
		cout << "Dijkstra求出的单源最短路径：" << endl;
		for (int i = 1; i < vexnum; i++)
		{
			if (i != index-1)
			   printPath(index-1, i);
		}
		cout << "**************************************************" << endl;
	}

protected:
	//插入一个表结点
	void insertArc(int vHead, int vTail, int weight)
	{
		//构造一个表结点
		ArcNode *newArcNode = new ArcNode;
		newArcNode->source = vHead;
		newArcNode->adjvex = vTail;
		newArcNode->nextarc = NULL;
		newArcNode->weight = weight;

		//arcNode 是vertics[vHead]的邻接表
		ArcNode *arcNode = vertices[vHead].firstarc;
		if (arcNode == NULL)
			vertices[vHead].firstarc = newArcNode;
		else
		{
			while (arcNode->nextarc != NULL)
			{
				arcNode = arcNode->nextarc;		
			}
			arcNode->nextarc = newArcNode;
		}
		arcnum++;
		vertices[vTail].indegree++;         //对弧的尾结点的入度加1
	}

	//打印源节点到i的最短路径
	void printPath(int i, int j)
	{
		cout << "从源节点 " << vertices[i].data << " 到目的结点 "
			<< vertices[j].data << " 的最短路径是：" /*<< endl*/;
		__printPath(&vertices[i], &vertices[j]);
		cout << " 权重为：" << vertices[j].key << endl;
	}

	void __printPath(VNode* source, VNode* dest)
	{
		if (source == dest)
			cout << source->data << "->";
		else if (dest->p == NULL)
			cout << " no path！" << endl;
		else
		{
			__printPath(source, dest->p);
			cout << dest->data << "->";
		}
	}

private:
	//const数据成员必须在构造函数里初始化
	static const int MAX_VERTEX_NUM = 20;  //最大顶点个数

	VNode vertices[MAX_VERTEX_NUM];      //存放结点的数组
	int vexnum;             //图的当前顶点数
	int arcnum;             //图的弧数
};

#endif

#include "johnson.h"

int main()
{
	ALGraph<char> wdgGraph(6);
	wdgGraph.createWDG();
	wdgGraph.Johnson();
	/*wdgGraph.displayGraph();*/

	system("pause");
	return 0;
}

运行结果为:

运行时间分析：

BellmanFord的运行时间为O（V*E）

Dijkstra运用斐波那契堆来实现的话为O(VlgV + E),总共运行V次，则为O(V*VlgV + VE)

所以Johnson算法运行时间为以下为代码：O(V*VlgV + VE)

以下为代码：