面试笔试杂项积累
1.LIFO与FIFO
Last In First Out 后进先出
First Input First Output先进先出
2.汉诺塔
汉诺塔最少歩数
假如说有一个盘子的话,只需挪动一步;
假如说有n个盘子要挪An步,那么有n+1个盘子可以先通过An步把上面的n个盘子挪到第三个柱子上,再挪最大的盘子,最后把n个盘子挪到大的上面,共2An+1步,所以A(n+1)=2An+1
这样计算下来An=2^n-1(2的n次方减1)
3.自底向上与自顶向下
自底向上
自顶向下
4.HashTable&Dictionary
1.HashTable
哈希表(HashTable)表示键/值对的集合。在.NET Framework中,Hashtable是System.Collections命名空间提供的一个容器,用于处理和表现类似key-value的键值对,其中key通常可用来快速查找,同时key是区分大小写;value用于存储对应于key的值。Hashtable中key-value键值对均为object类型,所以Hashtable可以支持任何类型的keyvalue键值对,任何非 null 对象都可以用作键或值。
在哈希表中添加一个key/键值对:Hashtable.Add(key,);
在哈希表中去除某个key/键值对:HashtableRemove(key);
从哈希表中移除所有元素: Hashtable.Clear();
判断哈希表是否包含特定键key: Hashtable.Contains(key);
public virtual void Add(object key, object value);
[ReliabilityContract(Consistency.WillNotCorruptState, Cer.Success)]
public virtual void Clear();
public virtual object Clone();
public virtual bool Contains(object key);
public virtual bool ContainsKey(object key);
public virtual bool ContainsValue(object value);
public virtual void CopyTo(Array array, int arrayIndex);
public virtual IDictionaryEnumerator GetEnumerator();
protected virtual int GetHash(object key);
public virtual void GetObjectData(SerializationInfo info, StreamingContext context);
protected virtual bool KeyEquals(object item, object key);
public virtual void OnDeserialization(object sender);
[ReliabilityContract(Consistency.WillNotCorruptState, Cer.MayFail)]
public virtual void Remove(object key);
public static Hashtable Synchronized(Hashtable table);
2.Dictionary
Dictionary表示键和值的集合。
Dictionary<string, string>是一个泛型
他本身有集合的功能有时候可以把它看成数组
他的结构是这样的:Dictionary<[key], [value]>
他的特点是存入对象是需要与[key]值一一对应的存入该泛型
通过某一个一定的[key]去找到对应的值
public void Add(TKey key, TValue value);
public void Clear();
public bool ContainsKey(TKey key);
public bool ContainsValue(TValue value);
public Dictionary<TKey, TValue>.Enumerator GetEnumerator();
public virtual void GetObjectData(SerializationInfo info, StreamingContext context);
public virtual void OnDeserialization(object sender);
public bool Remove(TKey key);
public bool TryGetValue(TKey key, out TValue value);
4.HashTable和Dictionary的区别:
(1).HashTable不支持泛型,而Dictionary支持泛型。此处区别同ArrayList与List的区别
(2). Hashtable 的元素属于 Object 类型,所以在存储或检索值类型时通常发生装箱和拆箱的操作,所以你可能需要进行一些类型转换的操作,而且对于int,float这些值类型还需要进行装箱等操作,非常耗时。此处区别同ArrayList与List的区别
(3).单线程程序中推荐使用 Dictionary, 有泛型优势, 且读取速度较快, 容量利用更充分。多线程程序中推荐使用 Hashtable, 默认的 Hashtable 允许单线程写入, 多线程读取, 对 Hashtable 进一步调用 Synchronized() 方法可以获得完全线程安全的类型. 而 Dictionary 非线程安全, 必须人为使用 lock 语句进行保护, 效率大减。
(4)在通过代码测试的时候发现key是整数型Dictionary的效率比Hashtable快,如果key是字符串型,Dictionary的效率没有Hashtable快。难道是散列函数/哈希函数(地址映射函数)不同的原因?
简单的说:
装箱:就是将值类型的数据打包到引用类型的实例中
比如将string类型的值abc赋给object对象obj
String i=”abc”;
object obj=(object)i;
拆箱:就是从引用数据中提取值类型
比如将object对象obj的值赋给string类型的变量i
object obj=”abc”;
string i=(string)obj;
5.跳表SkipList
聊一聊作者的其人其事
跳表是由William Pugh发明。他在 Communications of the ACM June 1990, 33(6) 668-676 发表了Skip lists: a probabilistic alternative to balanced trees,在该论文中详细解释了跳表的数据结构和插入删除操作。
<2>. 言归正传,跳表简介
这是跳表的作者,上面介绍的William Pugh给出的解释:
Skip lists are a data structure that can be used in place of balanced trees.Skip lists use probabilistic balancing rather than strictly enforced balancingand as a result the algorithms for insertion and deletion in skip lists aremuch simpler and significantly faster than equivalent algorithms forbalanced trees.
跳表是平衡树的一种替代的数据结构,但是和红黑树不相同的是,跳表对于树的平衡的实现是基于一种随机化的算法的,这样也就是说跳表的插入和删除的工作是比较简单的。
下面来研究一下跳表的核心思想:
先从链表开始,如果是一个简单的链表,那么我们知道在链表中查找一个元素I的话,需要将整个链表遍历一次。
如果是说链表是排序的,并且节点中还存储了指向前面第二个节点的指针的话,那么在查找一个节点时,仅仅需要遍历N/2个节点即可。
这基本上就是跳表的核心思想,其实也是一种通过“空间来换取时间”的一个算法,通过在每个节点中增加了向前的指针,从而提升查找的效率。
<3>.跳表的数据存储模型
我们定义:
如果一个基点存在k个向前的指针的话,那么陈该节点是k层的节点。
一个跳表的层MaxLevel义为跳表中所有节点中最大的层数。
下面给出一个完整的跳表的图示:
像这个3,6,7,9都是随机的
http://www.cnblogs.com/xuqiang/archive/2011/05/22/2053516.html
6.Hash Table哈希表(散列表)
http://baike.baidu.com/link?url=AIG3wqmNPfqOq5KG7DvgOjewShPo15C7o9kde5BqyONJQmsLh144OeKG1nhljQgESqP-vI2I-da4WYLq9IsLEq
基本概念
-
若关键字为 k,则其值存放在 f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系 f为散列函数,按这个思想建立的表为散列表。 散列函数/哈希函数(地址映射函数)
-
对不同的关键字可能得到同一散列地址,即 k1≠k2,而 f(k1)=f(k2),这种现象称为碰撞(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数 f(k)和处理碰撞的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
-
若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个 “随机的地址”,从而减少碰撞。
7.随机存取
自然也有顺序存取
在计算机科学中,随机存取(有时亦称直接访问)代表同一时间访问一组序列中的一个随意组件。反之则称循序访问,即是需要更多时间去访问一个远程组件。随机存取存储器的基本结构可分为三个部分:存储矩阵,地址译码器,读写电路。
8.c#运算符重载
http://www.cnblogs.com/LilianChen/archive/2013/03/15/2961901.html
运算符重载允许为运算指定用户定义的运算符实现,其中一个或两个操作数是用户定义的类或结构类型。用户定义的运算符实现的优先级总是高于预定义运算符实现:仅当没有适用的用户定义运算符实现时才会考虑预定义运算符实现。
| 运算符 |
可重载性 |
| +、-、!、~、++、--、true、false |
可以重载这些一元运算符。 |
| +、-、*、/、%、&、|、^、<<、>> |
可以重载这些二元运算符。 |
| ==、!=、<、>、<=、>= |
可以重载比较运算符。必须成对重载。 |
| &&、|| |
不能重载条件逻辑运算符。 |
| [] |
不能重载数组索引运算符,但可以定义索引器。 |
| () |
不能重载转换运算符,但可以定义新的转换运算符。 |
| +=、-=、*=、/=、%=、&=、|=、^=、<<=、>>= |
不能显式重载赋值运算符。 |
| =、.、?:、->、new、is、sizeof、typeof |
不能重载这些运算符。 |
下面的例子中Vector结构表示一个三维矢量:
1 using System; 2 3 namespace ConsoleApplication19 4 { 5 class Program 6 { 7 static void Main(string[] args) 8 { 9 Vector vect1, vect2, vect3; 10 vect1 = new Vector(3.0, 3.0, 1.0); 11 vect2 = new Vector(2.0, -4.0, -4.0); 12 vect3 = vect1 + vect2; 13 14 Console.WriteLine("vect1=" + vect1.ToString()); 15 Console.WriteLine("vect2=" + vect2.ToString()); 16 Console.WriteLine("vect3=" + vect3.ToString()); 17 Console.ReadLine(); 18 } 19 } 20 21 struct Vector 22 { 23 public double x, y, z; 24 25 public Vector(double x, double y, double z) 26 { 27 this.x = x; 28 this.y = y; 29 this.z = z; 30 } 31 32 public Vector(Vector rhs) 33 34 { 35 this.x = rhs.x; 36 this.y = rhs.y; 37 this.z = rhs.z; 38 } 39 40 public override string ToString() 41 { 42 return "(" + x + "," + y + "," + z + ")"; 43 } 44 45 public static Vector operator +(Vector lhs, Vector rhs) 46 { 47 Vector result = new Vector(lhs); 48 result.x += rhs.x; 49 result.y += rhs.y; 50 result.z += rhs.z; 51 return result; 52 } 53 } 54 }
- 运算符重载的声明方式:operator关键字告诉编译器,它实际上是一个运算符重载,后面是相关运算符的符号
- 对于二元运算符,第一个参数是放在运算符左边的值,一般命名为lhs;第二个参数是放在运算符右边的值,一般命名为rhs
- C#要求所有的运算符重载都声明为public和static,这表示它们与它们的类或结构相关联,而不是与实例相关联。
添加重载乘法运算符:
1 public static Vector operator *(double lhs, Vector rhs) 2 { 3 return new Vector(lhs * rhs.x, lhs * rhs.y, lhs * rhs.z); 4 }
如果a和b声明为Vector类型,就可以编写代码:b=2*a; 编译器会隐式的把整数2转换为double类型,但是不能编译代码:b=a*2;
比较运算符的重载:
- C#要求成对重载比较运算符,如果重载了==,也必须重载!=,否在会产生编译错误。
- 比较运算符必须返回bool类型的值
- 注意:在重载==和!=时,还应该重载从System.Object中继承的Equals()和GetHashCode()方法,否则会产生一个编译警告,原因是Equals方法应执行与==运算符相同的相等逻辑。
下面给Vector结构重载==和!=运算符:
1 public static bool operator ==(Vector lhs, Vector rhs) 2 { 3 if (lhs.x == rhs.x && lhs.y == rhs.y && lhs.z == rhs.z) 4 { 5 return true; 6 } 7 else 8 { 9 return false; 10 } 11 }
1 public static bool operator !=(Vector lhs, Vector rhs) 2 { 3 return !(lhs == rhs); 4 }
重载True和False运算符:
1 using System; 2 3 namespace ConsoleApplication20 4 { 5 class Program 6 { 7 static void Main(string[] args) 8 { 9 // 输出20以内的所有素数 10 for (uint i = 2; i <= 20; i++) 11 { 12 Prime p = new Prime(i); 13 if (p) 14 { 15 Console.Write(i + " "); 16 } 17 } 18 Console.ReadLine(); 19 } 20 } 21 22 public struct Prime 23 { 24 private uint value; 25 public Prime(uint value) 26 { 27 this.value = value; 28 } 29 30 public static bool operator true(Prime p) 31 { 32 return IsPrime(p.value); 33 } 34 35 public static bool operator false(Prime p) 36 { 37 return !(IsPrime(p.value)); 38 } 39 40 public static bool IsPrime(uint value) 41 { 42 for (uint i = 2; i <= value / 2; i++) 43 { 44 if (value % i == 0) 45 { 46 return false; 47 } 48 } 49 return true; 50 } 51 52 public override string ToString() 53 { 54 return ("" + value); 55 } 56 } 57 }
1 using System; 2 3 namespace ConsoleApplication21 4 { 5 class Program 6 { 7 static void Main(string[] args) 8 { 9 DBBool b; 10 b = DBBool.dbTrue; 11 if (b) 12 { 13 Console.WriteLine("b is definitely true"); 14 } 15 else 16 { 17 Console.WriteLine("b is not definitely true"); 18 } 19 Console.ReadLine(); 20 } 21 } 22 23 public struct DBBool 24 { 25 public static readonly DBBool dbNull = new DBBool(0); 26 public static readonly DBBool dbFalse = new DBBool(-1); 27 public static readonly DBBool dbTrue = new DBBool(1); 28 29 int value; 30 31 DBBool(int value) 32 { 33 this.value = value; 34 } 35 36 public static bool operator true(DBBool x) 37 { 38 return x.value > 0; 39 } 40 41 public static bool operator false(DBBool x) 42 { 43 return x.value < 0; 44 } 45 } 46 }
9.二叉树的先序中序后序遍历
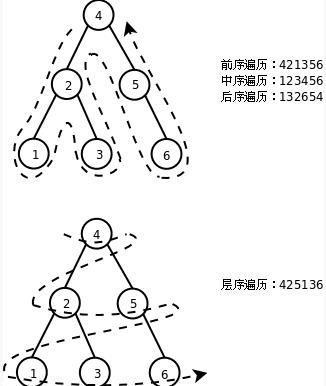
10.二叉树的层次遍历与广度优先遍历(递归)
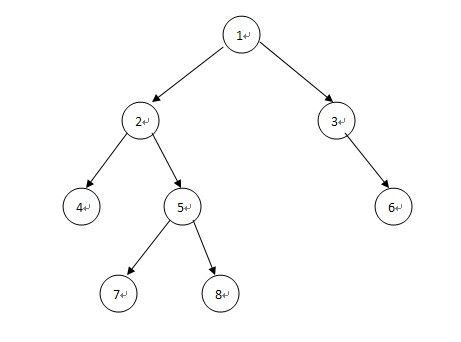
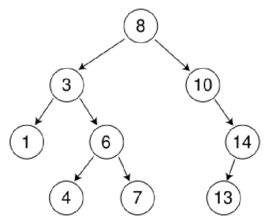
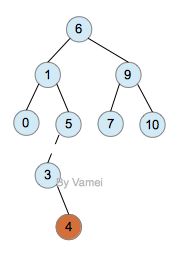
给定一棵二叉树,要求进行分层遍历,每层的节点值单独打印一行,下图给出事例结构:
对此二叉树遍历的结果应该是:
1,
2 , 3
4, 5, 6
7, 8
第一种方法,就是利用递归的方法,按层进行打印,我们把根节点当做第0层,之后层次依次增加,如果我们想打印第二层怎么办呢,利用递归的代码如下:
如果我们成功的打印了给定的层次,那么就返回非0的正值,如果失败返回0。有了这个思路,我们就可以应用一个循环,来打印这颗树的所有层的节点,但是有个问题就是我们不知道这棵二叉树的深度,怎么来控制循环使其结束呢,仔细看一下print_at_level,如果指定的Tree是空的,那么就直接返回0,当返回0的时候,我们就结束循环,说明没有节点可以打印了。
void print_by_level_1(Tree T) {
int i = 0;
for (i = 0; ; i++) {
if (!print_at_level(T, i))
break;
}
cout << endl;
}
还有另一种广度优先遍历的方法就是使用一个队列queue
11.二叉树的深度(递归)
为了求得树的深度,可以先求左右子树的深度,取二者较大者加1即是树的深度,递归返回的条件是若节点为空,返回0
算法:
堆也是一棵完全二叉树
13.二叉树的广度优先遍历和深度优先遍历(非递归)
http://blog.csdn.net/kuailekemi/article/details/9234269深度优先
void DepthFirstTravel(Tree *root)
{
stack<Tree *> s;
s.push(root);
while(!s.empty())
{
root = s.top();
cout << root->data << " ";
s.pop();
if(root->rchild != NULL)
{
s.push(root->rchild);
}
if(root->lchild != NULL)
{
s.push(root->lchild);
}
}
}
广度优先
void BreadthFirstTravel(Tree *root)
{
queue<Tree *> q;
q.push(root);
while(!q.empty())
{
root = q.front();
cout << root->data << " ";
q.pop();
if(root->lchild != NULL)
{
q.push(root->lchild);
}
if(root->rchild != NULL)
{
q.push(root->rchild);
}
}
}
这些看上去挺简单的,但是,在我们头脑中越是简单的东西,我们的大脑越是喜欢忽视,所以,有必要加强一下。
14.c#自定义泛型类
Generic是Framework 2.0的新元素,中文名字称之为“泛型” ,特征是一个带有尖括号的类,比如List< T>
C#自定义泛型类用得最广泛,就是集合(Collection)中。实际上,泛型的产生其中一个原因就是为了解决原来集合类中元素的装箱和拆箱问题(如果对装箱和拆箱概念不明,请百度搜索)。由于泛型的使用,使得集合内所有元素都属于同一类,这就把类型不同的隐患消灭在编译阶段——如果类型不对,则编译错误。
这里只讨论C#自定义泛型类。基本自定义如下:
public class MyGeneric < T>
...{
private T member;
public void Method (T obj)
...{
}
}
这里,定义了一个泛型类,其中的T作为一个类,可以在定义的类中使用。当然,要定义多个泛型类,也没有问题。
public class MyGeneric < TKey, TValue>
...{
private TKey key;
private TValue value;
public void Method (TKey k, TValue v)
...{
}
}
泛型的初始化:泛型是需要进行初始化的。使用T doc = default(T)以后,系统会自动为泛型进行初始化。
限制:如果我们知道,这个将要传入的泛型类T,必定具有某些的属性,那么我们就可以在MyGeneric< T>中使用T的这些属性。这一点,是通过interface来实现的。
// 先定义一个interface
public interface IDocument
...{
string Title ...{get;}
string Content ...{get;}
}
// 让范型类T实现这个interface
public class MyGeneric < T>
where T : IDocument
...{
public void Method(T v)
...{
Console.WriteLine(v.Title);
}
}
// 传入的类也必须实现interface
public class Document : IDocument
...{
......
}
// 使用这个泛型
MyGeneric< Document> doc = new MyGeneric< Document>();
泛型方法:我们同样可以定义泛型的方法
void Swap< T> (ref T x, ref T y)
...{
T temp = x;
x = y;
y = temp;
}
泛型代理(Generic Delegate):既然能够定义泛型方法,自然也可以定义泛型代理
public delegate void delegateSample < T> (ref T x, ref T y)
private void Swap (ref T x, ref T y)
...{
T temp = x;
x = y;
y = temp;
}
// 调用
public void Run()
...{
int i,j;
i = 3;
j = 5;
delegateSample< int> sample = new delegateSample< int> (Swap);
sample(i, j);
}
设置可空值类型:一般来说,值类型的变量是非空的。但是,Nullable< T>可以解决这个问题。
Nullable< int> x; // 这样就设置了一个可空的整数变量x
x = 4;
x += 3;
if (x.HasValue) // 使用HasValue属性来检查x是否为空
...{ Console.WriteLine ("x="+x.ToString());
}
x = null; // 可设空值
使用ArraySegment< T>来获得数组的一部分。如果要使用一个数组的部分元素,直接使用ArraySegment来圈定不失为一个不错的办法。
int[] arr = ...{1, 2, 3, 4, 5, 6, 7, 8, 9};
// 第一个参数是传递数组,第二个参数是起始段在数组内的偏移,第三个参数是要取连续多少个数
ArraySegment< int> segment = new ArraySegment< int>(arr, 2, 3); // (array, offset, count)
for (int i = segment.Offset; i< = segment.Offset + segment.Count; i++)
...{
Console.WriteLine(segment.Array[i]); // 使用Array属性来访问传递的数组
}
在例子中,通过将Offset属性和Count属性设置为不同的值,可以达到访问不同段的目的。
以上就是C#自定义泛型类的用法介绍。
15.LZW压缩算法
http://blog.csdn.net/abcjennifer/article/details/7995426
16.优先队列
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (largest-in,first-out)的行为特征。优先队列是队列的一种,不过它可以按照自定义的一种方式(数据的优先级)来对队列中的数据进行动态的排序
每次的push和pop操作,队列都会动态的调整,以达到我们预期的方式来存储。
例如:我们常用的操作就是对数据排序,优先队列默认的是数据大的优先级高
所以我们无论按照什么顺序push一堆数,最终在队列里总是top出最大的元素。
http://www.cnblogs.com/void/archive/2012/02/01/2335224.html
17.左高树
18.堆与堆排序
http://blog.csdn.net/morewindows/article/details/6709644/
堆排序与快速排序,归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前,先讲解下什么是数据结构中的二叉堆。
二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
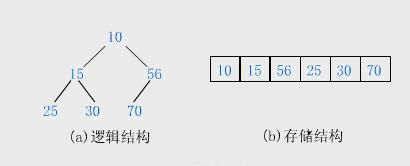
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。
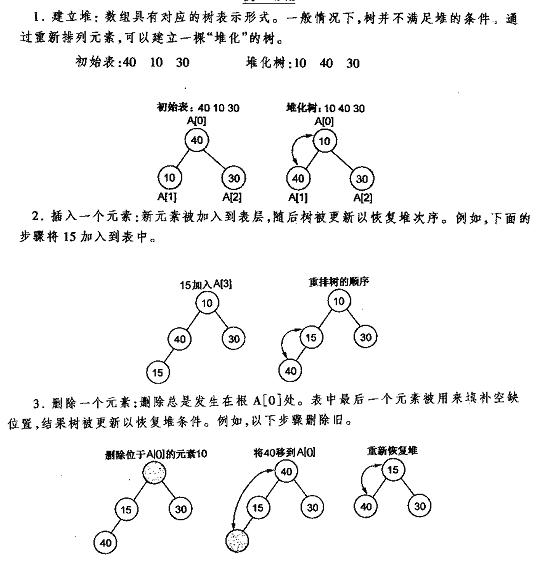
堆的操作——插入删除
下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解,再给出本人的实现代码,最好是先看明白图后再去看代码。
堆的插入
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中,对照《白话经典算法系列之二 直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码:
更简短的表达为:
插入时:
堆的删除
按定义,堆中每次都只能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码:
堆化数组
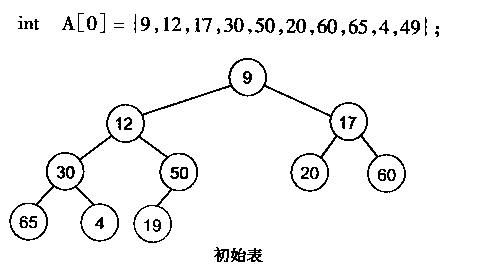
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
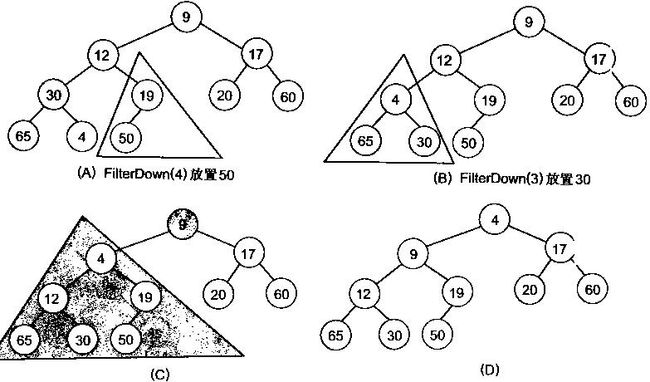
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
写出堆化数组的代码:
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
MinHeapFixdown(a, i, n);
}
至此,堆的操作就全部完成了(注1),再来看下如何用堆这种数据结构来进行排序。
堆排序
首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
由于堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
注意使用最小堆排序后是递减数组,要得到递增数组,可以使用最大堆。
由于每次重新恢复堆的时间复杂度为O(logN),共N - 1次重新恢复堆操作,再加上前面建立堆时N / 2次向下调整,每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数,可以参阅《STL系列之四 heap 堆》。
注1 作为一个数据结构,最好用类将其数据和方法封装起来,这样即便于操作,也便于理解。此外,除了堆排序要使用堆,另外还有很多场合可以使用堆来方便和高效的处理数据,以后会一一介绍。
19.贪心算法
20.二叉查找树/二叉搜索树/二叉排序树
http://blog.csdn.net/npy_lp/article/details/7426431
二叉查找树
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
3、二叉查找树的基本运算
(1)、插入
在二叉查找树中插入新结点,要保证插入新结点后仍能满足二叉查找树的性质。例子中的插入过程如下:
a、若二叉查找树root为空,则使新结点为根;
b、若二叉查找树root不为空,则通过search_bst_for_insert函数寻找插入点并返回它的地址(若新结点中的关键字已经存在,则返回空指针);
c、若新结点的关键字小于插入点的关键字,则将新结点插入到插入点的左子树中,大于则插入到插入点的右子树中。
中序遍历二叉查找树可得到一个关键字的有序序列。(从小到大)
(3)、删除
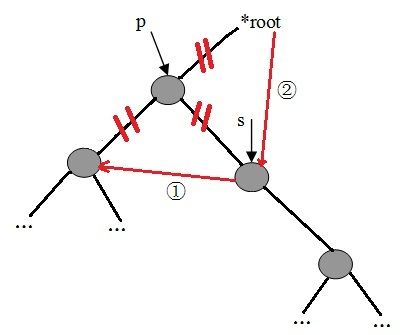
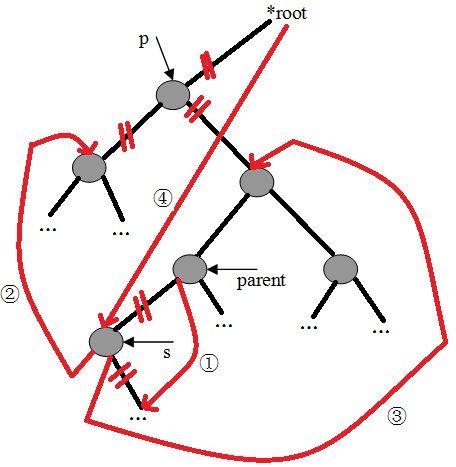
删除某个结点后依然要保持二叉查找树的特性。例子中的删除过程如下:
a、若删除点是叶子结点,则设置其双亲结点的指针为空。
b、若删除点只有左子树,或只有右子树,则设置其双亲结点的指针指向左子树或右子树。
c、若删除点的左右子树均不为空,则:
1)、查询删除点的右子树的左子树是否为空,若为空,则把删除点的左子树设为删除点的右子树的左子树。
2)、若不为空,则继续查询左子树,直到找到最底层的左子树为止。
4、二叉查找树的查找分析
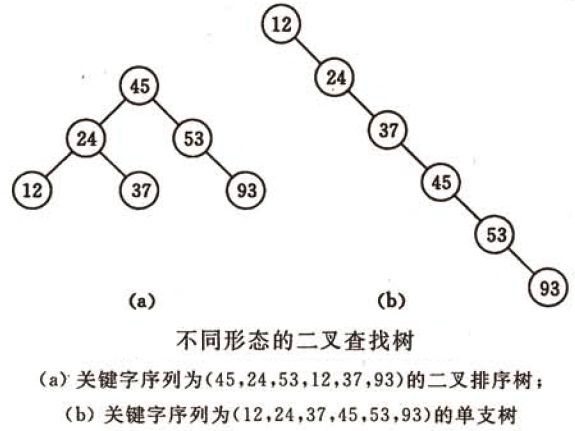
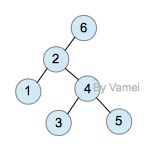
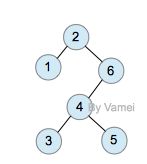
同样的关键字,以不同的插入顺序,会产生不同形态的二叉查找树。
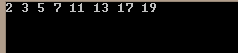
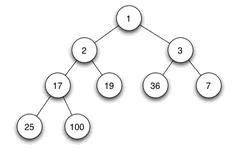
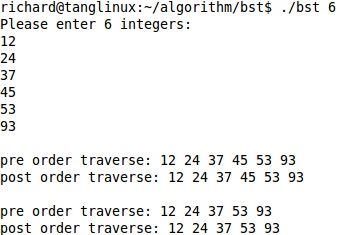
运行两次,以不同的顺序输入相同的六个关键字:
根据前序遍历的结果可得到两次运行所产生的二叉查找树的形态并不相同,如下图:
20.索引二叉查找树/索引二叉搜索树
节点的值域是三元的,相比于key、value多了leftSize,leftSize是该节点左子树的元素个数21.赢者树与败者树/竞赛树
http://www.geeksforgeeks.org/tournament-tree-and-binary-heap/
形象来说,外部节点表示选手捉对厮杀,内部节点表示比赛的胜者(败者)。定义如下:对于n名选手,赢者树是一棵含n个外部节点,n-1个内部节点的完全二叉树,其中每个内部节点记录了相应赛局的赢家(或输家)。
22.内部排序与外部排序
http://baike.baidu.com/link?url=tsuqzZTG9JQvOtmG-AjnN_wv8ms9MsEH-4L7pzi4WZ75rOGrCcz4RfKa1u45nFcJlt5fAkaFAZHUNAABI5OMJq
一般提到排序都是指内排序,比如快速排序,堆排序,归并排序等,所谓内排序就是可以在内存中完成的排序。RAM的访问速度大约是磁盘的25万倍,我们当然希望如果可以的话都是内排来完成。但对于大数据集来说,内存是远远不够的,这时候就涉及到外排序的知识了。
内部排序
http://blog.csdn.net/luxiaoxun/article/details/7824455
外部排序
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装入内存的部分分别把每一部分调入内存完成排序。然后,对已经排序的子文件进行归并排序。
23.哈夫曼树与哈夫曼编码(霍夫曼)
http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html
在一般的数据结构的书中,树的那章后面,著者一般都会介绍一下哈夫曼(HUFFMAN)
树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛,如
JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树,
是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点
的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度
为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln)
,N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径
长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
24.NP问题(Non-deterministic Polynomial)
http://baike.baidu.com/link?url=MAC3OxxVfut5gPJMAieijsciZoSligWIWrqg_Tn9flWqFmP44fSlrg-qfvVBVKtqka0amv8ZZvAvex5RKaI4Pa
NP完全问题(NP-C问题),是世界七大数学难题之一。 NP的英文全称是Non-deterministic Polynomial的问题,即多项式复杂程度的非确定性问题。简单的写法是 NP=P?,问题就在这个问号上,到底是NP等于P,还是NP不等于P。
25.隐式数据结构(Implicit data structure)
https://en.wikipedia.org/wiki/Implicit_data_structure优先级队列是一种隐式数据结构
26.数据域与指针域
一般是在链表中的结点,数据域存放数据,指针域存放指向下一个结点的指针,以实现链表彻底线型结构。链表有单链表,双向链表以及循环链表等。
27.AVL平衡二叉查找树
我们在树, 二叉树, 二叉搜索树中提到,一个有n个节点的二叉树,它的最小深度为log(n),最大深度为n。比如下面两个二叉树:
深度为n的二叉树
深度为log(n)的二叉树
这两个二叉树同时也是二叉搜索树(参考树, 二叉树, 二叉搜索树)。注意,log以2为基底。log(n)是指深度的量级。根据我们对深度的定义,精确的最小深度为floor(log(n)+1)。
我们将处于同一深度的节点归为一层。如果除最后一层外的其他层都被节点填满时,二叉树有最小深度log(n)。
二叉搜索树的深度越小,那么搜索所需要的运算时间越小。一个深度为log(n)的二叉搜索树,搜索算法的时间复杂度也是log(n)。然而,我们在二叉搜索树中已经实现的插入和删除操作并不能让保持log(n)的深度。如果我们按照8,7,6,5,4,3,2,1的顺序插入节点,那么就是一个深度为n的二叉树。那么,搜索算法的时间复杂度为n。
n和log(n)的时间复杂度意味着什么呢?时间复杂度代表了完成算法所需要的运算次数。时间复杂度越小,算法的速度越快。
可以看到,随着元素的增加,log(n)的时间复杂度的增长要远小于n。所以,我们自然希望二叉搜索树能尽可能保持log(n)的深度。在上面深度为n的例子中,我们发现,每个节点只有左节点被填满。树的每一层都有很多空位。能不能尽可能减少每一层的空位呢? (相应的,减少树的深度)
“紧致”的树
一种想法是先填满一层,再去填充下一层,这样就是一个完全二叉树(complete binary tree)。这样的二叉树实现插入算法会比较复杂。我们将介绍一种思路相似,但比较容易实现的树状数据结构——AVL树。
AVL树
AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Landis命名的。它是一种特殊的二叉搜索树。AVL树要求: 任一节点的左子树深度和右子树深度相差不超过1
(空树的深度为0。注意,有的教材中,采用了不同的深度定义方法,所以空树的深度为-1)
下面是AVL树:
AVL树
AVL树的特性让二叉搜索树的节点实现平衡(balance):节点相对均匀分布,而不是偏向某一侧。因此,AVL树的搜索算法复杂度是log(n)的量级。
我们在二叉搜索树中定义的操作,除了插入,都可以用在AVL树上 (假设使用懒惰删除)。如果进行插入操作,有可能会破坏AVL树的性质,比如:
插入2: 破坏AVL树
观察节点5,它的左子树深度为2,右子树深度为0,所以左右两个子树深度相差为2,不再是AVL树。由于2的加入,从节点6,1,5,3到2的层数都增加1。6, 1, 5节点的AVL性质都被破坏。如果从节点2向上回溯,节点5是第一个被破坏的。从节点3开始的子树深度加1,这是造成6, 1, 5的AVL性质被破坏的本质原因。我们将5和3之间的路径画成虚线(就好像挂了重物,边被拉断一样)。
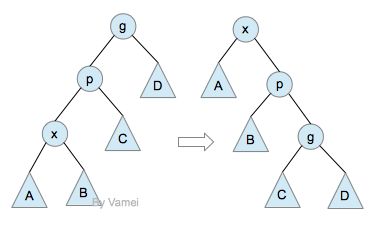
我们可以通过单旋照(single rotation),调整以5为根节点的子树,来修正因为插入一个元素而引起的对AVL性质的破坏。如下:
Single rotation: 左侧超重,向右转
通过单旋转,3成为新的根节点,2,5称为3的左右子节点。子树重新成为AVL树。该子树的深度减小1,这将自动修正2带给节点6,1的“超负荷”。
单旋转效果如下:
特别要注意的是,为了保持二叉树的性质,子树B过继给了节点5。
向左单旋转与之类似。作为练习,可以尝试绘制向左单旋转的示意图。
但如果插入的节点不是2,而是4,会是如何呢?
插入4
尝试单旋转,会发现无法解决问题。以5为根节点的子树向右单旋转后,树将以3为根节点,4,5为子节点。4比3大,却是3的左子节点,显然,这依然不符合二叉搜索树的性质。但基于和上面相似的原则(调整以5为根节点的树),我们发现有一个简单的解决方式:
double rotation
上面的操作被称作双旋转(double rotation)。双旋转实际上是进行两次单旋转: 4为根节点的子树先进行一次向左的单旋转,然后将5为根节点的子树进行了一次向右的单旋转。这样恢复了树的ACL性质。
对于AVL树,可以证明,在新增一个节点时,总可以通过一次旋转恢复AVL树的性质。
当我们插入一个新的节点时,在哪里旋转?是用单旋转还是双旋转?
我们按照如下基本步骤进行:
1. 按照二叉搜索树的方式增加节点,新增节点称为一个叶节点。
2. 从新增节点开始,回溯到第一个失衡节点(5)。
(如果回溯到根节点,还没有失衡节点,就说明该树已经符合AVL性质。)
3. 找到断的边(5->3),并确定断弦的方向(5的左侧)
4. 以断边下端(3)为根节点,确定两个子树中的哪一个深度大(左子树还是右子树)。
(这两棵子树的深度不可能相等,而且深度大的子树包含有新增节点。想想为什么)
5. 如果第2和第3步中的方向一致(都为左或者都为右),需要单旋转以失衡节点为根节点的子树。
否则,双旋转以失衡节点为根节点的子树。
http://www.cnblogs.com/vamei/archive/2013/03/21/2964092.html
28.红黑树平衡二叉查找树
http://blog.chinaunix.net/uid-27767798-id-3339483.htmlhttp://blog.chinaunix.net/uid-26575352-id-3061918.html
红黑树是一种二叉查找树,它是在1972年由Rudolf Bayer发明的,它的性能优于平衡2叉树(avl树),因为avl树过分追求平衡,avl树要求任何节点的左右子树高度之差不能大于1,而红黑树做到的是任何节点的左右子
树高度差不会超过2倍(左子树的高度不会大于右子树高度的2倍,或者右子树的高度不会大于左子树的高度的2倍),由此看出avl树如果要保持平衡需要付出更多的旋转(左旋,右旋),avl更平衡意味着avl树比红黑树的高度更低,查询时更快一些,但是过多旋转的时间代价大于查询带来的优势。红黑树的应用:jdk中的treeMap,内核中CFS调度根据vruntime(虚拟运行时间),来为进程建立红黑树结构,等等
红黑树的性质:
1.节点不是红色的就是黑色的。
2.根节点是黑色的
3.如果一个节点是红色的,那么他们的孩子都必须是红色的(这一条性质也说明这个节点的父节点肯定是黑色,不会存在两个相邻的红色节点)
4.对于每个节点到其叶子节点的黑色节点的数量是相同的
C语言的实现:
1.涉及到的数据结构:
typedef struct _node {
int color; //代表节点的颜色1表示黑色节点,0表示红色节点
struct _node *parent;
struct _node *left;
struct _node *right;
int value; //代表节点的值
} node;
2.节点操作:
节点的后继节点(节点删除时会用到)
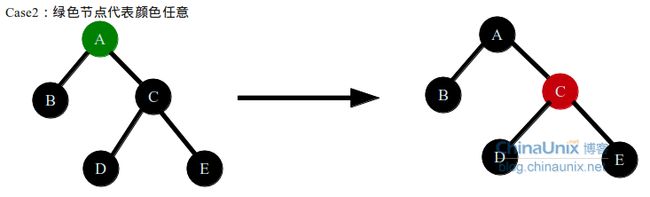
红黑树的节点的插入过程,和普通的二叉查找树的插入过程类似。只是每个节点多了一个color域,代表节点的颜色(红色,黑色),新插入的节点的颜色是红色的。每个节点插入之后需要看一下当前插入节点的parent节点是否为红色,如果为黑色,则2叉树继续保持红黑树性质3,4,如果为红色,破坏了红黑树性质3,这时需要调整一下节点节点的颜色。所以当插入节点的父节点为红色时,插入后的节点调整需要分为3个case:
case1:第一种情况的条件是uncle节点不为空,并且uncle节点为红色节点。target节点是parent节点的左孩子或者右孩子,插入target节点之前,会保证数据结构中没有相邻的红色节点,且到叶子节点的黑色数目相同,这时插入target节点,只需要把parent节点,uncle节点变成黑色,grand节点变为红色即可,这样把grand节点的黑色下降到了孩子节点上(parent,uncle),保持了没有相邻的红色节点,且到叶子节点黑色数目相同,但是这样把grand节点变成了红色,可能会影响grand的父节点的红黑树性质(如果grand->parent节点为红色),所以需要把target节点变成grand节点,递归grand节点之上的数据结构。
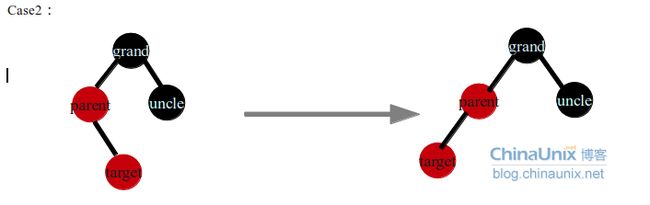
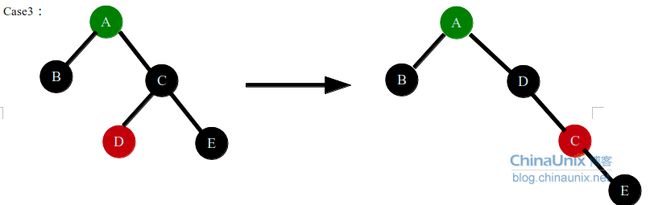
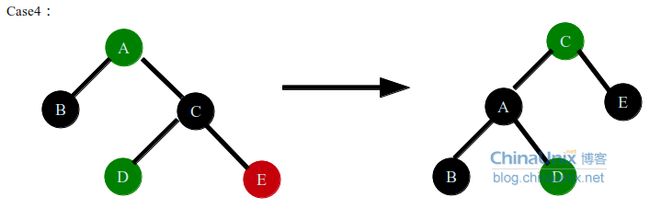
case2是个过渡阶段,目的是让target节点为parent节点的左孩子,这样在后面的右旋时,target节点才不会成为grand的左孩子,正确的做法是交换target和parent节点,然后左旋target节点,进入case3,结果如右图。反之如果在case2中直接右旋grand节点,(目的是保持没有相邻的红色节点,同时黑色节点数量保持一致)会出现下面几种情况(列举几个都不是不可取的):
第一种情况错误的旋转,交换parent节点和grand结果的颜色,显然这样的结果违反了不能出现两个连续的红色节点的性质
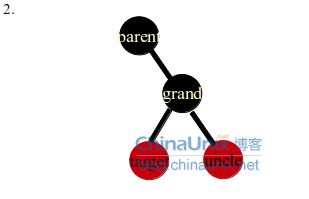
第二种情况错误的旋转,交换uncle节点和parent节点的颜色,同时uncle节点为红色,这样会导致uncle左右子树可能出现连续两个红色节点,剩下的错误旋转情况都是显而易见的,不是黑色节点的个数多了就是违反了红色节点不能相邻。
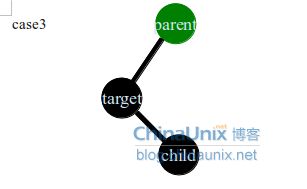
case3情况是插入的target节点是parent节点左孩子,或是右孩子通过case2的操作变成了左孩子,这种情况直接右旋grand节点,并且交换parent节点和grand节点的颜色即可,这种情况不用在递归parent节点的上层数据结构了因为从grand节点的父节点看到的子节点就是黑色的,case3转换完毕后子节点还是黑色的,并且左右子树黑节点的数量维持不变,所以这种情况不用递归父节点的数据结构了。
插入过程的最后需要将root节点置为黑色,这是因为,case1中有可能grand节点就是root节点,case1的最后将root置为了红色,这时root节点没有父节点了,需要保持红黑树的性质,将root节点置为黑色。
普通二叉树节点删除过程:
普通二叉数节点删除过程分为2种情况(删除target节点):
case1这种情况就是target节点只有一个孩子,无论只有左孩子,还是只有右孩子,在这种情况下删除target节点,这种情况比较简单,就是直接删除target节点,然后重新把parent节点和child节点的父子关系设置好即可
case2中,需要删除的节点target,即有左孩子,又有右孩子,所以按照case1的做法不可取,两个节点不能同时作为parent节点的子节点,所以这时需要寻找一个节点代替target节点,显而易见,这个节点要比parent节点要大,所以结果应该在parent的右子树数中,也就是target节点的左右子树中,同时还有满足两个条件中的任意一个:
1.这个节点的值要要等于c2节点子树的最小值
2.这个节点的值要要等于c1节点子树的最大值
所以这时候可以选择c2子树中最小的replace节点,或者为c1右孩子中最大的那个节点。
这时找到了这个节点,同时这个节点肯定只有一个孩子,如果是target节点的右孩子中的最小值,那么这个最小值节点肯定是没有左孩子的;如果这个节点是target节点中的左孩子中的最大值,那么这个最大值节点是肯定没有右孩子的。找到了这个代替的节点replace节点之后,需要把这个节点删除掉,同时把replace节点的值和target节点的值做个交换,这样target节点就这样间接的删除了
红黑树删除节点后的影响:
第一种情况删除target节点之后,没有任何影响,直接删除,因为target节点是红色的删除不会影响节点到叶子节点黑色节点的数量,同时parent节点和child节点肯定都是黑色的,也不会影响到parent节点和child节点连接导致红色节点相邻。
第二种情况parent节点的颜色任意,但是target节点为黑色,同时child节点为红色,这种情况下删除target节点后,只需要将child节点染为黑色,就可弥补target节点的删除导致的parent左孩子黑色节点少1的情况,同时child的变黑也不影响parent节点的颜色(parent节点颜色可以为红色也可以为黑色)。
第三种情况target节点为黑色,child节点为黑色,这时删除了target节点,很明显parent左子树少了一个黑色节点,不满足红黑树的性质(到任何叶子节点黑色节点数量相同),这时需要协调一下parent右子树和左子树结构,使得黑色节点数量重新平衡一致,而且不出现相邻的红色节点。
红黑树节点调整分为4种情况,情况如图case1中,在A节点和B节点中间原来存在被删除的节点,这个节点颜色是黑色的,删除这个节点会导致B节点的左子树黑色节点数量少1,同时单单调整B的左子树的节点颜色是不能保持红黑树性质。这时需要整体调整一下B节点左右子树的结构,B节点左子树黑色节点数量少1,可以采取的方法不外乎两种:
1.在B左子树黑色节点数量不变的情况下,调整B右子树黑色节点数量少1,这种方法需要递归B节点的父节点及其以上的数据结构
2.我们会发现在B左子树的结构中,让左子树的黑色节点数量增加一个已经是不可能,所以可以通过左旋转B节点,让左子树的节点多一个,这样就有机会将这个节点置为黑色,重新保持红黑色性质
节点调整会分为4种情况

case1这种情况,当前的情况是B节点的左子树黑色节点数量少1,右子树有红色节点,如果采用方法1不可能,D节点已经为红色,无论更改C,E节点的颜色都会破坏红黑树性质(无相邻红色节点),只能采取第二种做法,左旋B节点,同时将D节点(叔父节点)变为黑色,B节点变为红色,这样保持红黑树的性质,D节点的右子树黑色节点数目2个,同时左子树中DBC分支中黑色节点数目也是2个,现在问题变为了B节点的左子树黑色节点的数目和右子树黑色节点数目相同,然后进入case2
case2中,A节点和B节点之间删除了黑色节点,使得A节点的左子树黑色节点数量少1,A节点的颜色可以任意,这时盲目改变A节点的颜色不可取。这时可以采用方法1,就是使得A节点右子树黑色节点数量少一个,可以改变C节点(叔父节点)的颜色,变为红色,不可将DE节点全都变为红色,这样会影响DE的子节点,如果他们的子节点中右红色的,这样会违反红黑树性质(不能有相邻的红色节点)。这样A节点变为黑色,C节点变为红色,这样A节点左右子树黑色节点数目相同了,但是对于A节点的父节点,认为A这一子树整体黑色节点数目少了一个,所以这种情况需要递归A的父节点结构。
case3中,这种情况下,如果用解决方法1,就是让A节点右子树中黑色节点数量少一个,这样只能更新C节点的颜色为红色,这样D节点也为红色,CD节点为相邻的红色节点,违反了红黑树的性质。如果用解决方法2,让A节点的左子树黑色节点数量增加1个,如果不管A节点颜色,强行将A节点的颜色变为黑色,不但没有平衡,A的右子树黑色节点也会加1.所以只能左旋节点A,然后在根据情况重新对节点着色,试想,目标就是让A节点位置的节点的左子树黑色节点数量增加1个,左子树黑色节点数量不变,可以肯定的是A节点肯定要变为黑色,所以不用管D节点的颜色,这时如果E节点为黑色,这样导致了旋转过后C节点右子树的黑色节点数量加1,强行更新E节点的颜色为红色,又会导致它的子节点破坏红黑树性质,如果C节点的右子树为红色,就好办了,所以这时需要先右旋C,使得D位置节点的右孩子为红色。右旋C节点,C节点变为红色,D节点变为黑色,这样旋转完毕后,D节点的左右孩子继续保持红黑树性质,然后进入case4
case4中在A节点颜色任意,B节点为黑色,AB节点之间删除了一个黑色节点后,需要调整下数据结构,只需要A节点和C节点交换颜色即可,如图C节点的右子树的黑色节点数量不变,同时左子树结构多了一个黑色节点,弥补了删除的黑色节点。其中D节点颜色我们是不关心的,因为在A节点左旋后,D节点会成为A节点的右孩子,A节点会变为黑色,所以D节点颜色任意。
29.分裂树/伸展树/Splay Tree-平衡二叉查找树
http://www.cnblogs.com/vamei/archive/2013/03/24/2976545.html
http://www.cnblogs.com/huangxincheng/archive/2012/08/04/2623455.html
我们讨论过,树的搜索效率与树的深度有关。二叉搜索树的深度可能为n,这种情况下,每次搜索的复杂度为n的量级。AVL树通过动态平衡树的深度,单次搜索的复杂度为log(n) (以上参考纸上谈兵 AVL树)。我们下面看伸展树(splay tree),它对于m次连续搜索操作有很好的效率。
伸展树会在一次搜索后,对树进行一些特殊的操作。这些操作的理念与AVL树有些类似,即通过旋转,来改变树节点的分布,并减小树的深度。但伸展树并没有AVL的平衡要求,任意节点的左右子树可以相差任意深度。与二叉搜索树类似,伸展树的单次搜索也可能需要n次操作。但伸展树可以保证,m次的连续搜索操作的复杂度为mlog(n)的量级,而不是mn量级。
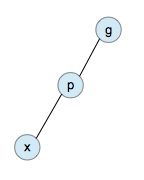
具体来说,在查询到目标节点后,伸展树会不断进行下面三种操作中的一个,直到目标节点成为根节点 (注意,祖父节点是指父节点的父节点)
1. zig: 当目标节点是根节点的左子节点或右子节点时,进行一次单旋转,将目标节点调整到根节点的位置。
zig
2. zig-zag: 当目标节点、父节点和祖父节点成"zig-zag"构型时,进行一次双旋转,将目标节点调整到祖父节点的位置。
zig-zag
3. zig-zig:当目标节点、父节点和祖父节点成"zig-zig"构型时,进行一次zig-zig操作,将目标节点调整到祖父节点的位置。
zig-zig
单旋转操作和双旋转操作见AVL树。下面是zig-zig操作的示意图:
zig-zig operation
在伸展树中,zig-zig操作(基本上)取代了AVL树中的单旋转。通常来说,如果上面的树是失衡的,那么A、B子树很可能深度比较大。相对于单旋转(想一下单旋转的效果),zig-zig可以将A、B子树放在比较高的位置,从而减小树总的深度。
下面我们用一个具体的例子示范。我们将从树中搜索节点2:
Original
zig-zag (double rotation)
zig-zig
zig (single rotation at root)
上面的第一次查询需要n次操作。然而经过一次查询后,2节点成为了根节点,树的深度大减小。整体上看,树的大部分节点深度都减小。此后对各个节点的查询将更有效率。
伸展树的另一个好处是将最近搜索的节点放在最容易搜索的根节点的位置。在许多应用环境中,比如网络应用中,某些固定内容会被大量重复访问(比如江南style的MV)。伸展树可以让这种重复搜索以很高的效率完成。
30.B树、B+树、B*树
B-树即B树
B树
是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
如:(M=3)
B树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果
命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为
空,或已经是叶子结点;
B树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其最底搜索性能为:
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;
所以B树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占
M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;
B+树
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
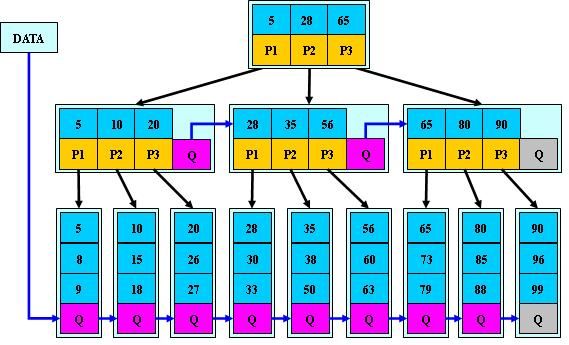
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
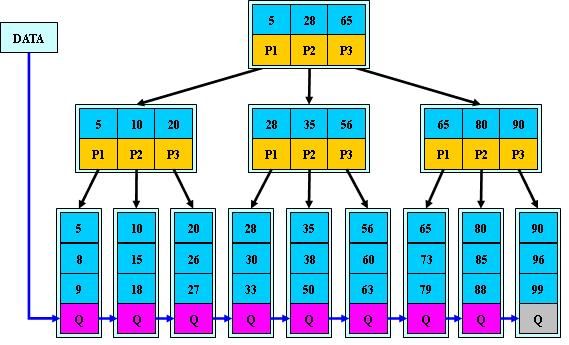
如:(M=3)
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在
非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统;
B*树
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3
(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据
复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父
结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分
数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字
(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之
间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
小结
B树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键
字范围的子结点;
所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;
B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点
中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;
B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率
从1/2提高到2/3;