AVR121-使用过采样增加ADC精度
1. 介绍
在大多数情况10位精度已经足够了,但是某些情况下需要更高的精度。特殊的信号处理技术可以用来提高测量的精度。使用一种称为“过采样和抽取”的方法可以得到较高的精度,不需要使用外部的ADC。
Figure 1-1. 增加分辨率
2. 操作理论
ADC的参考电压和ADC的精度决定了ADC的步距。ADC的参考电压VREF可以选择使用AVCC,内部的2.56V / 1.1V参考电压,或者AREF引脚上的电压。较低的VREF提供了较高的电压精度但是同时减少了输入信号的动态范围。如果2.56V的VREF被选择,它将给用户大约2.5mV的转换精度,并且最高的输入电压是2.56V。选择使用ADC输入通道的增益,这使用户有更好的精度来测量模拟信号,代价是损失ADC的动态范围。如果不能接受以动态范围交换精度,可以采用过采样来增加精度。这个方法受到ADC的特性限制:使用过采样和抽取将降低ADC的量化误差,但是不能减少ADC的非线性化误差。
2.1 采样频率
Nyquist定理规定信号的采样频率必需至少是信号频率的两倍,否则高频部分将有损失(带通)。最小需要的采样频率称为Nyquist 频率。
公式 2-1. Nyquist 频率
这里 fsignal 是输入信号的最高频率,上面的采样频率 fnyquist 称为过采样。这个采样频率只是理论上的绝对最小频率,在实际中,用户通常希望尽可能高的采样频率,在时域中获得最好的效果。这样有人可能会说在大多数情况下输入信号已经是过采样了。
采样频率是CPU时钟的分频的结果,一个较低的分频系数给出较高的ADC时钟频率。在一个特定点,较高的ADC时钟将降低转换的精度,即有效数据位ENOB(Effective Number Of Bits)。 所有的ADC都有带宽限制, AVR的ADC也不例外,按照数据手册的说法,要获得10位转换精度,ADC时钟频率大概在50kHz –200kHz。当ADC时钟是200kHz时,采样频率大约是15kSPS(次每秒),可以采样信号的上限大约是~7.5kHz。按照数据手册,ADC时钟最高可以到1Mhz,
尽管这将降低ENOB。
3. 理论
3.1 过采样和抽取
过采样和抽取理论的背后是非常复杂的,但是的方法却是比较容易的。这个技术要求大量的采样,这些额外的采样完成信号过采样。每增加额外的一位精度,信号必需过采样4倍。频率和输入信号的关系在公式3-1中。为了尽可能最好的重现信号,这么多次的采样是必需的,因为大量的采样平均后可以更好的重现输入信号。这可以认为是这篇应用笔记的主要内容,下面的理论和例子用来进一步解释。
公式 3-1. 过采样频率
3.2 噪声
为了使这个方法正常工作,信号成分在转换过程中不能发生变化。但是成功增加精度的另一个标准是输入信号在采样时有所变化。这看起来是矛盾的,因为信号的变化意味着较少有效的 LSB,变化的信号可以看成是信号的噪声成分。在信号过采样时,噪声使信号产生微小的变化。ADC的量化误差一般至少是0.5LSB,因此噪声幅度超过0.5 LSB就改变了LSB。噪声幅度有1-2LSB时更好,因为可以保证几次采样不会总是相同的值。
使用抽取技术时,噪声的标准:
- 信号成分在转换时不能变化。
- 信号上有一定的噪声。
- 噪声的幅度至少有1 LSB。
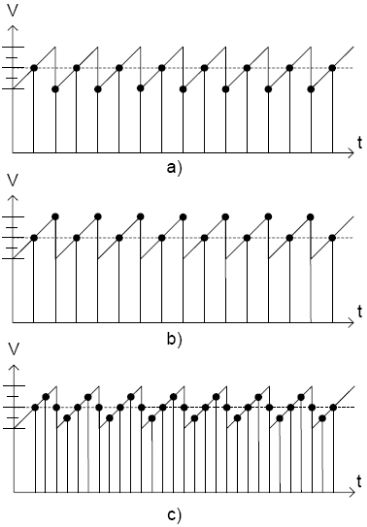
通常AD转换时有一定的噪声,噪声可能是热噪声、CPU的核心产生的噪声、I/O端口切换带来的噪声、电源变化引起的噪声(特别是开关电源)等等。这些噪声在大多数情况下可以使这个方法正常工作了,但是在特殊情况下,需要引入噪声到输入信号,这个方法叫抖动。图 3-1 (a)展示了测量电压信号的在两档之间时,简单将4次采样结果平均没有太大作用,结果可能是同样的数字,它只能消除信号的波动。图3-1 (b) 显示添加人工噪声到输入信号后,改变了转换结果的LSB。添加4次采样同样的采样步骤,产生的结果给出更好的精度,如图3-1 (c) 所示,ADC的“虚拟精度”从10位增加到11位。这个方法就是抽取,在3-3小节会进一步讲解。
图 3-1. 精度从10位增加11位

另外使用这个方法的理由是可以增加信噪比,提高有效位数ENOB,并将噪声平展开来,使噪声对每个二进制数的影响减少。双倍的采样频率将减少带内噪声3dB,增加有效测量精度0.5位。
3.3 平均
一般平均就是采样M次,结果之和再除以M。正常平均时,ADC测量的数据等效于通过了一个低通滤波器,减弱了信号的波动噪声,并使峰值平缓。滑动平均法经常用来这样做,读取M次,将结果放到一个循环队列,平均最近M次的结果。它有轻微的延时,因为每次的结果都是最后M次采样的结果。数据窗口可以重叠也可以不重叠,图 3.2 显示了 7个(Av1-Av7) 独立的不重叠滑动平均的结果。
要注意普通平均不会增加转换的精度,抽样或插值方法和过采样一起使用,才能增加精度。数字信号处理过采样和信号低通滤波经常看成是插值。这时,插值用来产生在大量采样后的新采样结果。越多的平均采样数,越容易选择低通滤波,插值结果越好。额外的M次采样,象普通平均那样累加起来,但是结果不象普通平均那样除以M。而是结果右移N(N是希望增加的额外精度),从而比例化成正确的结果。右移一个二进制数一次等于除以2。如公式3-1,精度从10位增加到12位需要总共16次10位的采样。这16次10位结果产生一个14位计算结果,其中最后两位是无用的,右移后成为12位结果。比例系数sf在公式3-2给出,它是总共4n次采样后的除数,这样才能得到正确的比例化结果。n是需要的额外精度。
公式 3-2.
3.4 过采样和抽取什么时候工作
正常情况下信号包含了一定的噪声,这个噪声通常具有高斯噪声的特性,更常用的名称是白噪声或热噪声,在宽频谱中总能量均匀分布在整个频段范围。在这些情况下,如果噪声的幅度可以改变ADC的LSB,‘过采样和抽取’的方法就能够工作。
在其他情况,就有必要引入人工的噪声到输入信号中,这个方法叫做抖动。这个噪声波形应当是高斯噪声,不过周期性的噪声也可以。噪声信号的频率和采样频率有关,一个原则是:“当添加N次采样时,噪声周期不能超过N次采样的周期”。噪声的幅度至少需要1LSB。.当添加人工噪声时,需要记住噪声的值是0;不充分的过采样会产生偏差,如图3-3.
虚线是锯齿波信号的平均值,图3-3 (a)将引起负偏差,图3-3 (b) 引起正偏差,图3-3(c)的采样是充分的,就避免了偏差。为了产生人工噪声信号,可以使用AVR单片机的计数器。因为计数器和ADC使用了相同的时钟源,这就能使噪声和采样频率同步,避免了偏差。
3.5 例子1
一个都柏林的酿酒师想测量酿酒时的温度。一个缓慢变化的信号表示了温度,在这种环境下一 般温度对应的电压是2.5 V。图3-4显示了温度测量设备的特性。
酿酒师不希望缩小输入信号的范围,选择5V作为ADC的基准。这时10位ADC不能提供足够精度的转换结果,因为结果的LSB大约是5mV的‘步距’。这个结果会引起0.25°C的误差,所以不能被接受。酿酒师希望结果有0.1°C的精度,要求电压的分辨率小于2mV。如果测量使用了12位的ADC,那么电压步距的LSB将减小到约1.22mV。酿酒师需要的是用10位ADC产生虚拟12位ADC结果。输入信号是缓慢变化的,不需要很高的采样频率。按照数据手册,ADC时钟频率在50kHz到200kHz之间可以保证10位精度,酿酒师因此选择了50kHz的ADC时钟频率。采样频率变为约3800次/秒。一个温度下测量出直流参数是2.4729V,表 3-1 显示了不同分辨率选项下测量的这个参数,Vin = 2.4729V 而 VREF = 5V。
Table 3-1. 分辨率选项
| 分辨率 | 电压分辨率 | 过采样 | 右移 | 理想抽取结果 | 理想电压 | 最大带宽 |
|---|---|---|---|---|---|---|
| 10 | ~5 mV | NA | NA | NA | 2.4658V | ~7600Hz |
| 11 | ~2.5 mV | 4X | 1X | 1012 | 2.4707V | ~1900Hz |
| 12 | ~1.22mV | 16X | 2X | 2025 | 2.4719V | ~475Hz |
| 13 | ~610 uV | 64X | 3X | 4051 | 2.4725V | ~118Hz |
| 14 | ~300 uV | 256X | 4X | 8103 | 2.4728V | ~29Hz |
| 15 | ~150 uV | 1024X | 5X | 16206 | 2.4728V | ~7Hz |
| 16 | ~75 uV | 4096X | 6X | 32413 | 2.4729V | ~3Hz |
注:1. ADC 时钟 = 200kHz
这个结果单次转换结果是505,初略看上去结果是正确的,但是这个二进制数字相当于2.4683V, 这使用户不确定温度测量的误差,在某些情况下可能是危险的。如前面推断的,信号通常包含了足够的噪声来使用抽取法。
为了增加1位精度,添加4次相邻的采样,这些采样出的值相互之间因为有噪声存在所以有微小的不同。添加4次采样:508 + 507 + 505 + 505 = 2025。按照抽取原则,增加n位精度,就需要右移n次。结果右移1位,最后移位后结果是1012。同样,信号充分过采样可以进一步提高精度, 达到12位。添加16次10位采样并右移2位结果就能达到,结果是2025。这个数字更可信,因为使用12位结果时误差已经减少到约1.22mV。这个例子显示了用户起初采样一个缓慢变化信号, 采样速度是3800次每秒,电压精度约5mV。现在采样速度是240次每秒,12位精度,电压精度 约1.22mV。
用户可以按惯例平均16次12位采样结果以消除波动,这就是把16次采样结果加起来在除以16,最终用户得到的是15 SPS 的12位采样。(15 * 16 * 16 = 3840)
- 普通平均将减少随机噪声
- 过采样和抽取将利用噪声增加精度
3.6 例子2
为了展示这个方法,下面的例子将显示怎样不需要使用外部的ADC获取更高的精度。一个信号发生器用来产生0V到5V的线性斜坡信号。在一个‘低噪声’环境下,一个信号发生器和一个AVR单片机连接到STK500开发板,这可能没有足够大的噪声来影响10位的信号。这就需要引入人工噪声信号到输入的信号。有4种方法被成功使用:
- 添加信号发生器产生的噪声,直接连到输入信号。
- 使用AVR的PWM产生噪声。
- 当使用AVCC作为VREF时,使用AVR产生的噪声添加到AREF。
- 当使用AREF作为VREF时,添加AVR产生的噪声到AREF。
最容易的方法是直接添加白噪声到信号,但在大多数情况用户没有或者不希望有这种噪声。一个更可行的方法是使用AVR单片机产生一个PWM信号,然后低通滤波这个‘噪声’成直流,并且纹波的峰值达到LSB,一个这样的例子在图 3-5中展示。
图3-5. LP-滤波
如果VCC = 5V,滤波的信号在 AREF 引脚有2.5V,当计数器的占空比是0%时;当占空比是100%就是5V。在这个例子,占空比是50%,基本频率大约是3900Hz,10kΩ的电位器用来调节纹波。PWM信号即作为ADC的参考电压,也作为噪声发生器(AVCC作为ADC的参考电压)。这个方法认为参考电压的微小变化和输入信号的微小变化结果是相同的,这就不用干扰输入信号了。
图 3-6显示测量线性斜坡信号。图3-7显示10位离散化的输入斜坡信号,测量没有添加人工噪声, 量化步距是很明显的。为了增加精度,就要减少量化步距。
图3-7. 10位精度量化的信号
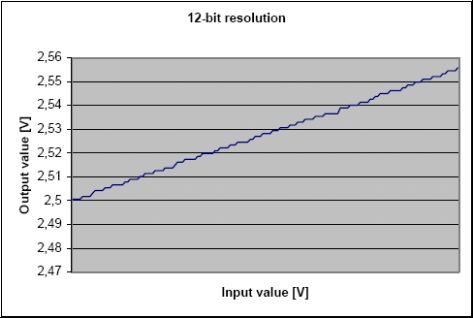
图3-8显示出输入信号12位离散化结果(AREF作为ADC的参考电压,AREF添加了噪声)。按照 公式3-1,每12位结果需要16次10位采样。ADC偏差调整和应用笔记AVR120一致,增益误差也需要调整。
图3-9显示14位离散化结果,图3-10显示16位的结果。当测量信号包含噪声,或者参考电压象这个例子的,要注意顶端和底端的值要减去噪声信号的幅度,稍微减少了测量信号的动态范围。在某些情况下,作为安全边界,偏差是100mV。
图3-9. 14位精度量化的信号
你可以清楚地看到过采样和抽取法显著增加了精度。
总结
当ADC采样一个信号时,不连续的量化信号会引入一些误差,通常称为量化误差。一般平均的只能消除信号的波动,但抽取法可以提高精度。对一个4倍过采样的信号,4个相邻的数据点平均产生一个新的数据点。过采样频率的计算参考公式3-1。添加额外的采样并右移结果系数n,产生提高n位精度的结果。平均4次ADC采样的结果获得新ADC的结果是同样ADC采样速率的¼,但是同时平均了量化噪声,改善了SNR,这将增加ENOB并减少量化误差。快速的ADC和低内存消耗,使得过采样的优点是显著的。
- 增加一些噪声到信号,至少 1 LSB。
- 如果噪声的幅度不够,添加噪声到信号。
- 累计 4n 次10位采样,这里 n 是希望得到的额外精度。
- 右移n次,比例累计的结果。
- 按照应用笔记AVR120补偿误差。
参考资料
- 用过采样和求均值提高ADC分辨率
- AVR121:使用过采样增加ADC精度
- 过采样技术提高 ADC 分辨率