poj 1845 Sumdiv(二分递归求等比数列+素因子分解)
题目:http://poj.org/problem?id=1845
Sumdiv
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 16348 | Accepted: 4075 |
Description
Consider two natural numbers A and B. Let S be the sum of all natural divisors of A^B. Determine S modulo 9901 (the rest of the division of S by 9901).
Input
The only line contains the two natural numbers A and B, (0 <= A,B <= 50000000)separated by blanks.
Output
The only line of the output will contain S modulo 9901.
Sample Input
2 3
Sample Output
15
Hint
2^3 = 8.
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
分析:大意是让我们求A^B的所有因子的和。假设A=180=2^2*3^2*5,B=2,那么A^B=(2^2*3^2*5)^2=2^4*3^4*5^2,它所对应的因子和是(1+2+……+2^4)*(1+3+……+3^4)(1+5+5^2)。做到这一步时我原来的思路是直接套用等比公式再乘法逆元的方法做。然而,出错了,真不知道问题在哪里。。提一句,关于等比公式:
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
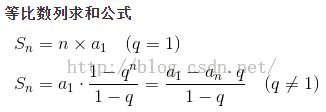
关于费马小定理的降幂:
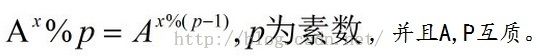
为下面的代码默哀3分钟:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int mod=9901; //mod是一个质数--》乘法逆元
typedef long long LL;
LL factor[7500][2], sum; //factor的一维长度不要太大,否则会MLE
void resolve(LL x){
sum=0;
memset(factor,0,sizeof(factor));
for(int i=2;i*i<=x;i++){
if(x%i==0){
factor[sum][0]=i;
while(x%i==0){
factor[sum][1]++;
x/=i;
}
sum++;
}
}
if(x>1){
factor[sum][0]=x;
factor[sum++][1]=1;
}
}
LL quick_mod(LL a,LL b){
LL ans=1,temp=a%mod;
while(b){
if(b&1) ans=ans*temp%mod;
temp=temp*temp%mod;
b>>=1;
}
return ans;
}
LL Extend_Eulid(LL b,LL a) //逆元 d mod
{
LL x1,x2,x3,y1,y2,y3 ;
x1=1,x2=0,x3=a,y1=0,y2=1,y3=b ;
while(y3 && y3!=1)
{
LL q=x3/y3 ;
LL t1,t2,t3 ;
t1=x1-q*y1,t2=x2-q*y2,t3=x3-q*y3 ;
x1=y1,x2=y2,x3=y3 ;
y1=t1,y2=t2,y3=t3 ;
}
if(!y3)return -1 ;
while(y2<0) y2+=mod; // 保证是非负数
return y2 ;
}
int main()
{
//freopen("cin.txt","r",stdin);
LL a,b;
while(cin>>a>>b){
if(b==0){ puts("1"); continue; }
if(a==0){ puts("0"); continue; }
resolve(a);
LL ans=1;
for(LL i=0;i<sum;i++){
factor[i][1]*=b;
factor[i][1]++;
LL pow=factor[i][1]; //%(mod-1);
LL m=(quick_mod(factor[i][0],pow)-1+mod)%mod;
LL ni=Extend_Eulid(factor[i][0]-1,mod);
ans=(ans*m%mod)*ni%mod;
}
printf("%lld\n",ans);
}
return 0;
}
我看了别人都是二分递归求等比数列的。好吧,用这种方法。思路:等比数列求和,递归二分:对于1+p+p^2+……+p^n,如果n是一个奇数,那么这里有偶数项:比如n=5:S=1+p+p^2+p^3+p^4+p^5=(1+p)+p^2(1+p+p^2+p^3) n=3: S=1+p+p^2+p^3=(1+p)+p^2(1+p);
于是得到:1+p+p^2+p^3+........+p^n=(1+p+p^2+....+p^(n/2))*(1+p^(n/2+1));
如果n是一个偶数,那么这里有奇数项,比如n=4:S=1+p+p^2+p^3+p^4=(1+p)+p^2+p^3(1+p)=(1+p)(1+p^2+p^3) n=2: S=1+p+p^2
于是得到:1+p+p^2+p^3+........+p^n=(1+p+p^2+....+p^(n/2-1))*(1+p^(n/2+1))+p^(n/2);
memory:836KB,time:16ms
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int mod=9901;
typedef long long LL;
LL factor[7500][2], sum;
void resolve(LL x){
sum=0;
memset(factor,0,sizeof(factor));
for(int i=2;i*i<=x;i++){
if(x%i==0){
factor[sum][0]=i;
while(x%i==0){
factor[sum][1]++;
x/=i;
}
sum++;
}
}
if(x>1){
factor[sum][0]=x;
factor[sum++][1]=1;
}
}
LL power(LL a,LL b){
LL ans=1,temp=a%mod;
while(b){
if(b&1) ans=ans*temp%mod;
temp=temp*temp%mod;
b>>=1;
}
return ans;
}
LL cal(int p,int n){
if(n==0) return 1;
if(n&1){//(1+p+p^2+....+p^(n/2))*(1+p^(n/2+1));
return (1+power(p,n/2+1))*cal(p,n/2)%mod;
}
else { //(1+p+p^2+....+p^(n/2-1))*(1+p^(n/2+1))+p^(n/2);
return (power(p,n/2)+(1+power(p,n/2+1))*cal(p,n/2-1))%mod;
}
}
int main()
{
//freopen("cin.txt","r",stdin);
LL a,b;
while(cin>>a>>b){
if(b==0){ puts("1"); continue; } //0^0=1
if(a==0){ puts("0"); continue; }
resolve(a);
LL ans=1;
for(LL i=0;i<sum;i++){
factor[i][1]*=b;
ans=ans*cal(factor[i][0],factor[i][1])%mod;
}
printf("%lld\n",ans);
}
return 0;
}