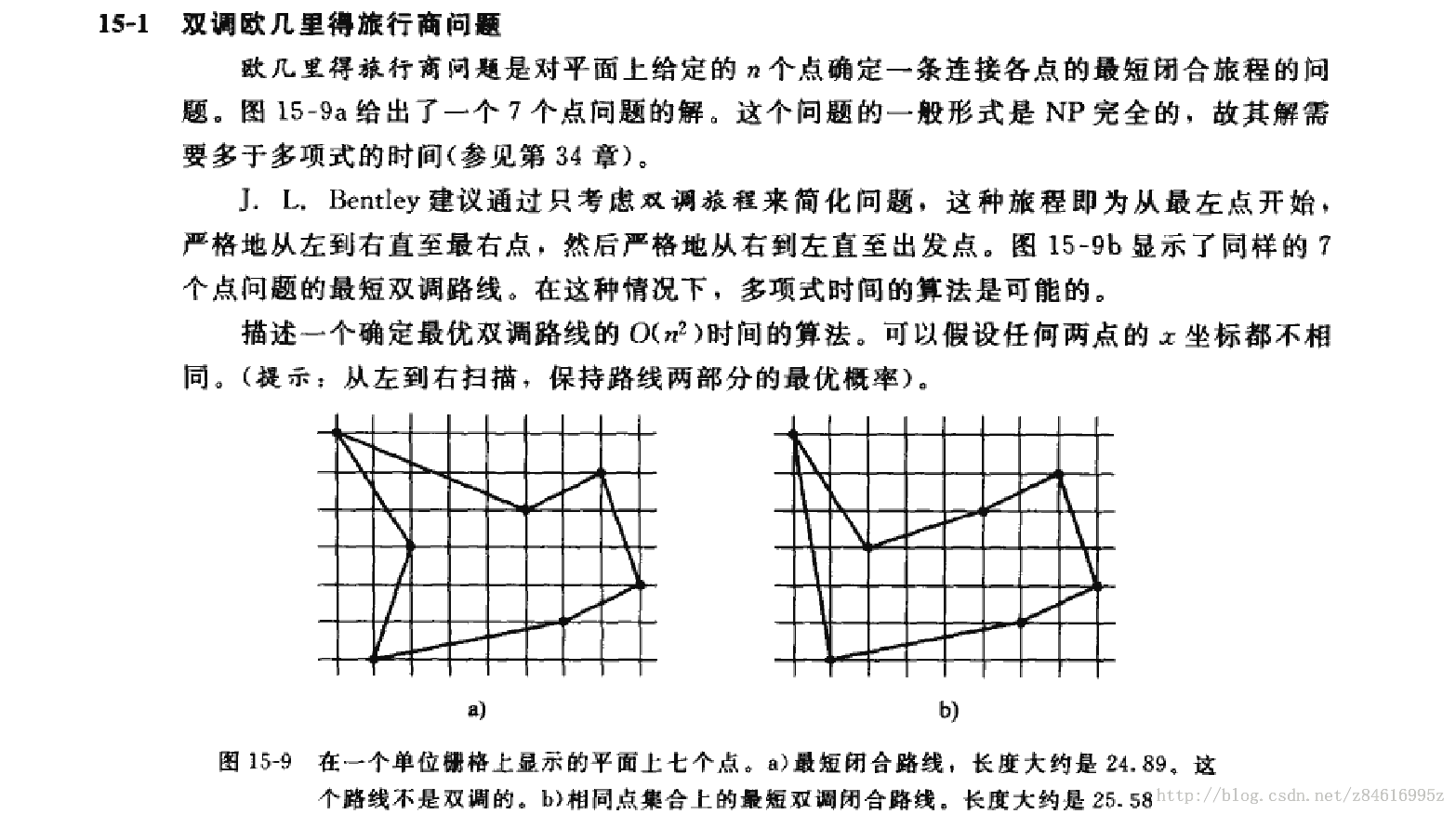
动态规划之双调欧几里得旅行商问题

解题思路：①首先把横坐标x排序，大约用时O(nlgn),用堆排序或者归并排序都能达到此效果。提示既然是从左到右扫描，那么x坐标从左到右是按照递增顺序扫描。

                  ②子结构：在按照①已排好序的基础上，才能进行这步操作，注意排序过程这里已省略。下面定义b[i][j]=从左边第1个点到第i个点的距离+从左边第1个点到第j个点的距离，并且两条路径上必须经过各不相同的所有1到i到j之间所有点。用distance(T,i,j)=|pipj|表示从第i个点到第j个点的直线距离。

                  ③归纳的递归公式如下：

代码如下：

#include <iostream>
#include <math.h>
using namespace std;
#define n 7
struct Coordinate
{
	double x;double y;
}T[n];
//计算点i和点j之间的直线距离  
double distance(Coordinate T[],int i,int j)  
{  
    return sqrt((T[i].x - T[j].x) * (T[i].x - T[j].x) +  (T[i].y - T[j].y) * (T[i].y - T[j].y));  
} 
double Bitonic_euclidean_traveling_salesman_problem(struct Coordinate T[])
{//双调欧几里得旅行商问题
	double b[n+1][n+1]={0};//记录最短路径的长度 
	//计算所有情况下的b[i][j]，1 <= i <= j  
	b[1][2] = distance(T,1,2);//初始化  
    for ( int j=3;j<=n;j++)
    {
	   //i < j-1  
       for (int i=1;i<=j-2;i++)
       {
		   b[i][j]=b[i][j-1]+distance(T,j-1,j);
       }
	   //i = j - 1,b[i][j] = min(b[k][j - 1] + distance(k,j)); 
	   b[j-1][j]=0x7fffffff;
	   for (int k=1;k<=j-2;k++)
	   {
		   double q=b[k][j-1]+distance(T,k,j);
		   if (q<b[j-1][j])
		   {
			   b[j-1][j]=q;
		   }
	   }
    }
	b[n][n]=b[n-1][n]+distance(T,n-1,n);
	return b[n][n];
}
void main()
{  
	struct Coordinate T[n+1]={0};
    for( int i = 1; i <=n; i++) 
        cin>>T[i].x>>T[i].y; 
	cout<<Bitonic_euclidean_traveling_salesman_problem(T)<<endl;
}

样例输出：

总结：此程序运行时间为O(n²)，这里的难点主要在归纳递推公式上(i<j-1与i=j-1两种情况需要反复思考才可能得出结论)，其次才是具体实现。