Neural Turing Machines-NTM系列（三）ntm-lasagne源码分析

Neural Turing Machines-NTM系列（三）ntm-lasagne源码分析

在NTM系列文章（二）中，我们已经成功运行了一个ntm工程的源代码。在这一章中，将对它的源码实现进行分析。

1.网络结构

1.1 模块结构图

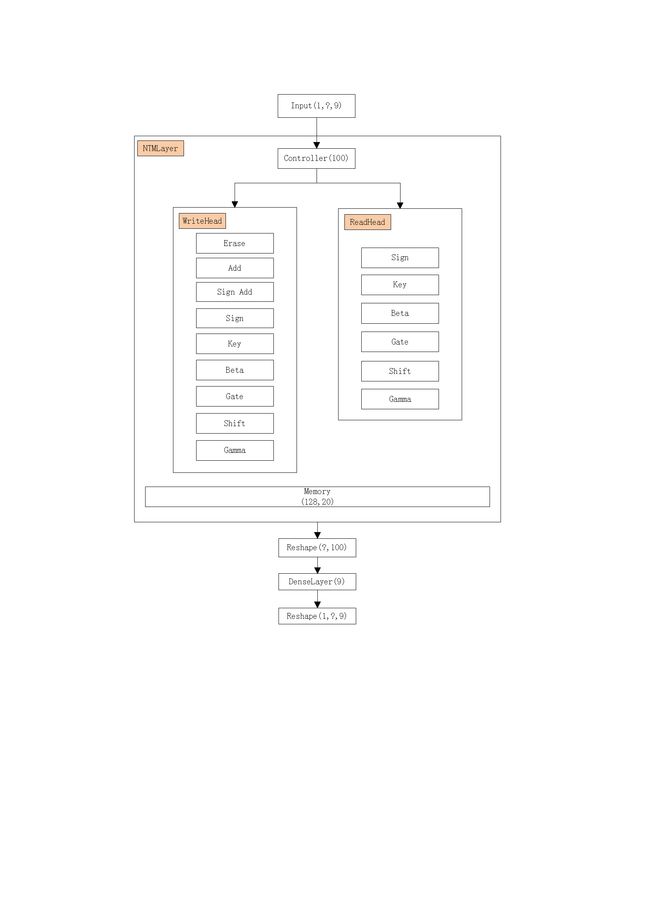
在图中可以看到，输入的数据在经过NTM的处理之后，输出经过NTM操作后的，跟之前大小相同的数据块。来看下CopyTask的完整输出图：

图中右侧的Input是输入数据，Output是目标数据，Prediction是通过NTM网络预测出来的输出数据，可以看出预测数据与目标数据只在区域上大致相同，具体到每个白色的块差距较大。（这里只迭代训练了100次）
训练次数可以在这里调整（task-copy.py）：

其中的参数max_iter就是训练时的迭代次数，size是输入的数据宽度（即上图中Input/Output小矩形的“高”-1，多出来的维度用作结束标记）
输入数据如下，从上到下对应上图中的从左到右，最后一行是结束标志，只有最后一个元素为1：
array( [[
[ 0., 1., 1., 0., 1., 1., 1., 1., 0.],
[ 0., 1., 1., 0., 0., 1., 0., 0., 0.],
[ 0., 0., 1., 0., 1., 1., 1., 0., 0.],
[ 1., 1., 1., 1., 1., 1., 1., 0., 0.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 1.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0, 0., 0., 0., 0.],
]]
目标数据和预测数据的格式相似，就不详细介绍了。需要注意的是，由于输出层使用的是sigmoid函数，所以预测数据的范围在0和1之间。

1.2 Head对象内部的计算流

上图对应的实现在ntm-lasagne/ntm/heads.py中的Head基类中的get_output_for函数

    def get_output_for(self, h_t, w_tm1, M_t, **kwargs):
        if self.sign is not None:
            sign_t = self.sign.get_output_for(h_t, **kwargs)
        else:
            sign_t = 1.
        k_t = self.key.get_output_for(h_t, **kwargs)
        beta_t = self.beta.get_output_for(h_t, **kwargs)
        g_t = self.gate.get_output_for(h_t, **kwargs)
        s_t = self.shift.get_output_for(h_t, **kwargs)
        gamma_t = self.gamma.get_output_for(h_t, **kwargs)

        # Content Adressing (3.3.1)
        beta_t = T.addbroadcast(beta_t, 1)
        betaK = beta_t * similarities.cosine_similarity(sign_t * k_t, M_t)
        w_c = lasagne.nonlinearities.softmax(betaK)

        # Interpolation (3.3.2)
        g_t = T.addbroadcast(g_t, 1)
        w_g = g_t * w_c + (1. - g_t) * w_tm1

        # Convolutional Shift (3.3.2)
        w_g_padded = w_g.dimshuffle(0, 'x', 'x', 1)
        conv_filter = s_t.dimshuffle(0, 'x', 'x', 1)
        pad = (self.num_shifts // 2, (self.num_shifts - 1) // 2)
        w_g_padded = padding.pad(w_g_padded, [pad], batch_ndim=3)
        convolution = T.nnet.conv2d(w_g_padded, conv_filter,
            input_shape=(self.input_shape[0], 1, 1, self.memory_shape[0] + pad[0] + pad[1]),
            filter_shape=(self.input_shape[0], 1, 1, self.num_shifts),
            subsample=(1, 1),
            border_mode='valid')
        w_tilde = convolution[:, 0, 0, :]

        # Sharpening (3.3.2)
        gamma_t = T.addbroadcast(gamma_t, 1)
        w = T.pow(w_tilde + 1e-6, gamma_t)
        w /= T.sum(w)

        return w

其中的传入参数解释如下：
h_t：controller的隐层输出；
w_tm1：前一时刻的输出值，即 wt−1 ;
M_t:Memory矩阵

1.3 NTMLayer结构图

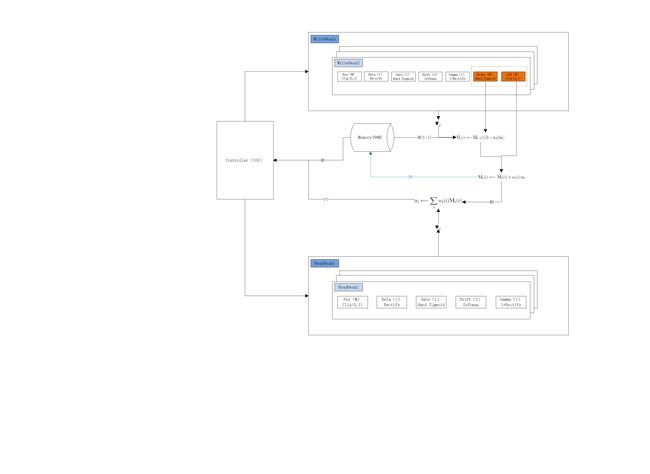
NTM层的数据处理实现在ntm-lasagne/ntm/layers.py中的NTMLayer.get_output_for函数中：

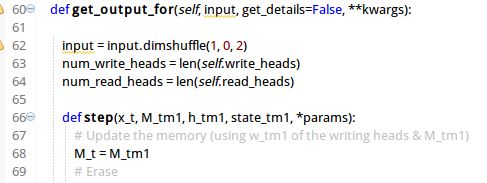
注意到其中还有一个内部函数step，这个函数中实现了每一次数据输入后NTM网络要进行的操作逻辑。
其中的参数解释如下：
x_t:当前的网络输入，即1.1中输入矩阵中的一行；
M_tm1：前一时刻的Memory矩阵，即 Mt−1
h_tm1:前一时刻的controller隐层输出
state_tm1:前一时刻的controller隐层状态，当controller为前馈网络时，等于前一时刻的输出
params：存放write heads和read heads上一时刻的输出即 wt−1 ,顺序如下:
[write_head1_w,write_head2_w,…,write_headn1_w,read_head1_w,read_head2_w,…,read_headn2_w]
1.每次网络接收到输入后，会进入step迭代函数，先走write(erase+add)流程，更新Memory，然后再执行read操作，生成 rt 向量。这部分代码如下：

最后的r_t就是读取出来的 rt 向量,注意这里有个比较特殊的参数W_hid_to_sign_add，这是一个开关参数，类似于LSTM中的“门”。这个参数默认为None。
2.read vector生成后，将作为输入参数被传入Controller：

3.step函数结束，返回值为一list，代码如下：

list中的元素依次为：[M_t, h_t, state_t + write_weights_t + read_weights_t]
step函数通过 theano.scan来进行迭代调用，每次的输入即为当前的input及上一时刻的list值
4.最后NTMLayer.get_out_for函数的返回值为：
hid_out = hids[1]，正好对应了Controller隐层最近一次的输出值。

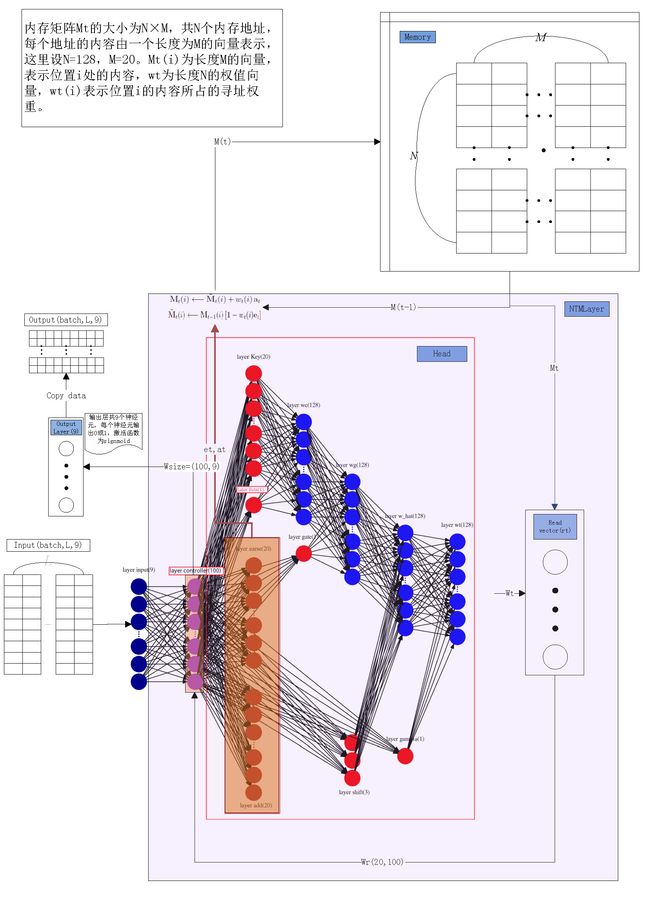
1.4 NTM网络结构图

2.公式及主要Class说明

αt=σalpha(htWalpha+balpha)
kt=σkey(htWkey+bkey)
βt=σbeta(htWbeta+bbeta)
gt=σgate(htWgate+bgate)
st=σshift(htWshift+bshift)
γt=σgamma(htWgamma+bgamma)

wct=softmax(βt∗K(αt∗kt,Mt))
wgt=gt∗wct+(1−gt)∗wt−1
w̃ t=st∗wgt
wt∝w̃ γtt

NTMLayer：父类为 lasagne.layers.Layer
功能：Neural Turing Machine的框架层
字段：memory：即Memory
controller：控制器，父类为Layer，默认100个节点
controller.hid_init：隐层的状态集合，大小为：（1,100）
heads：读写取Head集合
write_heads：写入Head集合
read_heads：读取Head集合
函数：get_output_for：在给定的输入input下，返回对应的输出值

Head:父类为lasagne.layers.Layer
功能：读写头的基类
字段：sign：DenseLayer（全连接网络），输出为 αt ，激活函数为ClippedLinear(-1,1),节点数：20；
key：DenseLayer,输出为 kt ，激活函数为ClippedLinear(0，1),节点数：20，输入层为controller；
beta：DenseLayer,输出为 βt ,激活函数为rectify，节点数：1，输入层为controller；
gate：DenseLayer,输出为 gt ,激活函数为hard_sigmoid，节点数：1，输入层为controller；
shift：DenseLayer,输出为 st ,激活函数为softmax，节点数：3（等于num_shifts，默认为3），输入层为controller，最终将输出3个概率值，分别对应 st(−1),st(0),st(1) ,s_{t}长度为N，除softmax输出的3个位置非0之外，其余位置为0；
gamma：DenseLayer,输出为 γt ,激活函数为1+rectify，节点数：1，输入层为controller；
num_shifts：卷积shifts的操作宽度(奇数)，当宽度为n时，移位向量为：[-n/2,…,-1,0,1,…,n/2]，比如，当n=3时，为：[-1,0,1]
weights_init：输出为OneHot 1×128 的权值向量，其初始值为除第一个元素为1之外，其余元素为0.
gate：DenseLayer,输出为 eraset ,激活函数为hard_sigmoid，节点数：20，输入层为controller；
add：DenseLayer,输出为 addt ，激活函数为ClippedLinear(0，1),节点数：20，输入层为controller；
rectify: f(x)=max(0,x)
sign_add：DenseLayer,输出为 signAddt ，激活函数为ClippedLinear(-1，1),节点数：20，输入层为controller；
rectify: f(x)=max(0,x)
softmax: f(x)=exj∑Kk=1exk

hard_sigmoid:

f(x)=⎧⎩⎨⎪⎪x=0,x<0x=0.2x+0.5,x∈[0,1]x=1,x>1

ClippedLinear(a,b):

f(x)={x=a,x<ax=b,x>b

3.copy-task实验

（待续）
参考文章：
http://blog.csdn.net/niuwei22007/article/details/49208643
https://medium.com/snips-ai/ntm-lasagne-a-library-for-neural-turing-machines-in-lasagne-2cdce6837315
http://lasagne.readthedocs.org/en/latest/user/tutorial.html
http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.imshow