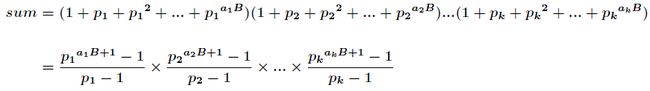POJ_1845_Sumdiv

题目：http://poj.org/problem?id=1845

 

题意：给定两个正整数和，求的所有因子和对9901取余后的值。

 

分析：很容易知道，先把分解得到，那么得到，那么

     的所有因子和的表达式如下

但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的，它们都会要求与互素。实际上我们还有一

种通用的求逆元方法，适合所有情况。公式如下

 

          

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#define LL long long
using namespace std;
const int MOD=9901;
LL multi(LL x,LL y,LL M)
{
    LL ans=0;
    while(y)
    {
        if(y&1)
        {
            (ans+=x)%=M;
        }
        (x+=x)%=M;
        y>>=1;
    }
    return ans;
}
LL power(LL x,LL n,LL M)
{
    x=x%M;
    LL ans=1;
    while(n)
    {
        if(n&1)
        {
            (ans=multi(ans,x,M))%=M;
        }
        (x=multi(x,x,M))%=M;
        n>>=1;
    }
    return ans;
}
int main()
{
   LL A,B;
   LL ans;
   LL cnt;
   LL M;
   while(cin>>A>>B)
   {
       ans=1;
       LL m=(LL)(sqrt(A+0.5));
       for(LL i=2;i<=m;i++)
       {
           if(A%i==0)
           {
               cnt=0;
               while(A%i==0)
               {
                   cnt++;
                   A/=i;
               }
               M=(i-1)*MOD;
                (ans*=(power(i,cnt*B+1,M)+M-1)/(i-1))%=MOD;
           }
       }
       M=(A-1)*MOD;
       if(A>1)
       {
           (ans*=(power(A,B+1,M)+M-1)/(A-1))%=MOD;
       }
       printf("%lld\n",ans);
   }
    return 0;
}