主成分分析法以及python实现

本文主要介绍一种降维算法，主成分分析法，Principal Components Analysis,简称PCA,这种方法的目标是找到一个数据近似集中的子空间，至于如何找到这个子空间，下文会给出详细的介绍，PCA比其他降维算法更加直接，只需要进行一次特征向量的计算即可。（在Matlab,python,R中这个可以轻易的用eig()函数来实现）。
假设我们给出这样一个数据集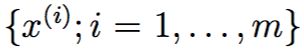代表m辆不同种类的汽车，每个数据点各个属性代表该类汽车的最大速度，转弯半径等等，假设对每个i都有(n << m)但是有一点我们不知道，对于某些Xi和Xj来说，最大时速是用不同的单位给出的，一个是用mile/hour,一个是用kilometers/hour,这两个属性显然是线性相关的，至于有一些不同是因为在mph和kph之间的转换造成的，因此，数据其实是近似集中在一个n-1维的子空间里的，我们如何自动侦测并且移除这些冗余呢？

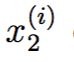再举一个更加具体的例子，我们现在拥有一个由对遥控直升机飞行员的问卷调查得出的数据集，第i个数据点的第一个分量代表该飞行员的飞行技巧，第二个分量表示TA对飞行过程的享受程度，因为遥控直升机非常难以操控，所以只有那些真正享受这个过程的人才能成为一个好的飞行员，所以,这两个属性具有很强的关联性，，实际上，我们可以假设数据实际集中在看起来像是一个斜的坐标轴附近，我们可以把这个坐标轴直观理解为一个人与飞行的”缘分”，（这样的直观理解可以帮助理解PCA）,如下图所示，我们如何自动计算出u1这个方向呢？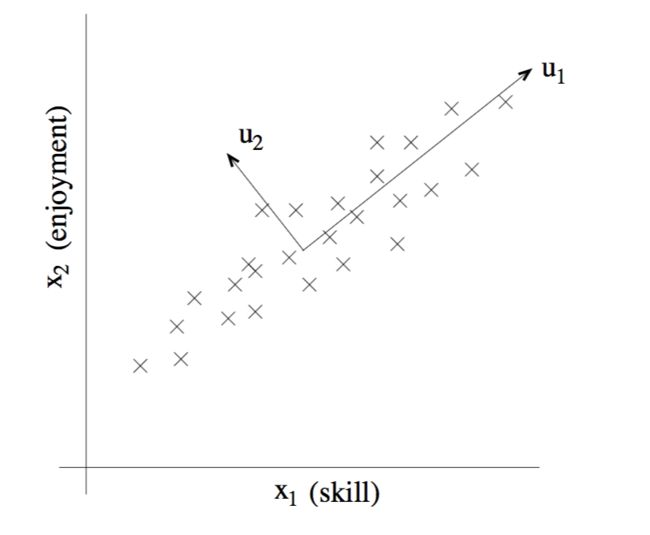

没错，计算u1这个方向的方法就是PCA算法，但是在数据集上运行PCA算法之前，通常我们要首先对数据进行预处理来标准化数据的均值和方差。下面是预处理过程：

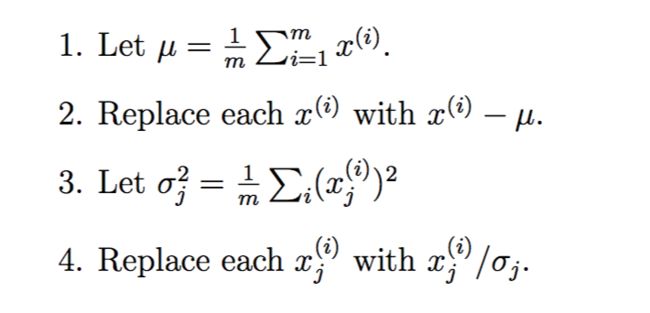
步骤1-2是为了让整个数据集的均值为0，如果这个数据集的均值已经是0，则这两步可以忽略，步骤3-4更新了每个属性的数据使得在同一个属性上的数据具有单位方差（归一化），从而保证不同的属性都有相同的数据范围而受到“平等对待”，打个比方，如果属性x1表示汽车的最快时速，用mph来表示，数据范围通常在大几十到一百多，x2表示汽车的座位数，数据范围通常在2-4，此时就需要重新标准化这两个不同的属性使他们更有可比性，当然，如果我们已经得知不同的属性具有相同的数据规模时，步骤3-4就可以忽略不做，例如当每个数据点代表一个灰度图像时,此时每个都是从{0,1……,255}中取值的。

现在，我们已经执行了数据的标准化，接下来该计算“数据差异主要所在”的轴u,即数据主要集中的方向，解决这个问题的方法是找到一个单位向量u使得当数据投影到这个方向时，投影数据的方差最大化,直观上理解，数据集中包含了数据的方差和数据信息，我们应该选择一个方向u使得我们能近似的让这些数据集中在u代表的方向或者子空间上，并且尽可能的保留这些数据的方差。

考虑下面的数据集合，对于这个数据集合我们已经执行了标准化步骤：

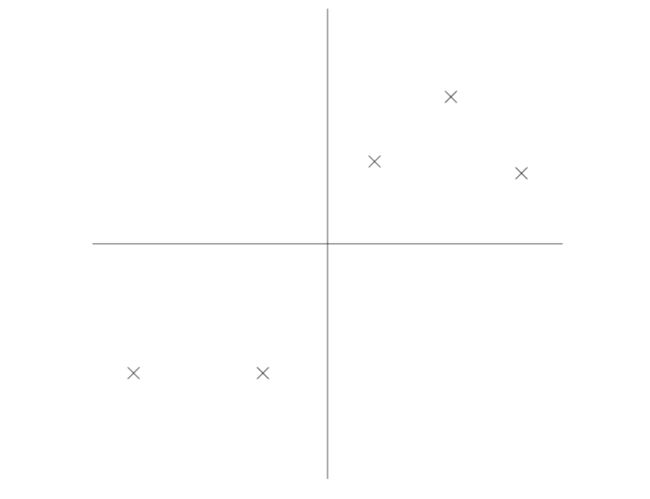
现在，假设我们选出了一个u代表下图中的方向，黑点代表了原始数据在这条线上的投影，

在上图中，我们看到投影数据仍然具有相当大的方差，并且这些点都远离原点，我们来看看另外一种情况，假设选出的u是下图这种方向的：

在这张图中，可以明显的观察到投影的方差明显比上图小很多，并且投影数据更加接近原点。
所以，我们想要通过某种算法来挑选出方向u对应于上面两张图中的前者的方向，为了用标准数学语言描述，假设有一个单位向量u和一个点x，则x投影在u上的长度为等价的说法就是，如果xi是现有数据集中的一个点（用图中的一个叉来表示），则它在u上的投影（图上的黑点）到原点的距离为，因此，为了使投影的方差最大化，我们需要挑选出一个单位向量使得下面的式子取得最大值：

我们可以比较容易的通过拉格朗日乘数法发现当上面的式子取最大值时u取这个矩阵的主特征向量即可，通过观察，我们发现这个矩阵恰好是原始数据集的协方差矩阵。
总结一下，我们发现如果我们希望找到一个一维子空间来近似简化数据集，我们只需要计算出的主特征向量u即可，推广到高维空间来说，如果我们把我们的数据集投影到k-维子空间(k< n),我们就应该用矩阵前k大的特征向量来作为u1,u2,…..uk，也就是说ui现在组成了数据集上一组新的基。之后，为了表示xi在这组新的基下的坐标，我们只需要计算对应的数据向量即可这样，原始数据向量yi现在位于一个比n维更低的，k-dim的子空间，用来近似代替或者完全代替xi,因此PCA也被称之为一种降维算法，向量u1,u2,…..uk被称作数据集的前k个主成分。
PCA有很多的应用场景，首先，压缩是一个明显的用途—用yi来代替xi,如果我们用高维数据集缩减为k=2或者3维，我们就可以画出yi从而使数据可视化，打个比方，如果我们将数据集缩减到二维，然后我们就可以把数据画到坐标平面里(图中一个点代表一类车型),然后观察哪些车型是类似的，哪一类车型可以被聚类。

其他的标准用途包括在运行监督学习算法之前对数据集进行预处理使维度减少，除了可以减少计算开销之外，减少数据的维度同样可以减少考虑假设分类的复杂程度同时避免过度拟合。

下面提供一个python的pca实现，为了直观的描述pca算法，使用一个1000*2的矩阵作为测试数据集，降到1维，并画出图像来进行观察，首先查看一下我们的测试数据文件前十个数据点，（如果你需要这个测试数据集，可以发送给你。）

之后我们运行利用python实现的pca算法并且画图，代码如下：

from numpy import * def loadDataSet(fileName,delim=‘\t‘): fr=open(fileName) stringArr=[line.strip().split(delim) for line in fr.readlines()] datArr=[map(float,line) for line in stringArr] return mat(datArr) def pca(dataMat,topNfeat=9999999): meanVals=mean(dataMat,axis=0) meanRemoved=dataMat-meanVals covMat=cov(meanRemoved,rowvar=0) eigVals,eigVets=linalg.eig(mat(covMat)) eigValInd=argsort(eigVals) eigValInd=eigValInd[:-(topNfeat+1):-1] redEigVects=eigVets[:,eigValInd] print meanRemoved print redEigVects lowDDatMat=meanRemoved*redEigVects reconMat=(lowDDatMat*redEigVects.T)+meanVals return lowDDatMat,reconMat dataMat=loadDataSet(‘testSet.txt‘) lowDMat,reconMat=pca(dataMat,1) def plotPCA(dataMat,reconMat): import matplotlib import matplotlib.pyplot as plt datArr=array(dataMat) reconArr=array(reconMat) n1=shape(datArr)[0] n2=shape(reconArr)[0] xcord1=[];ycord1=[] xcord2=[];ycord2=[] for i in range(n1): xcord1.append(datArr[i,0]);ycord1.append(datArr[i,1]) for i in range(n2): xcord2.append(reconArr[i,0]);ycord2.append(reconArr[i,1]) fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(xcord1,ycord1,s=90,c=‘red‘,marker=‘^‘) ax.scatter(xcord2,ycord2,s=50,c=‘yellow‘,marker=‘o‘) plt.title(‘PCA‘) plt.show() plotPCA(dataMat,reconMat) 

最后的降维结果如图所示

主成分分析法原理及其python实现