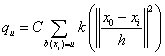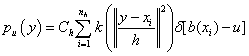MeanShift算法(二)之运动目标跟踪
根据上篇文章,MeanShift算法(一),了解了MeanShift算法的最基本理论。推导了如何利用核密度估计函数和密度梯度估计以及轮廓函数得到mean shift向量。可是有了这么一个理论总需要把它应用在某个领域里吧。那么现在就开始进入MeanShift运动目标跟踪的世界。以前在别人的博客里看见有人说MeanShift算法现在已经不常用了,貌似被淘汰了,真假难辨?就算是真的,学习这一种算法那也能为以后理解其它算法打下一定基础。在运动目标跟踪领域,Kalman Filter, Particle Filter 和 MeanShift是我目前唯一知道的几种方法了,如果有牛人知道其它更有效的方法,还望不吝赐教!!我想这个也因应用场景不同跟踪效率和精确度等也不一样吧。本文大多部分来自其他文章,起到一个总结作用。。。
再谈MeanShift的应用:
MeanShift可以应用在很多领域,比如聚类,图像平滑,图像分割。尤其是应用在目标跟踪领域,其跟踪算法是通过计算候选目标与目标模板之间相似度的概率密度分布,然后利用概率密度梯度下降的方向来获取匹配搜索的最佳路径,加速运动目标的定位和降低搜索的时间,因此在目标实时跟踪领域有着很高的应用价值。该算法由于采用了统计特征,因此对噪声有很强的鲁棒性;由于是一个单参数算法,容易作为一个模块和别的算法集成;采用核函数直方图建模,对边缘阻挡、目标的旋转、变形以及背景运动都不敏感;同时该算法构造了一个可以用MeanShift算法进行寻优的相似度函数。由于MeanShift本质上是最陡下降法,因此其寻优过程收敛速度快,使得该算法具有很好的实时性。
均值漂移在目标跟踪中的应用:
一:目标模型的描述
1)在起始帧,通过鼠标确定一个包含所有目标特征的椭圆,称为被跟踪目标的目标区域,这个区域也是核函数作用的区域,区域大小等于核函数的带宽;
2)对目标区域进行描述,常用的方法是按照直方图的方式将像素的值域分成k个区间。每个区间按照值域的大小对应一个特征值。然后求出图像的像素值取每个特征值的概率;
3)对在初始帧图像中目标区域内所有的像素点,计算每个特征值的概率,可称为目标模型的描述。
目标区域的中心为x0,假设其中有n个像素用{xi}i=1…n表示。特征值得的个数为m个,则目标模型特征值为u=1...m,其概率密度估计为:
加入高斯核函数后为:
在有些文献文献中,上式被写为如下形式:
几点说明:
1)特征值概率密度估计函数两种写法中本质都一样,个人认为第二种写法更好理解。因为b(xi)是颜色灰度级的索引函数,与特征值u作比较,和u相等为1,否则为0;
2)k(x)为函数的轮廓函数。由于遮挡或者背景的影响,目标模型中心附近的像素比外物像素更可靠。k(x)给中心像素一个大的权值,而远离中心的像素给一个小的权值;
4)由此可以得到基于图像灰度特征的颜色直方图。
二:候选模型的描述(candidate model)
运动目标在第二帧及以后的每帧中可能包含目标的区域称为候选区域,其中心坐标为y,也是核函数的中心坐标。该区域中的象素用{xi}i=1…nh(h为下标)表示。对目标候选模型的特征u=1...m的概率密度表示为:
其中为标准化常量。
三:相似性函数(similarity function)
模板区域:
候选区域:
相似性函数的定义:
![]()
根据Bhattacharyya系数:
![]()
相似性函数描述目标模型和候选模型之间的相似程度,在理想情况下两个模型的概率分布是完全一样的。其值在0到1之间,若值越大则两个模型越相似。
四:目标定位
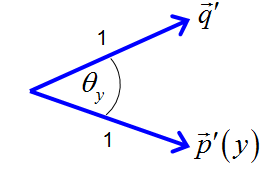
为使f(x)最大,将当前帧的目标中心先定位为前一帧中目标中的位置y0;从这一点开始寻找最优匹配的目标,其中心为y。可将f(x)展开为:
由于第一项独立于y之外且数值小于1,因此这里忽略不计。根据
第二项可以表示为:
,由此化为关于y的密度估计函数。
其中:。
类似于核函数密度估计,只是多了一个权值w,使得相关性函数的取值最大。令:
计算fn,K的mean shift向量,这样就可以得到候选区域中y0移向真实区域y的向量:
其中![]() 。值得注意的是,一般在一帧中找到目标的位置,需要MeanShift算法从开始若干次迭代才能得到。
。值得注意的是,一般在一帧中找到目标的位置,需要MeanShift算法从开始若干次迭代才能得到。
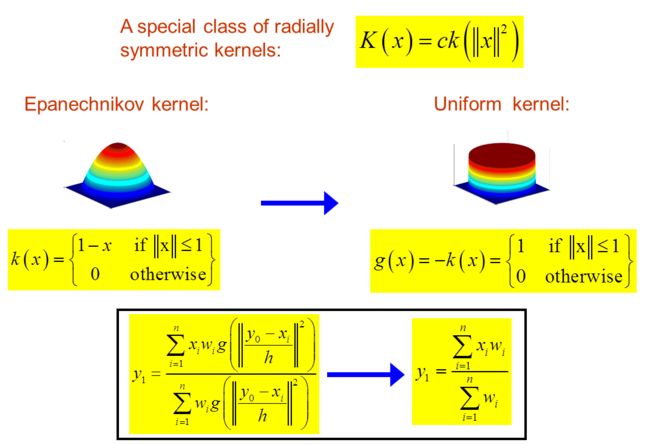
化简:截个图,下图的意思是因为核函数都是径向对称函数,由于Epanechnikov核和高斯核的轮廓函数都是各向同性,所以可将y1化为:
对上图理解水平有限,还需思考。。。
五:整个算法流程
1)在当前帧以y0为起点,计算候选目标的特征{pu(y0)}u=1,2…..m;
2)计算候选目标与目标的相似度;
3)计算权值{wi}i=1,2…..m;
4)利用MeanShift算法,计算目标新位置
;
5)若,则停止;否则y0←y1转步骤2)。
限制条件:新目标中心需位于原目标中心附近。
六:MeanShift算法的优缺点
优点:
1) 算法复杂度小;
2) 是无参数算法,易于与其它算法集成;
3) 采用加权直方图建模,对目标小角度旋转、轻微变形和部分遮挡不敏感等。
缺点:
1) 搜索窗的核函数带宽保持不变;
2) 缺乏必要的模板更新算法;
3) 目标的运动不能过快;
4) 当颜色区域为均匀的时候,对h来说相似性是不变的;