百钱买百鸡之数学优化

文言文：

今有鸡翁一，值钱伍；鸡母一，值钱三；鸡鶵三，值钱一。凡百钱买鸡百只，问鸡翁、母、鶵各几何？答曰：鸡翁四，值钱二十；鸡母十八，值钱五十四；鸡鶵七十八，值钱二十六。又答：鸡翁八，值钱四十；鸡 母十一，值钱三十三，鸡鶵八十一，值钱二十七。又答：鸡翁十二，值钱六十；鸡母四、值钱十二；鸡鶵八十 四，值钱二十八。”-------《张邱建算经》

链接：http://baike.baidu.com/view/367996.htm

现代文：公鸡每只值5 文钱，母鸡每只值3 文钱，而3 只小鸡值1 文钱。现在用100 文钱买100 只鸡，问：这100 只鸡中，公鸡、母鸡和小鸡各有多少只？

设公鸡个数为X，母鸡个数为Y，鸡仔个数为Z。

则有约束条件：0<=X,Y,Z>=100；X+Y+Z = 100；5X + 3Y + Z/3 = 100

隐含约束条件：Z%3 = 0，因为鸡肯定是整只的（肯德鸡除外）。所以鸡仔的个数是3的倍数。

根据约束条件有如下解法：

1）

直接法（蛮力法，穷举法）：

#include <iostream>
int main()
{
    int x,y,z;
    int count = 0;
    for(x=0;x<=100;x++){
        for(y=0;y<=100;y++){
            for(z=0;z<=100;z++){	
            count++;//计算穷举次数 
            if (z%3==0 &&x*5+y*3+z/3==100&&x+y+z == 100)
                std::cout<<"公鸡: "<<x<<" 母鸡: "<< y << " 小鸡: "<<z<<std::endl;
            }
        }
    }  
    std::cout << count;
    return 0;
}

这个方法三层for循环，的算法复杂度是0（n^3），穷举次数是100万级别，简直不能忍

2）数学初步优化

再考虑一下题设条件：

全部钱买公鸡可以买100/5 = 20；全部钱买母鸡可以买约33个，而鸡仔是100 -（X+Y）

则约束条件为：0<= X<=20；0<=y<=33；Z = 100 -（X+Y）；Z%3=0；

#include <iostream>
int main()
{
    int x,y,z;
    int count = 0;
    for(x=0;x<=20;x++){
        for(y=0;y<=33;y++){
            count++;
			z=100-x-y;
            if (z%3==0 &&x*5+y*3+z/3==100)
              std::cout<<"公鸡: "<<x<<" 母鸡: "<< y << " 小鸡: "<<z<<std::endl;

        }
    }  
    std::cout << count;
    return 0;
}

枚举714次。对比第一个简直快了99/100。两层for循环，算法复杂度是O(n^2)

3）数学进一步优化

在 2）中的约束条件：0<= X<=20；0<= Y<=33；Z = 100 -（X+Y）；Z%3=0;

由 X+Y+Z = 100和5X + 3Y + Z/3 = 100可得7X+4Y=100

则Y = 25  - （7/4）X

再令X = 4K，则有Y = 25 - 7K，继而Z = 75 + 3K

因为  0=<  Z <=100，所以K的可能取值是0，1，2，3

#include<iostream>
int main()
{
    int x,y,z;
    int count = 0;
	for (int k = 0; k <= 3; k++){
		count ++;
        x = 4 * k;
		y = 25 - 7 * k;
        z = 75 + 3 * k;
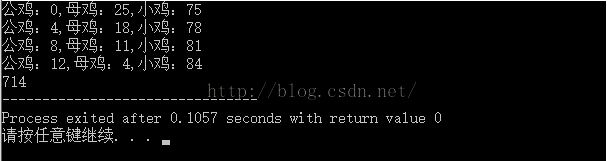
        std::cout<<"公鸡: "<<x<<" 母鸡: "<< y << " 小鸡: "<<z<<std::endl;
    } 
    std::cout << count;
    return 0;
}

一个for循环，可在常数时间内算出。