小波分析个例应用
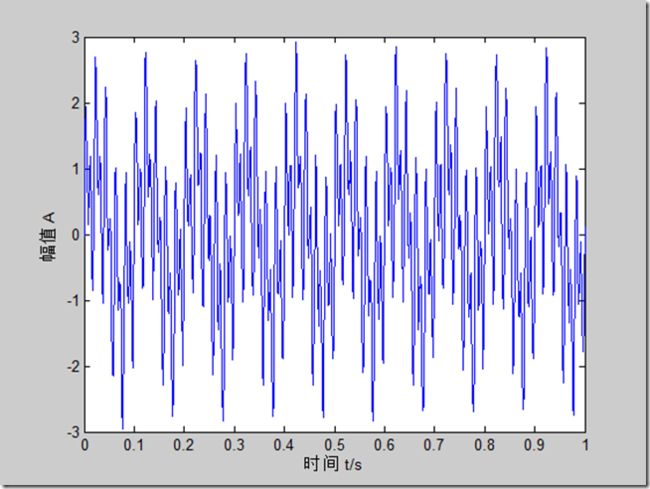
3个正弦波(10、50、100Hz)混合,再掺和上噪声,结果如下
小波分解,再重构各细节、近似信号如下
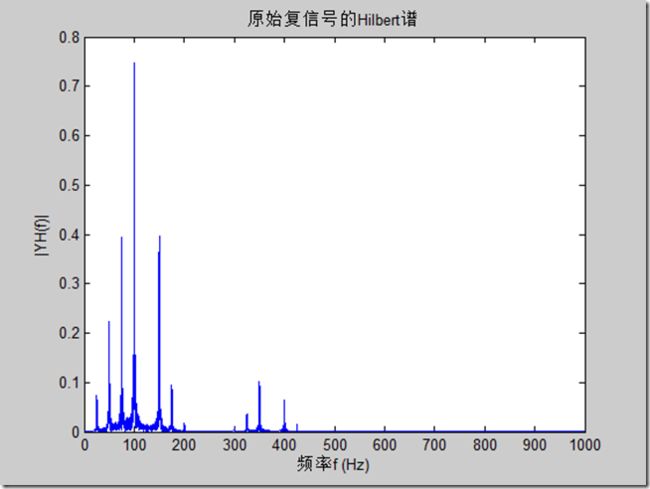
最后简单对一个细节信号d3做Hilbert谱分析
会发现,信号的倍频通过小波分析会很明显。
感觉小波的问题是,不知道选哪个细节或近似,貌似就是靠目测。好吧,以后多用用,积累经验吧!
代码如下
clc
clear all
close all
% 当前延拓模式是补零
oldmode = dwtmode('zpd');
ts = 0.001;
fs = 1/ts;
t=0:ts:1;
N = length(t);
x = sin(2*pi*10*t) + sin(2*pi*50*t) + sin(2*pi*100*t) + 0.1*randn(1, length(t));
figure
plot(t,x);
xlabel('时间 t/s');
ylabel('幅值 A');
% 一维小波分解
[c,l] = wavedec(x,5,'db3');
% 重构第1~5层逼近系数
a5 = wrcoef('a',c,l,'db3',5);
a4 = wrcoef('a',c,l,'db3',4);
a3 = wrcoef('a',c,l,'db3',3);
a2 = wrcoef('a',c,l,'db3',2);
a1 = wrcoef('a',c,l,'db3',1);
% 显示逼近系数
figure
subplot(5,1,1);plot(a5);ylabel('a5');
subplot(5,1,2);plot(a4);ylabel('a4');
subplot(5,1,3);plot(a3);ylabel('a3');
subplot(5,1,4);plot(a2);ylabel('a2');
subplot(5,1,5);plot(a1);ylabel('a1');
xlabel('时间 t/s');
% 重构第1~5层细节系数
d5 = wrcoef('d',c,l,'db3',5);
d4 = wrcoef('d',c,l,'db3',4);
d3 = wrcoef('d',c,l,'db3',3);
d2 = wrcoef('d',c,l,'db3',2);
d1 = wrcoef('d',c,l,'db3',1);
% 显示细节系数
figure
subplot(5,1,1);plot(d5);ylabel('d5');
subplot(5,1,2);plot(d4);ylabel('d4');
subplot(5,1,3);plot(d3);ylabel('d3');
subplot(5,1,4);plot(d2);ylabel('d2');
subplot(5,1,5);plot(d1);ylabel('d1');
xlabel('时间 t/s');
% 第1层细节信号的包络谱
yh = hilbert(d3);
aabs = abs(yh); % 包络的绝对值
aabs = aabs - mean(aabs);
aangle = unwrap(angle(yh)); % 包络的相位
af = diff(aangle)/2/pi; % 包络的瞬时频率,差分代替微分计算
% NFFT = 2^nextpow2(N);
NFFT = 2^nextpow2(1024*4); % 改善栅栏效应
f = fs*linspace(0,1,NFFT);
YH = fft(yh, NFFT)/N; % Hilbert变换复信号的频谱
A = fft(aabs, NFFT)/N; % 包络的频谱
figure
plot(f,abs(YH))
title('原始复信号的Hilbert谱')
xlabel('频率f (Hz)')
ylabel('|YH(f)|')
figure
subplot(221)
plot(t, aabs')
title('包络的绝对值')
legend('包络分析结果', '真实包络')
subplot(222)
plot(t, aangle)
title('调制信号的相位')
subplot(223)
plot(t(1:end-1), af*fs)
title('调制信号的瞬时频率')
subplot(224)
plot(f,abs(A))
title('包络的频谱')
xlabel('频率f (Hz)')
ylabel('|A(f)|')
% 恢复延拓模式
dwtmode(oldmode);