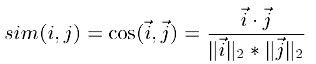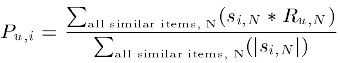[置顶] Pearson 相关系数--最佳理解及相关应用

一 Pearson 相关系数介绍

       pearson是一个介于-1和1之间的值，用来描述两组线性的数据一同变化移动的趋势。

    当两个变量的线性关系增强时，相关系数趋于1或-1；

     当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；

     如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；

     如果相关系数等于0，表明它们之间不存在线性相关关系。

用数学公式表示，皮尔森相关系数等于两个变量的协方差除于两个变量的标准差。（标准差 就是方差的开方）

   

协方差（Covariance）：在概率论和统计学中用于衡量两个变量的总体误差。如果两个变量的变化趋于一致，也就是说如果其中一个大于自身的期望值，另一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，则协方差为负值。

其中u表示X的期望E(X), v表示Y的期望E(Y)

由于pearson描述的是两组数据变化移动的趋势，所以在基于user-based的协同过滤系统中，经常使用。描述用户购买或评分变化的趋势，若趋势相近则pearson系数趋近于1，也就是我们认为相似的用户。

Pearson 相关系数的缺陷

直观的可以看出，pearson不适用于文本的相似性分析。

pearson存在以下3个问题： 以下图的数据作为测试用例

1. 未考虑重叠记录项的数量对相似度的影响

    上表中，行表示用户（1～5）对项目（101～103）的一些评分值。直观来看，User1和User5用3个共同的评分项，并且给出的评分趋势相
同，User1与User4只有2个相同评分项，虽然他们的趋势也相似，但是由于102的未知，可能是User2对102未发生行为，或者对102很讨厌，所以我们更希望User1和User5更相似，但结果是User1与User4有着更高的结果。
     可以看出pearson系数只会对重叠的记录进行计算。

     同样的场景在现实生活中也经常发生，比如两个用户共同观看了200部电影，虽然不一定给出相同或完全相近的评分，但只要他们之间的趋势相似也应该比另一位只观看了2部相同电影的相似度高！但事实并不如此，如果对这两部电影，两个用户给出的相似度相同或很相近，通过Pearson相关性计算出的相似度会明显大于观看了相同的200部电影的用户之间的相似度。

2.如果只有一个重叠项则无法计算相关性

    从数学上讲，若只有一个重叠的记录，那么至少有一组记录的标准差为0，导致分母为0
从这一点也可以看出，pearson系数不适用与小的或者非常稀疏的数据集。当然，这一特性也有它的好处，无法计算pearson系数可以认为这两组数据没有任何相关性。

3.如果一组记录的所有评分都一样则无法计算相关性

    理由同2.

4.Pearson系数对绝对数值不敏感

    考虑这三组数据，1:(1.0,2.0,3.0,4.0),2:(40.0,50.0,70.0,80.0),3:(50.0,60.0,70.0,80.0),我们可以直观的认为2和3更为相似，它们的重叠评分数目一致，趋势也相同，记录1虽然也满足上述的条件，但是它整体数值很低。在现实中，有人习惯于给出更高的评分，而有人则恰恰相反。
    利用pearson计算它们之间的相似度为：
     1&2: 0.9899494936611665

     2&3: 0.9899494936611665

     1&3: 0.9999999999999999

    可以看出pearson系数对绝对数值并不敏感，它确实只是描述了两组数据变化的趋势。

二 浅述协同过滤之基于用户的最近邻推荐【结合pearson系数】

         协同过滤的推荐方法有很多，其主要思想是利用已有的大量用user set的历史行为数据
来预测当前user的对哪些东西最感兴趣或是最喜欢哪些东西。 

    【 user对各Item的评分构成特征向量矩阵】

    纯粹的协同方法的输入数据只有给定的user-item的评分矩阵，输出数据通常有下列类型：

       1）标识当前user对于item喜欢或是不喜欢程度的预测数据

       2）n项推荐item的列表，这是topN的列表，当前user购买过的item不会在此列表内

下面说说user-based nearest neighbor recommendation.

基于user的最近邻推荐的基本思想是：

1）给定一个user-item构成的评分矩阵，找出与当前user在过去有相似偏好的其他用户，也就是找近邻的过程

2）对于当前user没有见过的item，利用user的近邻对item的历史评分来计算user对item的偏好程度的预测值

上述思想的隐含假设是：

1）假如user间过去有相似的偏好，那么这些user将来也会有相似的偏好

2）user对item的偏好不会随时间而变化

至于如何确定相似user set，推荐系统中常用的方法是Pearson相关系数。

        Pearson相关系数取值从强正相关（+1）到强负相关（-1）。 

       Pearson方法充分考虑到了user对item的评分标准并不相同，有些user喜欢只给item高分，而另一些user从不任何item满分。同时，Pearson相关系数在计算中未考虑user对item偏好评分的平均值的差异使得user可比，也就是说即使两个user对item偏好的绝对评分值完全不同，但仍然可以发现user对item的评分值之间相当明显的线性相关性，进而得出两个user相似的结论。【Pearson系数对绝对数值不敏感】

       在实际应用中，评分数据集通常非常大，而且包括了成千上万甚至百万级的user和item，这就要求必须考虑时间复杂度。此外，评分矩阵通常非常稀疏，每个user只对所有有效item的非常小的一个子集评分。还需要考虑给新的user推荐什么item，该如何处理没有评分的新item。

         除了Pearson相关系数衡量user间的相似度，改进的余弦相似度、Spearman秩相关系数、均方差等也能用于计算user间的相似度。

        但是实验分析显示，对于user-based推荐系统来说，Pearson相关系数比其它对比方法更胜一筹。但是Pearson方法发现近邻以及为这些近邻的评分赋权可能还不是最好的选择。

       比如，很多领域会有一些所有user都会喜欢的item，让两个user对有争议的item达成共识会比对广受欢迎的item达成共识更有价值，但Pearson这样的相似度方法无法将这种情况考虑在内。当然IUF和方差权重因子等可以解决这样的问题。

     另外，对于近邻评分的预测方法在遇到当前user只为非常少的共同item评分时会出错，导致不准确的预测。重要性赋权和样本扩展等方法都在探索此类问题的解决。

在user近邻选择时不用考虑use的所有近邻。为了减少计算与测试时的时间复杂度，只包括了那些与当前user有正向关联的user。降低近邻集合规模的通常方法是为user相似度定义一个具体的最小阈值，或者将规模大小限制为一个固定值，而且只考虑k近邻。当然相似度阈值过高，近邻规模就会很少，也就降低了覆盖率。如果太低，近邻规模就不会显著降低。对于k近邻，k太高，太多只有有限相似度的近邻会给预测带来额外的“噪声”；k太小，预测质量会受到负面影响。对MovieLens数据集的分析发现：在大多数情况下，20-50个近邻比较合理。

三  浅述协同过滤之基于物品的最近邻推荐

         在很多领域都使用了user-based CF的方法。但是user-based CF的方法也存在问题。

首先，基于user的最近邻算法的计算量会随着item和user的数量的增加而增加，在数据量非常大的时候，要求实时地计算预测          值难以做到。

另外，在一些大型的电商网站上，都拥有数以百万计的用户和物品，由于用户实际购买的物品非常少，且不同用户之间购买的物品的重叠性非常低，就是导致算法找不到有相似偏好的用户。在计算用户的最近邻时，难以实时地计算预测值。

       然而，基于item-based CF却非常适合在线下进行处理。而且，在评分矩阵非常大的情况下也能做到实时推荐。

       item-based CF的主要思想是基于用户的历史数据来计算物品的相似度，利用物品间的相似度取代用户间的相似度进行推荐，然后把和用户偏好的物品非常相似的物品推荐给用户。

       首先需要制定相似度度量标准，用以计算物品间的相似度。 在信息检索和文本挖掘中广泛使用的余弦相似度，在基于物品的推荐方法中，效果也非常好，已经被当作标准的度量体系。一般的计算方法有：

       1）基于余弦的相似度计算，通过计算两个向量之间的夹角余弦值来计算物品之间的相似度，计算公式如下： 

                                                   

其中，分子为两个向量的内积，即两个向量相同位置的数字相乘。分母是两个向量的欧式长度的乘积，即向量自身点积的平方根的乘积。计算得到的相似度取值介于0和1之间，越接近于1表示两个物品越相似。这种基本的余弦相似度的计算方法并没有考虑用户评分平均值的差异，用户打分起点有差异。

2）基于关联的相似度计算，计算两个向量之间的Pearson-r关联度，计算公式如下：

                                           

其中表示用户u对物品i的打分，表示第i个物品打分的平均值。。

3）调整的余弦相似度计算，以为基于余弦的相似度计算方法未考虑用户的差异性打分情况，有些用户偏倾向于打高分，而有些用户倾向于打低分，在计算相似度时通过减去用户各种打分的均值以消除不同用户打分起点的影响，公式如下：

                                                

               其中 表示用户u打分的均值。相应地，改进的余弦方法的取值在-1和+1之间，就像pearson方法一样。

       其次，确定了物品和其它物品的相似度之后，基于这个数据就可以预测用户对物品的评分。 在计算时，对近邻集合的规模会进行限制。一般地对用户未打分的物品进行预测的方法有：

       1）加权求和。该方法的过程是：对用户u打分过的物品的分数进行加权求和，权值为用户u打分过的物品与物品i的相似度，然后对所有物品相似度的和求平均，计算得到用户u对物品i打分，公式如下：

                                                       

        其中 为物品i与物品N的相似度， 为用户u对物品N的打分。这种方法会有一个问题：不同用户的打分习惯会有差异，有的倾向于打高分，有的倾向于打低分，这就导致不同用户对喜欢的相同物品给分不会相同。使用余弦相似度计算时，欧式距离就会很大，但事实是相似度本应很高。在这种情况下使用用户原始的相似物品打分值进行计算会严重影响实际的预测结果。

       2）回归。 为了解决加权求和中提到的问题，回归的方法不直接使用相似物品N的打分值 ，而是通过线性回归的方式重新估算新的 值，然后依然使用上面的方法进行预测。重新计算 的方法如下：                                                                      

                                                             

        其中物品N是物品i的相似物品， 和 通过对物品N和i的打分向量进行线性回归计算得到， 为回归模型的误差。

传统基于用户协同过滤的问题是，算法不能很好的适应大规模用户和物品的数据。给定M个用户和N个物品，在最坏的情况下，必须评估最多包含这N个物品的所有M个用户的记录。在实际情况下，由于大多数用户只评分或购买了非常少量的物品，实际复杂度非常低。尽管如此，当用户的数据M打到几百万是，线上环境要求必须在极端事件内返回结果时，实时计算预测值仍不可行。

        为了在不牺牲推荐精度的情况下，在大规模的电子商务网站上应用基于物品的推荐算法，通过离线计算预测数据。其想法是事先构建一个物品相似度矩阵，描述所有物品两两之间的相似度。在运行时，通过确定与p最相似的物品并计算u对这些近邻物品评分的加权总和来得到用户u对物品p的预测评分。近邻数量受限于用户当前评过分的物品数。由于这样的物品数量一般都比较少，一次计算预测值可以在线上交互应用允许的时间内完成。

       考虑到内存要求，N个物品的相似度矩阵理论上有N2项，但时间项数会极低，而且还可以采取进一步的方法降低复杂度。可选的方案是，仅仅考虑哪些月其它物品同事评分数最小的物品，或者对每个物品只记录有限的近邻。然而这种方法会增加无法预测某个特定物品的风险。

原则上，这种离线预计算近邻的方法对基于用户的方法也适用。但在实际情况下，两个用户评分重叠的情况非常少见，这就意味着一些其他的评分值可能影响到用户间的相似度。相对用户相似度而言，物品相似度更稳定，这种预处理计算不会过于影响预测准确度。

        除了这些所谓基于模型的方法中采用的不同预处理计算之外，还可以仅仅利用评分矩阵中的某一部分以降低计算复杂度。一种基本技术是二次采样，这种技术可以随机选取数据的子集，或者忽略哪些仅有非常少量评分活仅包含非常热门物品的用户记录。Yu et al.(2003)也提出过一种更加高级且基于信息论的技术过滤最“相关”的用户。一般来说，可以用这些技术加速计算，但由于推荐用到的信息少了，系统做出精确预测的能力肯能会下降。

       对于上述问题的解决方案，有兴趣的可以进一步研究研究。

参考：

      http://www.xiutx.cn/