HihoCoder Trie树 java实现
太晚知道知道这个平台了,还是接到MS的笔试通知后才得知,平台真不错。
言归正传,问题描述:
1014 : Trie树
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho是一对好朋友,出生在信息化社会的他们对编程产生了莫大的兴趣,他们约定好互相帮助,在编程的学习道路上一同前进。
这一天,他们遇到了一本词典,于是小Hi就向小Ho提出了那个经典的问题:“小Ho,你能不能对于每一个我给出的字符串,都在这个词典里面找到以这个字符串开头的所有单词呢?”
身经百战的小Ho答道:“怎么会不能呢!你每给我一个字符串,我就依次遍历词典里的所有单词,检查你给我的字符串是不是这个单词的前缀不就是了?”
小Hi笑道:“你啊,还是太年轻了!~假设这本词典里有10万个单词,我询问你一万次,你得要算到哪年哪月去?”
小Ho低头算了一算,看着那一堆堆的0,顿时感觉自己这辈子都要花在上面了…
小Hi看着小Ho的囧样,也是继续笑道:“让我来提高一下你的知识水平吧~你知道树这样一种数据结构么?”
小Ho想了想,说道:“知道~它是一种基础的数据结构,就像这里说的一样!”
小Hi满意的点了点头,说道:“那你知道我怎么样用一棵树来表示整个词典么?”
小Hi于是在纸上画了一会,递给小Ho,道:“你看这棵树和这个词典有什么关系?”
小Ho盯着手里的纸想了一会道:“我知道了!对于从树的根节点走到每一个黑色节点所经过的路径,如果将路径上的字母都连起来的话,就都对应着词典中的一个单词呢!”
小Hi说道:“那你知道如何根据一个词典构建这样一棵树么?”
“不造!”
“想你也不知道,我来告诉你吧~”小Hi摆出一副老师的样子,说道:“你先这么想,如果我已经有了这样的一个词典和对应的一棵树,我要添加一个新的单词apart,我应该怎么做?”
“让我想想……”小Ho又开始苦思冥想:“首先我要先看看已经能走到哪一步了对吧?比如我从1号节点走”a”这一条边就可以走到2号节点,然后从2号节点走”p”这一条边可以走到3号节点,然后……就没路可走了!这时候我就需要添加一条从3号节点出发且标记为”p”的边才可以接着往下走……最后就是这样了!然后我把最后到达的这个结点标记为黑色就可以了。”
小Hi说道:“真聪明~那你不妨再算算如果是一个有10W个单词的词典,每个单词的长度不超过10的话,这棵树会有多大?”
小Ho于是掏出笔来,一边画一遍念叨:“假设我已经将前三个单词构成了这样一棵树,那么我要添加一个新的单词的时候,最坏情况是这个单词和之前的三个单词都没有公共前缀,那么这个新的单词的长度如果是5的话,我就至少要添加5个结点到树中才能够继续表示这个词典!”
“而如果每次都是最坏情况的话,这棵树最多也就100W个结点这么大!更何况最坏情况是不可能次次都发生的!毕竟字母表也才26个字母呢!”小Ho继续说道。
“嗯~这样我们是不是就可以用(单词个数*单词长度)个结点来表示一个词典了呢?小Hi问道。
“是的呢!”小Ho道:“但是这样一棵树又有什么用呢?”
“可别小看了它,它就是传说中的Trie树哦~至于他有什么用,一会你就知道了!”小Hi笑嘻嘻的回答道。
“你看,我们现在得到了这样一棵树,那么你看,如果我给你一个字符串ap,你要怎么找到所有以ap开头的单词呢?”小Hi又开始考校小Ho。
“唔…一个个遍历所有的单词?”小Ho还是不忘自己最开始提出来的算法。
“笨!这棵树难道就白构建了!”小Hi教训完小Ho,继续道:“看好了!”
小Hi在树上用绿色标出了一个节点,递给小Ho。
“这个结点……是从根节点先走”a”然后走”p”到达的结点呢!哦~~我知道了,以这个结点为根的子树里所有标记结点都是以”ap”为前缀的单词呢!而且所有以”ap”为前缀的单词都在以这个节点为根的子树里~”小Ho惊喜道。
“是的呢~那你对怎么解决我的问题有想法了么?”小Hi追问道。
“唔…那就是每次拿到你的字符串之后,我在树上找到其对应的那个结点,然后统计这个节点中有多少个标记节点?”小Ho不是很确定的答道:“但是这样…似乎在最坏情况,也就是你每次给个字符串都很短的时候,我还是要扫描这棵树的很大一部分呢?也就是说虽然平均时间复杂度降低了,但是最坏情况时间复杂度还是很高的样子!”
小Hi笑嘻嘻道:”没想到你自己看出来了呢~我还以为又要教训你了!~那你有什么好的解决方法么?”
“没呢!小Hi你就别卖关子了,赶紧告诉我吧!”被折磨的够呛的小Ho开始求饶。
“好吧!就帮你这一回~”
“小Ho你有没有想过这样一个问题?不妨称以T为根的子树中标记节点的个数为L[T],既然我要统计某个L[T1],,而这个结点是不确定的,我有没有办法一次性把所有结点的L[T]求出来呢?”小Hi整理了下思绪,问道。
“似乎是有的,老师以前说过,递归什么的。。”小Ho答道。
“递归太复杂了!我们可以之后再说,你这么想,在你构建Trie树的时候,当你经过一个结点的时候,说明了什么?”小Hi撇了撇头,继续问道。
“我想想,经过一个结点……标记结点……说明了以这个结点为根的子树中将要多出来一个标记结点?”
“没错!那你有没有什么办法来记录这个改变呢?”
“我想想,我在最开始置所有L[T]=0,然后每次添加一个新的单词的时候,都将它经过的所有结点的L[T]全部+1,这样我构建完这棵Trie树的时候,我也就能够同时统计到所有L[T]了,对么?”小Ho开心道。
“那么现在!赶紧去用代码实现吧!”小Hi如是说道
输入
输入的第一行为一个正整数n,表示词典的大小,其后n行,每一行一个单词(不保证是英文单词,也有可能是火星文单词哦),单词由不超过10个的小写英文字母组成,可能存在相同的单词,此时应将其视作不同的单词。接下来的一行为一个正整数m,表示小Hi询问的次数,其后m行,每一行一个字符串,该字符串由不超过10个的小写英文字母组成,表示小Hi的一个询问。
在20%的数据中n, m<=10,词典的字母表大小<=2.
在60%的数据中n, m<=1000,词典的字母表大小<=5.
在100%的数据中n, m<=100000,词典的字母表大小<=26.
本题按通过的数据量排名哦~
输出
对于小Hi的每一个询问,输出一个整数Ans,表示词典中以小Hi给出的字符串为前缀的单词的个数。
样例输入
5
babaab
babbbaaaa
abba
aaaaabaa
babaababb
5
babb
baabaaa
bab
bb
bbabbaab
样例输出
1
0
3
0
0
数据结构:
private class TrieNode{
private int num;
private Map<Character,TrieNode> sons;
private boolean isEnd;
TrieNode(){
num=0;
sons = new HashMap<Character,TrieNode>();
isEnd = false;
}
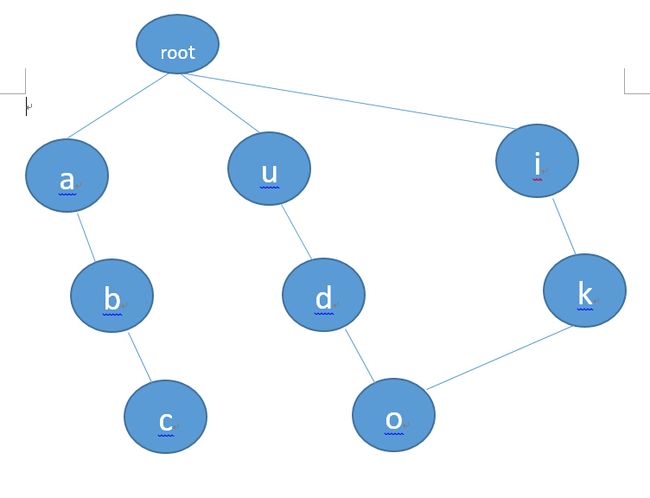
}实现思想:通过HashMap<Character,TrieNode>()实现,将同层的节点分配,例如说:{“abc”,”udo”,”ikn”}这三个单词,属于同层的是每个单词的第一个字母,”abc”中的”a”,”udo”中的”u”,”ikn”中的”i”。
将上述三个词进行hashmap操作可得类似如下示意图:
以下是实现代码:
TrieTree类成员:
private TrieNode root;节点结构:
private class TrieNode{
private int num;//记录频数
private Map<Character,TrieNode> sons;//节点结构
private boolean isEnd;//结束标志
//初始化节点
TrieNode(){
num=0;
sons = new HashMap<Character,TrieNode>();
isEnd = false;
}
}构造函数:
TrieTree(){ root = new TrieNode(); }节点插入:
public void insert(String word){
//字符非正常
if(word.length()<=0||word==null)
return;
TrieNode node = root ;
for(int i = 0 ; i<word.length();i++){
//map中不含有该字符,则分配一个新的节点
if(!(node.sons.containsKey(word.charAt(i)))){
node.sons.put(word.charAt(i),new TrieNode());
}
//含有该字符则频数+1
node = node.sons.get(word.charAt(i));
node.num++;
}
//标记结束
node.isEnd = true;
}前缀出现频数:
public int countPrefix(String prefix){
//非正常前缀
if(prefix.length()<=0||prefix.trim()==null)
return -1;
//正常前缀
TrieNode node = root ;
for(int i = 0 ; i < prefix.length();i++){
if(node.sons.containsKey(prefix.charAt(i))){
node = node.sons.get(prefix.charAt(i));
}else{
return 0;
}
}
//返回前缀频数
return node.num;
}主函数:
TestTrie tree = new TestTrie();
//控制台输入
Scanner input = new Scanner(System.in);
//数组大小
int num = input.nextInt();
String[] strs = new String[num];
//初始化数组
for(int i = 0 ;i < num ;i++){
strs[i] = input.next();
}
int quesnum = input.nextInt();
String[] ques = new String[quesnum];
for(int i = 0 ;i < quesnum ;i++){
ques[i] = input.next();
}
//树的插入
for(String word:strs){
tree.insert(word);
}
//打印频数
for(String pre:ques){
System.out.println(tree.countPrefix(pre));
}
}
