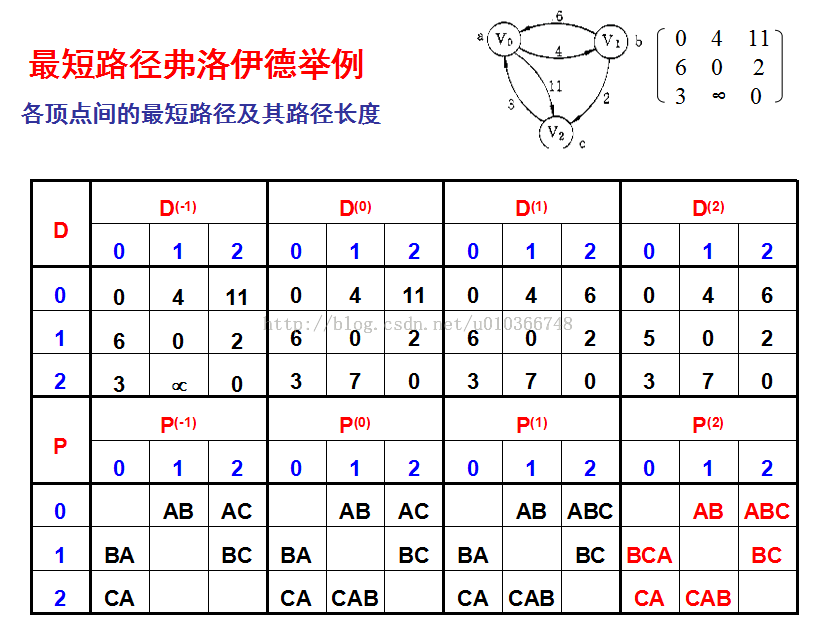
Floyd算法求解每一对顶点之间的最短路径2
已知一个各边权值均大于 0 的带权有向图,对每对顶点 vi≠vj,要求求出每一对顶点之间的最短路径和最短路径长度。
解决方案:
1.每次以一个顶点为源点,重复执行迪杰斯特拉算法n次。这样,便可求得每一对顶点之间的最短路径。总的执行时间为O(n3)。
2.形式更直接的弗洛伊德(Floyd)算法。时间复杂度也为O(n3)。
弗洛伊德算法思想:
假设求从顶点Vi到Vj的最短路径。如果从Vi到Vj有弧,则从Vi到Vj存在一条长度为arcs[i][j]的路径,该路径不一定是最短路径,尚需进行n次试探。
首先考虑路径(Vi,V0,Vj)是否存在(即判别(Vi,V0)、(V0,Vj)是否存在)。如存在,则比较(Vi,Vj)和(Vi,V0,Vj)的路径长度,取长度较短者为从 Vi到Vj 的中间顶点的序号不大于0 的最短路径。假如在路径上再增加一个顶点 V1,…依次类推。可同时求得各对顶点间的最短路径。
定义一个n阶方阵序列D(-1),D(0),D(1),D(2),......D(k),......D(n-1)
其中:
D(-1)[i][j]= arcs[i][j],其中arcs[i][j]为带权值的邻接矩阵
D(k)[i][j]=Min { D(k-1)[i][j],D(k-1)[i][k]+D(k-1)[k][j] },0≤k≤n-1
可见,D(1)[i][j]就是从vi到vj的中间顶点的序号不大于1的最短路径的长度;
D(k)[i][j]就是从vi到vj的中间顶点的序号不大于k的最短路径的长度;
D(n-1)[i][j]就是从vi到vj的最短路径的长度。
实例:
package utils;
import java.io.File;
import utils.AdjacentMatrix;
public class ShortestPath {
public static void floydShortestPath(){
/*File file = new File("D:/xj_algorithm_test_data/shortest_path_test.txt");
AdjacentMatrix.StoreInAdjacentMatrix(file);
int n = AdjacentMatrix.N;
int[][] A = AdjacentMatrix.d;//A为邻接矩阵*/
int[][] A = {//测试
{0,4,11},
{6,0,2},
{3,Global.INF,0}
};
int n = A[0].length;
int[][] dis = new int[n][n];//distance用来存储dis[i][j]从vi到vj的最短距离值
//每次加入新节点k时都会比较dis[i][j]与dis[i][k]+dis[k][j]的大小以决定是否来更新最短距离
int[][] path = new int[n][n];//path[i][j]用来存储vi到vj的最短路径之该条路径的vj的前驱结点
//说明:
//要输出vi到vj的最短路径,path[i][j]存储的最短路径的vj的前驱结点,假设为k,即kj一定在vi到vj的最短路径上:i->...->k->j,输出
//k后,再只需查看path[i][k]存储的节点即vk的前驱结点假设为h,那么vi到vj的最短路径是i->...->h->k->j,以此类推,
//最终可输出vi到vj的最短路径
for(int i =0;i<n;i++){//先做dis[][] 和path[][]的初始化工作
for(int j=0;j<n;j++){
dis[i][j] = A[i][j];
path[i][j] = i;//先假设vi到vj的直达路径,即vj的前驱就是vi
//如果i到j本来就直接可达,这么假设没有错;如果i到j直接不可达,那么后期可以通过加入其他节点而可达,
//这样dis[][]和path[][]一定会被更新,所以这里对path[][]的假设也不无妨
//当然这样假设的大前提:所有的节点之间都可以互相可达(可通过走其他节点)
//但其实如果确实存在某两节点不可达(路径值无穷大),在后面的dis[][]的更新中它依然不会被更新,因为没有中间结点使他们可达
//在最后的打印输出中由于不满足条件dis[i][j]!=Global.INF,path[][]里对应的值也不会被输出,故不会造成影响
}
}
for(int k =0;k<n;k++){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if((dis[i][k]+dis[k][j]<dis[i][j])&&(dis[i][k]!=Global.INF)&&(dis[k][j]!=Global.INF)){
dis[i][j] = dis[i][k]+dis[k][j];
path[i][j] = path[k][j];//注意这里不要迷惑,ij路径上j的前驱被指为path[k][j],不要认为path[i][j]就等于了k,即
//不要误认为此时j的前驱就是k了,
//注意这里是path[k][j]而不是k,所以path[k][j]的值有可能是k,还有可能是kj路径上存在的其他节点h,此节点h是该路径上j的前驱
//即以前的i->....->j变为现在的i->...->k->...->j,而不是i->...->k->j而产生担心顾虑,后者是前者的某一种情况而已
//例如:没加入k时有i->...->j,k->...->h->j
//加入k节点后路径i->...->k->...j更短了,那么此时path[i][j]=path[k][j]=h
}
}
}
}
for(int i=0;i<n;i++){//打印最短路径//打印路径i->...->j,先从j打印,再根据path[][]打印j的前驱,再打印前驱的前驱...
for(int j=0;j<n;j++){
if((i!=j)&&(dis[i][j]!=Global.INF)){//dis[i][j]!=Global.INF就可以避免输出那些相互不可达的点对的path[][]值
//因为path[][]里即使存了数据,由于不可达,此时也不会输出
System.out.println();
System.out.println("v"+i+"到v"+j+"的最短距离为:"+dis[i][j]);
System.out.println("v"+i+"到v"+j+"的最短路径为:");
//路径的第一种输出方式,k=j,ij的最短路径先输出k,在输出k的前驱再输出前驱的前驱...直到k == i,即逆向输出
int k = j;
while(k!=i){
System.out.print(k+"<-");
k=path[i][k];
}
System.out.print(i);
//路径的第二种输出方式,先输出i->j,k1 = j的前驱,输出i->k1->j,k1在给出前驱的前驱设为h,则输出i->h->k->j
//每次插入新加入的前驱结点构成最短路径串
int k1 = path[i][j];
String tmpStr = "" + j;
String pathStr = "" + i + "->" + j;
while(k1!=i){
tmpStr = k1 + "->" + tmpStr ;
pathStr = i + "->" + tmpStr ;
k1=path[i][k1];
}
System.out.println();
System.out.println(pathStr);
//路径的第三种输出方式,思路与第二种完全能想同,只是数字对应的节点标识符:如v0:A,v1:B,v2:C......
char[] charPath = {'A','B','C'};
//int pathNodesNum = 0;
int k2 = path[i][j];
String tmpStr2 = "" + charPath[j];
String pathStr2 = "" + charPath[i] + "->" + charPath[j];
while(k2!=i){
tmpStr2 = charPath[k2] + "->" + tmpStr2 ;
pathStr2 = charPath[i] + "->" + tmpStr2 ;
k2=path[i][k2];
//pathNodesNum++;
}
//System.out.println();
System.out.println(pathStr2);
//char[] charPath = new char[pathNodesNum];
}
}
}
}
public static void main(String[] args) {
floydShortestPath();
}
}
测试结果: