算法基础——经典八大排序算法的Java及Python实现
概述
代码
以下是经典八大排序算法的Java及Python代码,都是基于经典算法书籍《算法导论》里的伪代码实现的,我在关键语句部分附上了注释。
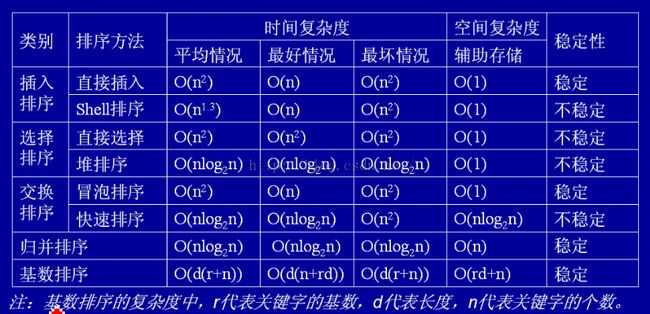
按照上图中的顺序分别介绍八大排序算法的实现(升序),前面是Java,后面是Python。Java的排序函数写在了一个类里,Python的排序函数则直接写出来了。
直接插入排序
public class InsertSort {
//插入排序,最好情况O(n),最坏情况O(n^2),稳定原址排序
public int[] Sort(int[] arr){
for(int i=0;i<arr.length;i++){
int key = arr[i];
int j = i-1;
for(;j>=0 && arr[j]>key;j--)
arr[j+1] = arr[j];//注意!这里不是交换,而是把比key大的都往后挪
arr[j+1] = key;//key再插入合适的位置
}
return arr;
}
}
def insertSort(arr):
#插入排序,最坏为O(n^2),最好为O(n)
#升序排列一个数组,降序排列将while语句中改为arr[i]<key即可
if(arr==None or len(arr)<2):
return arr
for j in range(1,len(arr)):
key = arr[j]#待插入的数
i = j-1
while(i>=0 and arr[i]>key):
#从后往前比较待插入的数和当前数,将arr[j-1]、arr[j-2]...向右移动直到找到arr[j]的适当位置
arr[i+1] = arr[i]
i -= 1
arr[i+1] = key#遍历完将arr[j]插入到该位置
return arr
希尔排序
public class ShellSort {
// 希尔排序,最好情况O(n),最坏情况O(n^2),平均情况比直接插入排序要好,平均情况为O(n^1.3)
//不稳定,原址排序
public int[] Sort(int[] arr) {
int n = arr.length;
for (int gap = n; gap > 0; gap/=2) {
for (int i = gap;i < n;i++){
if (arr[i] < arr[i-gap]){//如果比前面的元素小,则以步长为gap进行插入排序
int key = arr[i];
int j = i-gap;
while (j>=0 && arr[j] > key){
arr[j+gap] = arr[j];
j -= gap;
}
arr[j+gap] = key;
}
}
}
return arr;
}
}
def shellSort(arr):
#改进版的插入排序-希尔排序,最坏为O(n^2),最好为O(n),平均为O(n^1.3)
gap = len(arr)/2
while gap > 0:
for i in range(gap,len(arr)):
if arr[i] < arr[i-gap]:#后面的元素比前面的小,以gap为步长进行插入排序
key = arr[i]
j = i - gap
while j>=0 and arr[j]>key:
arr[j+gap] = arr[j]
j -= gap
arr[j+gap] = key
#步长减一半
gap /= 2
return arr
直接选择排序
public class SelectSort {
//选择排序,最坏和最好都为O(n^2),不稳定,原址排序
public int[] Sort(int[] arr) {
int n = arr.length;
if (n<2)
return arr;
for(int i=0;i<n-1;i++){
int index = i;
for(int j=i+1;j<n;j++){
if(arr[j]<arr[index]){
index = j;//找出剩余元素中最小那个数的下标
}
}
//将剩余元素中最小那个数跟当前数交换
int tmp = arr[i];
arr[i] = arr[index];
arr[index] = tmp;
}
return arr;
}
}
def selectSort(arr):
#选择排序,最坏为O(n^2)
#升序排列一个数组,降序排列将while语句中改为arr[i]<key即可
if(arr==None or len(arr)<2):
return arr
for j in range(len(arr)):
index = j
for i in range(j,len(arr)):
if arr[i] < arr[index]:
index = i#找出剩余的最小元素
#未排序中最小的元素跟arr[j]交换
tmp = arr[j]
arr[j] = arr[index]
arr[index] = tmp
return arr
堆排序
public class HeapSort {
//维护一个最大堆,使其以i节点的元素为根
public void maxHeapify(int[] arr,int i,int heap_size){
int l = 2*i+1;//左孩子节点
int r = l+1;
int largest = i;
if(l<heap_size && arr[l]>arr[largest])
largest = l;
if(r<heap_size && arr[r]>arr[largest])
largest = r;
if(largest != i){
//保证i节点为最大,并维护以largest节点为根的最大堆
int tmp = arr[i];
arr[i] = arr[largest];
arr[largest] = tmp;
maxHeapify(arr,largest,heap_size);
}
}
public void buildMaxHeap(int[] arr){
int heap_size = arr.length;
int mid = (heap_size-1)/2;
//从中间节点开始把arr建为最大堆(只需遍历数组的一半),最后使得arr[0]为最大堆的根
for(int i=mid;i>=0;i--)
maxHeapify(arr,i,heap_size);
}
public int[] Sort(int[] arr){
//先把数组建造为最大堆
buildMaxHeap(arr);
//从后往前遍历,根据最大堆的性质arr[0]最大
for(int i = arr.length-1;i>=0;i--){
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
int heap_size = i;
maxHeapify(arr,0,heap_size);
}
return arr;
}
}
def maxHeapify(arr,i,heap_size):
#维护一个最大堆,让arr[i]的值在最大堆中逐级下降,使得以i为根节点的子树是最大堆,O(lgn)
l = 2*i+1#下标i从0开始,因此左孩子节点的下标是2*i+1
r = l + 1#右孩子节点
largest = i
if l<heap_size and arr[l]>arr[largest]:#注意heap_size初始化为len(arr),这里判断应为l<heap_size
largest = l
if r<heap_size and arr[r]>arr[largest]:
largest = r
if largest != i:#i不是最大堆的根节点,就交换值,并且让largest为根节点的子树保持最大堆
arr[largest],arr[i] = arr[i],arr[largest]
maxHeapify(arr,largest,heap_size)
def buildMaxHeap(arr):
#自顶向上,将arr转换为最大堆
heap_size = len(arr)
mid = int((heap_size-1)/2)
for i in range(mid,-1,-1):
maxHeapify(arr,i,heap_size)
def heapSort(arr):
buildMaxHeap(arr)#时间复杂度O(n)
size = len(arr)
#n-1次调用maxHeapify,时间复杂度O(nlgn)
for i in range(size-1,-1,-1):
arr[i],arr[0] = arr[0],arr[i]#从后往前存储,根据最大堆性质,arr[0]是当前最大堆的最大值
heap_size = i
maxHeapify(arr,0,heap_size)
冒泡排序
public class PopSort {
public int[] Sort(int[] arr) {
int n = arr.length;
if(n<2)
return arr;
for(int i=0;i<n;i++)
for(int j=n-1;j>i;j--){
if(arr[j-1]>arr[j]){
int tmp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = tmp;
}
}
return arr;
}
}
def popSort(arr):
n = len(arr)
if n < 2:
return arr
for i in range(n):
for j in range(n-1,i,-1):
if arr[j-1] > arr[j]:
arr[j-1],arr[j] = arr[j],arr[j-1]
return arr
快速排序
public class QuickSort {
public int getPartition(int[] arr,int low,int high){
int tmp;
int index = low - 1;
for(int i = low;i<high;i++){
//arr[index]及其以前的都比arr[high]小
if(arr[i]<=arr[high]){
index++;
tmp = arr[i];
arr[i] = arr[index];
arr[index] = tmp;
}
}
//把arr[high]放到合适位置
tmp = arr[index+1];
arr[index+1] = arr[high];
arr[high] = tmp;
return index+1;
}
public void Sort(int[] arr,int low,int high) {
//选一个基准元素将arr分成左边小右边大的两部分,注意high是最大下标
if(low<high){
int mid = getPartition(arr,low,high);
Sort(arr,low,mid-1);
Sort(arr,mid+1,high);
}
}
}
def quickSort(arr,low,high):
#随机选择基准元素的快速排序,达到期望时间复杂度O(nlgn)
#注意high是最大下标
if low < high:
mid = getPartition(arr,low,high)
#对基准元素两边的数组快排
quickSort(arr,low,mid-1)
quickSort(arr,mid+1,high)
def getPartition(arr,low,high):
#随机选择一个数并与arr[high]交换,防止最坏情况
#将arr[high]作为基准进行排序
rand = random.randint(low,high)
arr[high],arr[rand] = arr[rand],arr[high]
index = low - 1
for i in range(low,high):
if arr[i] <= arr[high]:#保证index前面的数都比key小
index += 1
arr[index],arr[i] = arr[i],arr[index]
arr[index+1],arr[high] = arr[high],arr[index+1]
return index+1
归并排序
public class MergeSort {
public void Sort(int[] arr,int low,int high){
if(low<high){
//注意high是最大下标
int mid = (int)((low+high)/2);
Sort(arr,low,mid);
Sort(arr,mid+1,high);
mergeArr(arr,low,mid,high);
}
}
public void mergeArr(int[] arr,int low,int mid,int high){
int n1 = mid-low+1;//注意左边数组的长度
int n2 = high-mid;
int[] arr1 = new int[n1+1];
int[] arr2 = new int[n2+1];
int i = 0;
int j = 0;
//把mid左右两边的数分别放在两个数组里
for(;i<n1;i++)
arr1[i] = arr[low+i];
for(;j<n2;j++)
arr2[j] = arr[mid+1+j];
//放置无穷大的值作为哨兵值,简化边界处理
arr1[n1] = Integer.MAX_VALUE;
arr2[n2] = Integer.MAX_VALUE;
i = 0;
j = 0;
for(int k=low;k<=high;k++){
//比较左右两个数组的元素,将小的依次放入arr[k]
if(arr1[i]<=arr2[j]){
arr[k] = arr1[i];
i++;
}
else{
arr[k] = arr2[j];
j++;
}
}
}
}
def mergeSort(arr,p,r):
#p17,归并排序,O(nlgn).注意r是数组的最大下标
if p<r:
q = int((p+r)/2)
mergeSort(arr,p,q)
mergeSort(arr,q+1,r)
Merge(arr,p,q,r)
def Merge(arr,p,q,r):
#合并两个有序数组,arr1[p...q]和arr2[q+1...r]
n1 = q-p+1#左边数组的长度(因为q中位数是向下取整,所以q-p+1)
n2 = r-q#右边数组的长度
arr1 = []
arr2 = []
for i in range(n1):
arr1.append(arr[p+i])
for j in range(n2):
#注意j的范围
arr2.append(arr[q+1+j])
arr1.append(float('inf'))#放置一个无穷大的数作为“哨兵值”
arr2.append(float('inf'))
#print(arr1,arr2)
i,j = 0,0
for k in range(p,r+1):#注意k的范围
if arr1[i] <= arr2[j]:
arr[k] = arr1[i]
i += 1
else:
arr[k] = arr2[j]
j += 1
基数排序
这个用Java写太麻烦了,各种麻烦的ArrayList操作~~所以只贴Python版def cntDigit(arr,radix):
#获取数组元素的最大位数
maxnum = arr[0]
for x in arr:
if x > maxnum:
maxnum = x
cnt = 0
while(maxnum != 0):
maxnum /= radix
cnt += 1
return cnt
def radixSort(arr,radix=10):
k = cntDigit(arr,radix)#获取最大位数
bucket = [[] for i in range(radix)]
for i in range(1,k+1):
for j in arr:
#bucket[x]存储从低到高第i位为x的数,如数组中的543,i=1时存在bucket[3]里
bucket[j/(radix**(i-1)) % (radix)].append(j)
del arr[:]#先初始化arr
#print(bucket)
for z in bucket:#当前位数的数组按顺序放入arr中
arr += z
del z[:]
return arr