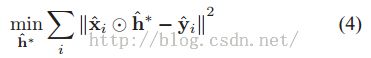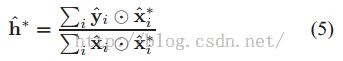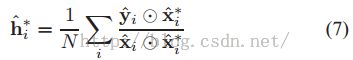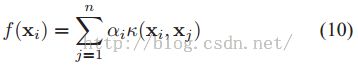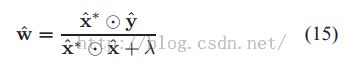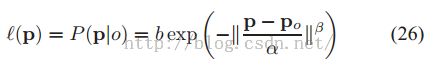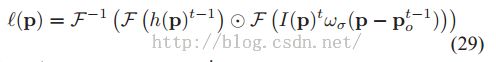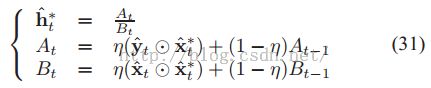An Experimental Survey on Correlation Filter-based Tracking
An Experimental Survey on Correlation Filter-based Tracking
本文参考文章《An Experimental Survey on Correlation Filter-based Tracking》
这篇文章中,作者对近年来基于相关滤波方法的视觉跟踪的有关研究进行了总结。作者通过一个统一的框架,总结了11种方法,回顾了这些算法的贡献,图表1做出了总结。
一般来说,滤波器的训练机制对于基于相关滤波跟踪的算法来说是相当重要的。相关滤波器方法大致可以从以下几个方面改进:(1)更好的训练机制、(2)提取更好的特征、(3)减轻尺度变化带来的问题、(4)采用基于块的跟踪策略、(5)采用长期跟踪。
一、基于相关滤波的跟踪框架
根据已有的相关滤波算法,一般的工作框架可以总结如下(图1):
(1)相关滤波器是根据从视频的第一帧中目标位置提取的图像块中训练、学习得到的;
(2)对于随后的每一帧,从上一帧目标位置的区域提取图像块用来检测;
(3)可以从原始的输入数据中提取大量特征,通常情况下,为了平滑结果,我们会加上一个cosine window;
(4)我们利用余弦傅里叶变换类替代卷积操作,会使计算效率大幅提升;
(5)通过傅里叶变换之后,我们会得到响应图谱,具有最大响应值的位置就是我们要预测的目标的位置;
(6)提取估计位置的目标的外观,用来训练和更新相关滤波器。
用数学语言表述如下:
我们让X表示输入,h表示相关滤波器。在实际任务中,X可以是原始的图像块,也可以是提取的特征。假设^表示的是一个向量的傅里叶变换。根据卷积定理,循环卷积等于频域的元素之间的乘积:
训练滤波器时,我们首先定义一个期望的相关输出y。然后用目标的实例和相关滤波器来满足如下式子:
解这个式子,我们可以得到:
通过转到频域计算,对于一个n*n大小的图像块,计算复杂度会由
![]() 下降到
下降到
![]()
 。我们可以看到这个加速效果是非常的显著的。
。我们可以看到这个加速效果是非常的显著的。
二、相关滤波的训练机制
A、传统的训练方法
最简单的情况,从一个图像上截取一个模板,用它来对于目标产生顶峰。但是这种方法有时候对于背景也会产生一个很高的响应。为了解决这个问题,一些方法通过抑制负样本的响应,保留正样本的响应来训练。但是这种硬性的约束有时候并不能取得一个良好的效果。有一种叫做平均所有的滤波器(ASEF)的方法,通过平均所有训练得到的滤波器来得到一个一般的滤波器。尽管这种方法取得了不错的效果,但是他需要大规模的样本用来训练,这就制约了它的跟踪速度。
B、适应性的相关滤波
MOSSE(最小均方误差和输出)方法在ASEF的基础上做出了一些改进,提高了效率。
1)、MOSSE:根据上面公式(2)(3)我们可以很容易的计算出相关滤波器。因为这样得到的滤波器不够鲁棒,所以需要大量的训练样本,为了更好的将这些训练样本映射到他们期望的输出,MOSSE方法通过最小化这些样本的真实值与期望输出值的均方误差和,得到相关滤波器h。这个计算转化到频域,计算方式如下:
i表示的是每一个训练样本的索引。通过解这个式子可以得到:
2)、Regularized ASEF:通过稍微改变原始的形式,ASEF也可以应用到有效的跟踪中。每次只用一个样本,通过公式(4)得到一个滤波器:
然后通过计算所有的滤波器的平均值的方式得到一个更一般的滤波器:
但是,原始的ASEF是不稳定的,因为公式(7)中的分母可能会特别小。通常在应用的时候,为了使系统更加稳定,可以在分母上加上一个正则项。
C、核相关滤波
所有基于上述方法的性能会有一定的限制,因为ASEF和MOSSE滤波器可以被看做是一个简单的线性分类器。通过使用核函数,可以是相关滤波方法的性能更好。
一些算法提出,相关滤波可以通过引进脊回归问题和循环矩阵来有效的利用核。
1)、Ridge Regression Problem:通过将相关滤波器看作是一个分类器,我们可以通过找到第i个训练样本和他对应的标签之间的关系来训练。我们假设他们的关系是通过这样一个函数式得到的,训练问题可以看做是最小化如下这样一个目标函数:
w表示的是参数。
![]() 是正则化参数,为了阻止过拟合。
是正则化参数,为了阻止过拟合。
![]() 是损失函数。
是损失函数。
对于函数
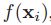
![]() ,它可以是一个线性操作。通过求解上面的公式(8),w可以通过一个闭解的形式得到:
,它可以是一个线性操作。通过求解上面的公式(8),w可以通过一个闭解的形式得到:
X表示的是一个矩阵,他的每一行代表一个训练样本,y表示的对应样本的标签,I是单位矩阵。值得注意的是,如果要是在频域计算的话,
![]()
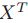 应该用他的
厄密矩阵替换,即
应该用他的
厄密矩阵替换,即
![]()
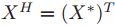 。
。
为了引入核函数来提高性能,输入数据可以通过
![]() 映射到一个非线性的特征空间中,这样w就可以通过输入的线性组合来表示
映射到一个非线性的特征空间中,这样w就可以通过输入的线性组合来表示
![]()
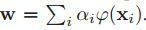 。然后
。然后

![]() 就变成了如下的形式:
就变成了如下的形式:
为了减少公式(11)中求矩阵逆运算的复杂度,我们引入了循环矩阵。
2)、Circulant Matrix:一般情况下我们都是通过随机采样获取样本的。但是,通过使用循环矩阵,我们可以非常容易的在目标的周围获取训练样本而不会牺牲速度。
对于一个样本
![]()
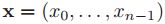 ,我们可以得到一个循环矩阵X,如下所示:
,我们可以得到一个循环矩阵X,如下所示:
循环矩阵有很多有趣的性能,比如,他们的和、乘积以及逆运算也都是循环行列式。此外,一个循环矩阵可以用它的基准向量的离散傅里叶变换对角化:
F是离散傅里叶变化矩阵,它是用来计算一个向量
![]() 的离散傅里叶变换。这样一来w的解就可以表述为如下这种形式:
的离散傅里叶变换。这样一来w的解就可以表述为如下这种形式:
它可以用频域上一个更加简单的形式表示如下:
这个除法操作是元素级的。同样的,如果核矩阵K也是一个循环矩阵的话,
![]() 也可以通过如下式子有效的计算:
也可以通过如下式子有效的计算:
k是循环矩阵K的基准向量,同样,可以得到:
3)、Detection:对于新来的一帧,我们可以通过训练得到的参数
![]()
 和一个基准样本x来检测得到。如果新样本是z,那么置信图可以通过如下式子得到:
和一个基准样本x来检测得到。如果新样本是z,那么置信图可以通过如下式子得到:
和ASEF、MOSSE方法一样,y值最大的位置就是目标的位置。
D、密集时空上下文跟踪器
替代训练优化问题,STC设计学习一个似然分布,它被定义为目标定位在位置
![]()
 的先验概率:
的先验概率:
让
![]()
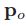 表示目标中心的位置。
表示目标中心的位置。
![]() 表示的是
表示的是
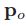
![]() 周围的区域。于是上下文信息就可以通过
周围的区域。于是上下文信息就可以通过
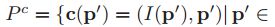
![]()
![]() 来定义。
来定义。

![]() 表示的是
表示的是
![]() 处的图片的强度。通过计算
处的图片的强度。通过计算

![]() 的边缘概率分布,得到:
的边缘概率分布,得到:
因为没有对
![]() 的直接表达,所以我们定义了如下的式子来表述:
的直接表达,所以我们定义了如下的式子来表述:
h可以是一些计算两个输入向量(
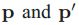
![]() )
之间差异的操作。为了去除周围相似目标的干扰,h应该不是径相对称的,简而言之,
)
之间差异的操作。为了去除周围相似目标的干扰,h应该不是径相对称的,简而言之,
![]()
 应该是不相等的。
应该是不相等的。
对于
![]() ,可以定义如下:
,可以定义如下:
为了训练
![]()
 ,期望输出分布
,期望输出分布
![]() 可以通过手工设计。如果知道目标是在场景的中间,
可以通过手工设计。如果知道目标是在场景的中间,
![]() 可以被定义为如下形式:
可以被定义为如下形式:
b也是正则化参数,
![]()
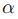 是尺度参数,
是尺度参数,
![]()
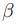 控制着分布的形状。接下来,联合上面的式子可以得到:
控制着分布的形状。接下来,联合上面的式子可以得到:
通过引进卷积定理,我们得到:
这样就可以得到训练的
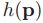
![]() ,对于新来一帧图像,
,对于新来一帧图像,
![]()
 可以通过下面的式子计算得到:
可以通过下面的式子计算得到:
同样的,
![]()
 最大值的位置就是目标的新的位置。
最大值的位置就是目标的新的位置。
E、更新机制
根据上面介绍的训练机制,每一帧都会产生一个相关滤波器,因此将它和之前训练好的滤波器合并对于我们得到一个鲁棒的外观模型是非常的重要的。
对于一个正则化的ASEF,一个一般的相关滤波器更新是通过平均所有学习到的滤波器,计算形式如下:
MOSSE是通过分别平均分子、分母来更新的,计算形式如下:
KCF,双重空间系数
 可以在频域更新,计算形式如下:
可以在频域更新,计算形式如下:
z表示的从当前预测位置上的采样。
鲁棒的更新机制也要通过考虑长期更新来实现。如果一个目标丢失或者是被遮挡,学习他的外观模型是有害的。为了避免学习误判的样本,一些人引进了长期跟踪组件。比如,当检测到有遮挡时,就停止更新;如果长期跟踪组件具有更高的置信度,我们就重新刷新我们的相关滤波器。
F、比较不同的训练机制
对于ASEF,他的滤波器的产生是通过平均所有学习到的滤波器,但是MOSSE的滤波器则是通过平均所有的图像训练的到的。通过引入脊回归问题和循环矩阵,核相关滤波器等。STC和他们则有很多不同的地方:(1)STC建立了目标及其上下文之间的关系,但是其他相关滤波跟踪方法则用训练的额滤波器建模输入的外观;(2)STC得到的置信图可以看做是给定的当前目标的先验概率,但是其他跟踪算法的置信图的值表示的是相关分数;(3)STC可以进行任意尺度的估计,但是这一点对于其他跟踪还是很困难的。