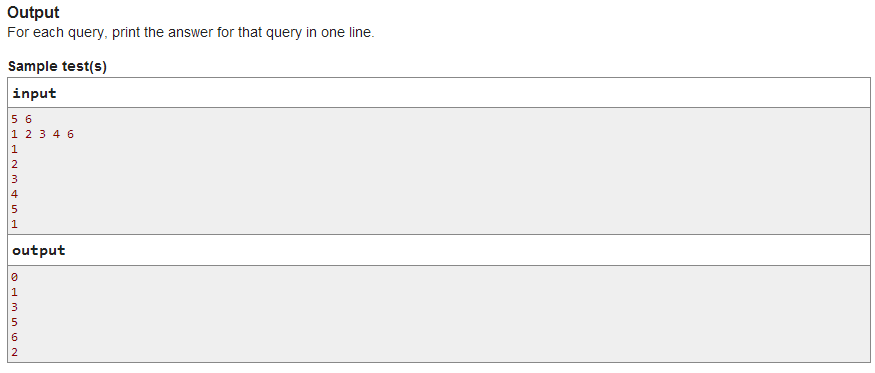
CodeForces 547C. Mike and Foam 莫比乌斯反演
题意:给定一个长度为n的数列a,和q个操作(1<= n,q <= 2*10^5, 1 <= a[i] <= 5*10^5 )
需要维护一个多重集合Q.
每个操作给出一个下标i,如果a[i]属于Q那么把a[i]从Q中拿走,如果a[i]不属于Q,那么把a[i]加入Q中。
每次操作后询问Q中,有多少对i,j满足条件 i<j 且 gcd(a[i],a[j])=1
这个性质的维护比较困难,直接做是O(n*q)
答案是利用莫比乌斯反演定理来做:
d[k]表示集合Q中,有多少个元素是k的倍数
本题中d <= 5*10^5,因为当d>5*10^5时,所有的F(d)都一定为0
现在直接来看最后K的公式,增减元素之后,只要调整所有影响的F值,就可以得到新的K值。
然后关于莫比乌斯函数u(x),当x含有任何质数因子的平方或更高次方的时候u(d)=0,所以这时的F的变化不用考虑。
2*3*5*7*11*13*17=510510>5*10^5,所以本题中,任何的a[i]最多含有6个不同的质因子。
那么a[i]的因子d 中,使u(d) != 0 的最多只有2^6 =64个
于是如果要加入或删除某个a[i] ,只需找到a[i]影响的最多64个d[i],根据d[i]来调整K值就行了。
总复杂度O(q * 64)
在代码中,没有记录F[i],只记录了d[i],然后根据d[i]的变化来调整K.
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#define maxn 200007
#define maxv 500007
using namespace std;
int maxprime[maxv];/* maxprime[i]是i的质因数中最大的一个 */
int u[maxv];/* 莫比乌斯函数 */
bool On[maxn];/* 记录a[i]是否在集合内 */
int d[maxv];/* 记录d[k]表示集合内有多少个值是k的倍数 */
int a[maxn];
int n,q;
long long K;
void Init(){/* 初始化maxprime和u数组 */
memset(maxprime,-1,sizeof(maxprime));
for(int i=1;i<maxv;++i) u[i]=1;
for(int i=2;i<maxv;++i){
if(~maxprime[i]) continue;
for(int j=1,v=i;v<maxv;++j,v+=i){
maxprime[v]=i;
u[v]=j%i==0?0:-u[v];
}
}
}
bool Add(int x){/* 加入x */
int fac[6],facn=0;
while(x>1){/* 质因数分解 */
int p=maxprime[x];
fac[facn++]=p;
do x/=p;
while(x%p==0);
}
int MAX=1<<facn;
for(int i=0;i<MAX;++i){/* 调整所有的d值以及K值 */
int t=i,v=1;
for(int j=0;j<facn;++j,t>>=1){
if(t&1) v*=fac[j];
}
K+=d[v]*u[v];
++d[v];
}
return true;
}
bool Remove(int x){/* 删除x */
int fac[6],facn=0;
while(x>1){/* 质因数分解 */
int p=maxprime[x];
fac[facn++]=p;
do x/=p;
while(x%p==0);
}
int MAX=1<<facn;
for(int i=0;i<MAX;++i){/* 调整所有的d值以及K值 */
int t=i,v=1;
for(int j=0;j<facn;++j,t>>=1){
if(t&1) v*=fac[j];
}
--d[v];
K-=d[v]*u[v];
}
return true;
}
int main(void)
{
Init();
freopen("547C.txt","r",stdin);
while(~scanf("%d%d",&n,&q)){
memset(On,0,sizeof(On));//On数组,表示a[i]是否在集合中
memset(d,0,sizeof(d));//d[k]表示集合中有多少个是k的倍数
K=0;
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=0;i<q;++i){
int x;scanf("%d",&x);
On[x]=On[x]?Remove(a[x]),false:Add(a[x]),true;
printf("%I64d\n",K);
}
}
return 0;
}