算法导论之红黑树的学习
最近学习了二叉搜索树中的红黑树,感觉收获颇丰,在此写一篇文章小结一下学到的知识,顺便手写一下Java代码。
1.引言
先来讲讲什么是二叉搜索树,二叉搜索树有如下特点:他是以一颗二叉树(最多有两个子结点)来组织的,对于树中的某个节点,其左子树的所有元素均小于该节点,其右子树的元素均大于该节点。我们知道一颗有N个节点的二叉树的高度至少为lgN,然后在树上的操作都与其高度有关,因此限制树的高度就显得非常有必要。当一个二叉搜索树的高度是lgN时,在该树上的插入删除搜索等操作均为O(lgN)的时间复杂度,但当二叉搜索树不小心插入成了链表,高度为N的时候,在树上的操作就变为O(N)了。因此我们有许多种平衡二叉树通过特定的方法来限制树的高度,红黑树就是其中的一种。红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,它在每个节点上增加了一个存储位来表示节点的颜色,可以为红色或黑色。通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因此是近似于平衡的。
2.红黑树的性质
一颗红黑树是满足以下红黑性质的二叉搜索树:
- 每个节点是红色或黑色
- 根是黑色
- 叶节点(null)是黑色的
- 红色的节点的两个子结点均为黑色
- 对于每个节点,从该节点到其所有后代的简单路径上,均包含相同数目的黑色节点(我们把到叶节点的黑色节点数称为黑高)
Java中树的节点类如下:
// 颜色枚举
enum RBColor {
RED, BLACK;
}
// 树节点类
class RBTreeNode {
RBTreeNode p = nullNode; // 父节点
RBTreeNode left = nullNode; // 左子节点
RBTreeNode right = nullNode; // 右子节点
int val; // 值
RBColor color; // 颜色
public RBTreeNode() {};
RBTreeNode(int val) {
this.val = val;
}
@Override
public String toString() {
return " (" + val + " " + color + ") ";
}
// 用于表示空叶节点的静态变量
public static RBTreeNode nullNode = new RBTreeNode() {
{
color = RBColor.BLACK; // 叶结点为黑色
}
@Override
public String toString() {
return " (null " + color + ") ";
}
};
}
3.旋转
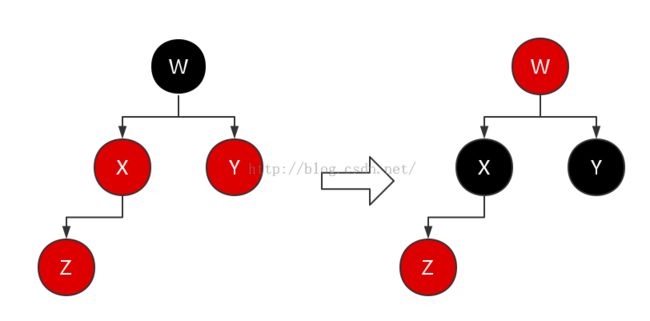
红黑树的关键操作在于其插入和删除操作,但在讲解这两步关键操作之前,我们得定义一些辅助方法来让我们更好的完成任务,该辅助方法就是树的旋转,示意图如下:
旋转由两种,分别是左旋和右旋,相信上图已经表示的非常明确,这里就不再细说,值得注意的是:在旋转操作中只有指针的改变,其他属性都保持不变。对旋转前后的树使用中序遍历将得到相同的结果。
下面是旋转的Java代码:
/**
* 左旋操作
* @param root 根结点引用
* @param node 旋转的节点
* @return 根节点
*/
public static RBTreeNode leftRotate(RBTreeNode root, RBTreeNode node) {
if (node.right == RBTreeNode.nullNode)
return root; // 左旋需要拥有右节点
RBTreeNode right = node.right;
// 旋转节点的右子树变为右节点的左子树
node.right = right.left;
if (node.right != RBTreeNode.nullNode)
node.right.p = node;
// 用右节点代替旋转节点位置
if (node.p != RBTreeNode.nullNode) {
right.p = node.p;
if (node.p.left == node)
node.p.left = right;
else
node.p.right = right;
} else {
root = right; // 没有父节点的节点为根结点
root.p = RBTreeNode.nullNode;
}
// 右节点的左子树变为旋转节点
right.left = node;
node.p = right;
return root;
}
/**
* 右旋操作
* @param root 根结点引用
* @param node 旋转节点
* @return 根节点
*/
public static RBTreeNode rightRotate(RBTreeNode root, RBTreeNode node) {
if (node.left == RBTreeNode.nullNode)
return root; // 右旋需要有左节点
RBTreeNode left = node.left;
// 旋转节点的左子树变为左节点的右子树
node.left = left.right;
if (node.left != RBTreeNode.nullNode)
node.left.p = node;
// 用左节点代替旋转节点
if (node.p != RBTreeNode.nullNode) {
left.p = node.p;
if (node.p.left == node)
node.p.left = left;
else
node.p.right = left;
} else {
root = left;
root.p = RBTreeNode.nullNode;
}
// 左节点的右子树变为旋转节点
left.right = node;
node.p = left;
return root;
}
4.插入
终于来到红黑树的第一个关键步骤了:插入操作。
对与插入操作我们利用如下思想解决:我们先把红黑树看成一个普通的二叉搜索树,对其进行插入操作,插入完成后,我们把新加入的节点染成红色,此时红黑树的红黑性质被破坏,然后再通过特定的方法来维护红黑树的性质。
插入的Java代码如下:
/**
* 红黑树插入操作
* @param root 根结点引用
* @param insertNode 要插入的新节点
* @return 根节点
*/
public static RBTreeNode rbInsert(RBTreeNode root, RBTreeNode insertNode) {
RBTreeNode position = root, parent = RBTreeNode.nullNode; // position为插入位置,parent为该位置的父节点
while (position != RBTreeNode.nullNode) {
parent = position;
if (insertNode.val < position.val) // 比该节点元素小的节点应该插入其左子树
position = position.left;
else // 比该节点元素大的节点应该插入其右子树
position = position.right;
}
insertNode.p = parent;
if (parent == RBTreeNode.nullNode) // 没有父节点的节点为根结点
root = insertNode;
else if (insertNode.val < parent.val) // 插入为左节点
parent.left = insertNode;
else // 插入为右节点
parent.right = insertNode;
insertNode.color = RBColor.RED; // 把新插入的节点染成红色
return rbInsertFixup(root, insertNode); // 修复插入时红黑树性质
}
好,终于来到重点了,红黑树的插入操作前半部分与一般二叉搜索树别无二致,区别在于最后把新加入的节点染成红色和恢复红黑树性质的部分。我们先来思考一下往红黑树插入一个红节点会破坏红黑树的什么性质?首先性质1、3、5是不会受影响的,那么当我们插入的节点是红黑树的根结点时会影响性质2,根节点变成了红色,此时我们把根节点染成黑色即可。当我们插入节点的父节点是红色时会影响性质4,红色节点有一个为红色的子结点。对于以上这些影响我们分为3种情况来处理:
关键词:叔节点
下面我们假设插入的节点为z(红色),其父节点为x(红色,为祖父节点的左节点,右节点情况镜像处理即可),其叔节点为y(未知),祖父节点为w(黑色)
情况1:插入节点z的叔节点y为红色
此时的情况如图所示(下图省略了部分不关键的子树):
此时的处理方法很简单,我们只需把祖父节点的黑色“扒”下来放到父节点X和叔节点Y即可,此时对于节点Z就保持了红黑树的性质4,然而进行了此操作后我们还需要对祖父节点W进行继续遍历,因为此时祖父节点有可能违反了红黑树的性质。当我们遍历的祖父节点为根结点时,把根结点变为黑色即可。
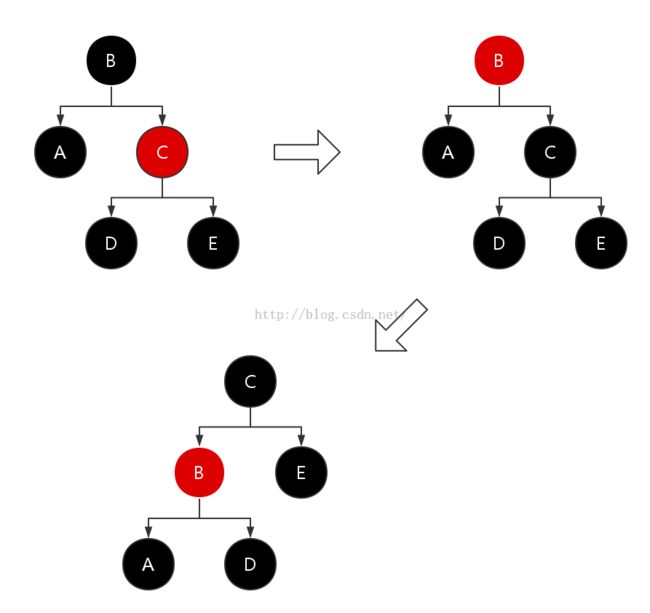
情况2:插入节点z的叔节点y是黑色的,且z是一个右孩子
左上角为情况2,此时叔节点w为黑色,且插入节点z为父节点x的右孩子,此时我们对父节点x进行一次左旋,然后交换x和z的引用,即可转换为右上角的情况3.
右上角为情况3,此时叔节点w为黑色,且插入节点z为父节点x的左孩子,此时我们进行如下操作即可恢复红黑树的性质:
- 交换父节点x和祖父节点w的颜色
- 对祖父节点w进行右旋
上面的操作既修正了对性质4的违反,也没有引起对其他红黑树性质的违反,因此我们此时可以结束对红黑树的性质修复工作。
下面给出红黑树插入时性质修复的Java代码:
/**
* 修復插入時违反的红黑树性质
* @param root 根节点引用
* @param node 修复节点
* @return 根节点
*/
public static RBTreeNode rbInsertFixup(RBTreeNode root, RBTreeNode node) {
// 修复节点不是根节点且为红色时
RBTreeNode parent = node.p, grandParent, parentBorther;
while(parent != RBTreeNode.nullNode && parent.color == RBColor.RED) {
grandParent = parent.p;
if (grandParent.left == parent) { // 父节点为左节点
parentBorther = grandParent.right; // 叔节点为右节点
if (parentBorther != RBTreeNode.nullNode && parentBorther.color == RBColor.RED) { // case 1
grandParent.color = RBColor.RED; // 祖父节点改为红色
parent.color = RBColor.BLACK; // 父节点和叔节点改为黑色
parentBorther.color = RBColor.BLACK;
node = grandParent; // 对祖父节点继续遍历
} else {
if (parent.right == node) { // case 2
root = leftRotate(root, parent); // 对父节点左旋
// 交换node和parent的引用
RBTreeNode temp = node;
node = parent;
parent = temp;
}
// case 3
grandParent.color = RBColor.RED; // 祖父染成红色
parent.color = RBColor.BLACK; // 父节点染成黑色
root = rightRotate(root, grandParent); // 对祖父右旋
node = root; // 把节点置为根节点退出修复
}
} else { // 父节点为右节点,镜像处理
parentBorther = grandParent.left;
if (parentBorther != RBTreeNode.nullNode && parentBorther.color == RBColor.RED) { // case 1
grandParent.color = RBColor.RED;
parent.color = RBColor.BLACK;
parentBorther.color = RBColor.BLACK;
node = grandParent;
} else {
if (parent.left == node) { // case 2
root = rightRotate(root, parent);
RBTreeNode temp = node;
node = parent;
parent = temp;
}
// case 3
grandParent.color = RBColor.RED;
parent.color = RBColor.BLACK;
root = leftRotate(root, grandParent);
node = root;
}
}
parent = node.p;
}
// 根节点染为黑色
root.color = RBColor.BLACK;
return root;
}
5.删除
讲完插入,我们来讲讲删除操作。与插入类似,再删除前我们先把红黑树当成是一颗普通的二叉搜索树来处理删除节点的操作。但在把节点删除过后,由于删除节点会带走一种颜色,因此我们需要记录下被删除的颜色和删除颜色的位置,最后我们再考虑如何修复树的红黑性质。二叉搜索树删除节点分为三种情况,这里简单提一下:
- 删除节点没有子节点:直接把删除节点的位置置空即可
- 删除节点有一个子节点:用该子节点顶替删除节点的位置
- 删除节点有两个子节点:这是比较复杂的情况,此时我们要从删除节点的两边子树中寻找一个节点来顶替其位置,我们可以找右子树的最小节点或左子树的最大节点,本文给出的代码为寻找右子树的最小节点。同时在代码中我们把删除节点的颜色赋给顶替节点,从而使实际删除颜色的节点为顶替节点。
Java代码如下:
/**
* 红黑树删除操作
* @param root 根节点引用
* @param deleteNode 要删除的节点
* @return 根节点
*/
public static RBTreeNode rbDelete(RBTreeNode root, RBTreeNode deleteNode) {
RBTreeNode replaceNode, fixNode = RBTreeNode.nullNode; // 顶替删除节点的代替节点、需要修复颜色的节点位置
RBTreeNode fixNodeParent = deleteNode.p;
RBColor deleteColor = deleteNode.color; // 记录被删除节点的颜色
if (deleteNode.left == RBTreeNode.nullNode && deleteNode.right == RBTreeNode.nullNode) // 删除节点没有任何子结点
replaceNode = RBTreeNode.nullNode;
else if (deleteNode.right == RBTreeNode.nullNode) { // 处理只有左子节点的情况
replaceNode = deleteNode.left;
fixNode = replaceNode;
} else if (deleteNode.left == RBTreeNode.nullNode) { //处理只有右子节点的情况
replaceNode = deleteNode.right;
fixNode = replaceNode;
} else { // 处理有两个子节点的情况
replaceNode = deleteNode.right;
while (replaceNode.left != RBTreeNode.nullNode) // 找到右子树的最小节点
replaceNode = replaceNode.left;
fixNode = replaceNode.right; // 修复节点位置变为原顶替节点位置
if (replaceNode.p == deleteNode) { // 特殊情况,右子树没有左节点
if (fixNode != RBTreeNode.nullNode) // 修复节点不为空
fixNode.p = replaceNode;
fixNodeParent = replaceNode;
} else {
replaceNode.p.left = fixNode; // 修复节点顶替该节点的位置
if (fixNode != RBTreeNode.nullNode) // 修复节点不为空
fixNode.p = replaceNode.p;
fixNodeParent = replaceNode.p;
replaceNode.right = deleteNode.right;
}
// 用删除节点的颜色代替顶替节点的颜色,使得被删除颜色的节点实际变为顶替节点
deleteColor = replaceNode.color;
replaceNode.color = deleteNode.color;
replaceNode.left = deleteNode.left;
}
if (replaceNode != RBTreeNode.nullNode) // 存在顶替节点
replaceNode.p = deleteNode.p;
if (deleteNode.p == RBTreeNode.nullNode) // 删除节点的父节点为空,是根节点
root = replaceNode;
else { // 删除节点不是根节点
if (deleteNode.p.left == deleteNode)
deleteNode.p.left = replaceNode;
else
deleteNode.p.right = replaceNode;
}
if (deleteColor == RBColor.BLACK) // 如果删除的颜色是黑色则需要进行修复
root = rbDeleteFixup(root, fixNode, fixNodeParent);
return root;
}
首先,如果删除的节点颜色为红色,则不会影响任何红黑性质。但如果删除的颜色是黑色,则可能影响性质2(根节点是黑色的),也可能影响性质4(红色的节点的两个子结点均为黑色),也可能影响性质5(对于每个节点,从该节点到其所有后代的简单路径上,均包含相同数目的黑色节点)。那么当删除的节点颜色为黑色时,对于如何修复删除后的红黑性质,我们采用以下思考方式:
我们假设修复位置的节点具有两种颜色,该节点原来的颜色,以及我们被删除的黑色。那么:
- 如果该节点原来为红色,那么我们被删除的黑色可以直接覆盖其颜色不影响任何红黑性质
- 如果该节点是黑色同时他也是根节点,那么我们可以简单的“消除”掉节点上面的一层黑色
- 如果该节点是黑色,但不是根节点,我们只能通过旋转和重新着色的方法转换修复的位置或退出循环
以下把修复删除红黑性质的工作分为4中情况,此处假设修复位置节点为A(黑色,此处假设为父节点的左节点,右节点请镜像处理),其父节点为B,兄弟节点为C,兄弟节点的左子节点为D,兄弟节点的右子节点为E。
关键词:兄弟节点
情况1:A的兄弟节点为红色
如上图所示,此时我们先交换父节点B和兄弟节点C的颜色,然后对父节点B进行左旋,以上操作并不会影响红黑树性质,而我们也把情况1转化为了别的情况。
情况2:A的兄弟节点为黑色,其子节点均为黑色(下图灰色代表未知颜色)
此时的处理方法很简单,因为A节点和其兄弟节点C均为黑色,且C的子节点也均为黑色,因此我们可以把A节点和C节点的黑色上移到父节点B上,再把修复位置换为父节点B,针对父节点B继续进行修复。(如果父节点B是红色或根节点就可以停止修复了~)
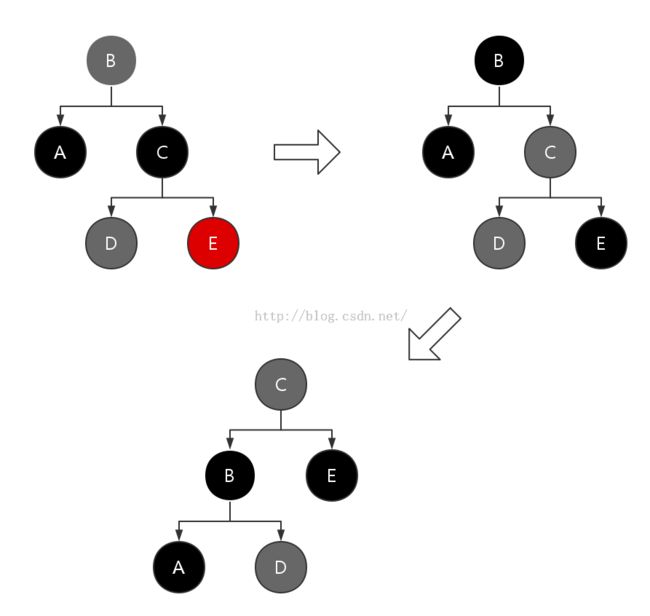
情况3:A的兄弟节点为黑色,兄弟节点的左子节点为红色,右子节点为黑色
此时我们首先交换兄弟节点C与其左子红色节点D的颜色,然后对兄弟节点C进行右旋,把情况3转化为情况4继续处理。
情况4:A的兄弟节点为黑色,兄弟节点的右子节点为红色
此时我们进行如下变换操作:
- 把父节点B和兄弟节点的右子节点E染成黑色,兄弟节点C染成父节点颜色
- 对父节点B进行左旋
以上操作在没有破坏红黑树性质的情况下,消除了节点A的一重黑色,因此至此修复过程可以结束了。
删除时修复过程的Java代码如下:
/**
* 修复删除时破坏的红黑树性质
* @param root 根引用
* @param fixNode 修复位置
* @param parent 修复位置的父节点(修复位置为叶结点时使用)
* @return 根
*/
public static RBTreeNode rbDeleteFixup(RBTreeNode root, RBTreeNode fixNode, RBTreeNode parent) {
RBTreeNode brother;
while (root != fixNode && fixNode.color == RBColor.BLACK) {
parent = fixNode.p == null ? parent : fixNode.p; // 处理fixNode为nullNode情况
if (fixNode == parent.left) { // 顶替位置在父节点左边
brother = parent.right;
if (brother.color == RBColor.RED) { // case 1
// 交换父节点和兄弟节点的颜色
RBColor temp = brother.color;
brother.color = parent.color;
parent.color = temp;
// 父节点进行左旋
root = leftRotate(root, parent);
} else if (brother == RBTreeNode.nullNode) { // case 2
// 兄弟节点为空,即为黑色,只需继续遍历父节点即可
fixNode = parent;
} else if (brother.left.color == RBColor.BLACK &&
brother.right.color == RBColor.BLACK) { // case 2
brother.color = RBColor.RED;
fixNode = parent; // 继续遍历父节点
} else { // case 3 and case 4
if (brother.left.color == RBColor.RED &&
brother.right.color == RBColor.BLACK) { // case 3
// 兄弟节点染成红色,左子节点染成黑色
brother.color = RBColor.RED;
brother.left.color = RBColor.BLACK;
// 兄弟节点右旋
root = rightRotate(root, brother);
brother = brother.p;
}
// case 4
// 变色
brother.color = parent.color;
parent.color = RBColor.BLACK;
brother.right.color = RBColor.BLACK;
// 父节点左旋
root = leftRotate(root, parent);
break;
}
} else {
brother = parent.left;
if (brother.color == RBColor.RED) { // case 1
// 交换父节点和兄弟节点的颜色
RBColor temp = brother.color;
brother.color = parent.color;
parent.color = temp;
// 父节点进行右旋
root = rightRotate(root, parent);
} else if (brother == RBTreeNode.nullNode) { // case 2
// 兄弟节点为空,即为黑色,只需继续遍历父节点即可
fixNode = parent;
} else if (brother.left.color == RBColor.BLACK &&
brother.right.color == RBColor.BLACK) { // case 2
brother.color = RBColor.RED;
fixNode = parent; // 继续遍历父节点
} else { // case 3 and case 4
if (brother.right.color == RBColor.RED &&
brother.left.color == RBColor.BLACK) { // case 3
// 兄弟节点染成红色,左子节点染成黑色
brother.color = RBColor.RED;
brother.right.color = RBColor.BLACK;
// 兄弟节点右旋
root = leftRotate(root, brother);
brother = brother.p;
}
// case 4
// 变色
brother.color = parent.color;
parent.color = RBColor.BLACK;
brother.left.color = RBColor.BLACK;
// 父节点左旋
root = rightRotate(root, parent);
break;
}
}
}
fixNode.color = RBColor.BLACK;
return root;
};
6.打印与测试函数
这里给出本人用来测试和打印红黑树的Java函数:
public static void main(String[] args) {
int num[] = new int[]{5, 4, 1, 6, 3, 2};
List<RBTreeNode> list = new ArrayList<>();
RBTreeNode root = RBTreeNode.nullNode;
// 插入测试
for (int i = 0; i < num.length; i++) {
list.add(new RBTreeNode(num[i]));
root = rbInsert(root, list.get(i));
printRBTree(root);
System.out.println("");
}
// 删除测试
for (int i = 0; i < num.length; i++) {
root = rbDelete(root, list.get(0));
list.remove(0);
printRBTree(root);
System.out.println("");
}
}
/**
* 打印一颗红黑树
* @param root 根节点的引用
*/
public static void printRBTree(RBTreeNode root) {
if (root == RBTreeNode.nullNode) {
System.out.println("这是一颗空树");
return;
}
Queue<RBTreeNode> q = new LinkedList<>();
boolean allNull = false; // 是否全为空节点
q.add(root);
while (!allNull) { // 该行不是全为叶结点
allNull = true;
Queue<RBTreeNode> rowQ = new LinkedList<>(); // 用于存储一行的所有节点
RBTreeNode node;
while (!q.isEmpty()) {
node = q.poll();
System.out.print(node);
if (node != RBTreeNode.nullNode) { // 该节点不是叶结点
if (node.left != RBTreeNode.nullNode) {
rowQ.add(node.left);
allNull = false;
} else
rowQ.add(RBTreeNode.nullNode);
if (node.right != RBTreeNode.nullNode) {
rowQ.add(node.right);
allNull = false;
} else
rowQ.add(RBTreeNode.nullNode);
} else { // 该节点为叶节点
rowQ.add(RBTreeNode.nullNode);
rowQ.add(RBTreeNode.nullNode);
}
}
q = rowQ;
System.out.println("");
}
}
总结,没写不知道,一写吓一跳,用Java来实现红黑树还是有挺多麻烦点的:
- 在Java中不知道如何修改根引用,所以最后都在函数上补了返回值
- 刚开始没考虑null叶节点其实是算黑色节点的情况,后来补充了一个静态变量作为叶节点
- 用静态变量当叶节点使得叶节点是共享的,不能修改叶节点的left,right,p指针,因此又再删除时添加了fixParent变量
- 删除时拥有两个子树,但右子树没有左节点的情况是个坑……
总而言之,红黑树的5个性质,3种插入情况,4种删除情况记住就大概没什么问题了~