程序设计竞赛常用技巧精选
对《挑战程序设计竞赛》的一个记录
第三章 出类拔萃——中级篇
3.2 常用技巧精选
(1)尺取法
poj 3061 Subsequence
给定长度为n的数列整数a0,a1,…an-1以及证书S。求出总和不小于S的连续子序列的长度的最小值。如果解不存在在,则输出0.
已知:
10 < n < 10^5
0 < ai ≤ 10^4
S < 10^8
sample input
n = 10
S = 15
a = {5,1,3,5,10,7,4,9,2,8}
sample output
2 (5 + 10)
这题比较好想的一个思路就是先求出前n项的和,再在满足sum>=S的时候,val = sum - S,二分查找之前的项中满足≤val的最大项。
例如:
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| a : | 5 | 1 | 3 | 5 | 10 | 7 | 4 | 9 | 2 | 8 |
| sum: | 5 | 6 | 9 | 14 | 24 | 31 | 35 | 44 | 46 | 54 |
第一个满足sum >= 15的值是下标为4的值,以此为例,前5项的和为24,val = 24 - 15 = 9,我要找前5项中sum<=9的最大小标,可以找到是小标为2的值,因此可得到连续子序列最小的长度为4 - 2 = 2 即5 + 10
这个算法的时间复杂度为:O( nlogn )
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 100010;
int T,n,s;
int sum[Maxn];
int solved(int l,int r,int k)
{
while(l <= r)
{
int mid = (l + r) / 2;
if(sum[mid] <= k)
l = mid + 1;
else
r = mid - 1;
}
return r;
}
int main()
{
int a;
sf("%d",&T);
while(T--)
{
sf("%d%d",&n,&s);
for(int i = 0;i < n;i ++)
{
sf("%d",&a);
if(i == 0) sum[i] = a;
else sum[i] = sum[i - 1] + a;
}
int Min = n + 1;
for(int i = 0;i < n;i ++)
{
if(sum[i] >= s)
Min = min(Min,i - solved(0,i,sum[i] - s));
}
pf("%d\n",Min > n?0:Min);
}
return 0;
}
那什么是尺取法?尺取法能更高效地解决此类问题。
我们设以 as 开始总和最初大于S时的连续子序列 as+...+at−1 ,这时
as+1+...+at−2<as+...+at−2<S
所以从 as+1 开始总和最初超过S的连续子序列如果是 as+1+...+at′−1 的话,则必然有 t≤t′ 。
用下面的图来解释比较清晰:
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 100010;
int T,n,s;
int sum[Maxn];
int main()
{
int a;
sf("%d",&T);
while(T--)
{
int tail = -1,head = -1;
sf("%d%d",&n,&s);
for(int i = 0;i < n;i ++)
{
sf("%d",&a);
if(i == 0) sum[i] = a;
else sum[i] = sum[i - 1] + a;
if(tail == -1 and sum[i] >= s)
tail = i;
}
if(tail == -1)
{
pf("0\n");
continue;
}
int Min = n;
while(head < tail)
{
if(sum[tail] - sum[head + 1] >= s)
{
head ++;
Min = min(Min,tail - head);
}
else if(tail < n - 1) tail++;
else
break;
}
pf("%d\n",Min);
}
return 0;
}
尺取法的算法复杂度为O(n)
两个程序结果比较如下:(第一行为尺取法,第二行为二分的方法)
![]()
poj 3320 Jessica’s Reading Problem
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 1000010;
map<int,int> mp,tmp;
int p[Maxn];
int n;
int main()
{
while(~sf("%d",&n))
{
mp.clear();
tmp.clear();
for(int i = 0;i < n;i ++)
{
sf("%d",&p[i]);
mp[p[i]]++;
tmp[p[i]]++;
}
int s = mp.size();
int tail = 0, head = 0;
int num = 1,Min = n;
tmp[p[0]]--;
while(head <= tail)
{
if(num < s && tail < n - 1)
{
tail ++;
if(tmp[p[tail]] == mp[p[tail]])
num ++;
tmp[p[tail]] --;
}
else if (num == s)
{
Min = min(Min,tail - head + 1);
tmp[p[head]] ++;
if(tmp[p[head]] == mp[p[head]])
num --;
head ++;
}
else
break;
}
pf("%d\n",Min);
}
return 0;
}
(2) 反转(开关问题)
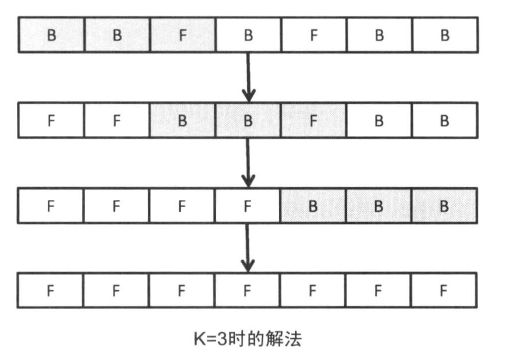
POJ 3276 Face The Right Way
N头牛排列成了一列,每头牛或者向前或者向后站,为了让所有的牛都面向前方,农夫约翰买了一台自动转向的机器,这个机器在购买时就必须设定一个数值K,机器每操作一次恰好使K头连续的牛转向(K头牛分别为当前的牛及其之后的牛,不影响位于它之前的牛,并且每次反转必须是K头牛,不可以少于K头)。请求出为了让所有的牛都能面向前方需要的最少的操作次数M和对应的最小的K。
已知:
1 ≤ N ≤ 5000
sample input
N = 7
BBFBFBB(F:面向前方,B:面向后方)
sample output
K = 3
M = 3
(先反转1~3号的三头牛,然后再反转3~5号,最后反转5~7号)
这题还算比较好做,主要有个条件是从当前牛开始,与位于其后的共K头牛进行反转。判断第i头牛是否需要反转,只需要根据能影响到它的第 i - K+1,…,i - 1头牛的反转情况就可以确定了。
令
f[i]:=区间[i,i + K - 1]进行了反转的话则为1,否则为0。
sum = f[i - k + 1] + f[i - k + 2] + …+f[i - 1];
如果sum为奇数,表明第i头牛被反转了,如果原来的牛是面向后方的(B),则被转成面向前方了,f[i] = 0,不用继续反转了;如果原来的牛是面向前方的(F),则被转成了面向后方,需要再次反转过来,f[i] = 1。
在计算过程中,我们只要一个值来记录当前牛之前的K-1头牛的f[j]之和,就可以算出当前牛的f[i]
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 5010;
int f[Maxn],n;//f[i],以i开头,长度为k的区间是否需要反转,需要f为1,否则为0
char s[Maxn];
void solved()
{
int num = n,len = 1;
for(int k = 1;k <= n;k ++)
{
int flag = 0,cnt = 0,sum =0;
for(int i = 0;i < n;i ++)
{
if(i >= k) sum -= f[i - k];//记录当前位置前k-1个值总共
if(sum & 1)
f[i] = (s[i] == 'F')?1:0;
else
f[i] = (s[i] == 'F')?0:1;
sum += f[i];
if(f[i] == 1)
{
if(i + k > n)//反转区间长度<k,则不符合条件
{
flag = 1;
break;
}
cnt ++;//反转区间个数统计
}
}
if(flag == 0)
{
if(cnt < num)
num = cnt,len = k;
}
}
pf("%d %d\n",len,num);
}
int main()
{
while(~sf("%d",&n))
{
for(int i = 0;i < n;i ++)
getchar(),sf("%c",&s[i]);
solved();
}
return 0;
}
POJ 3279 Fliptile
农夫约翰知道聪明的牛产奶多。于是为了提高牛的智商他准备了如下游戏。有一个M×N 的格子,每个格子可以翻转正反面,它们一面是黑色,另一面是白色。黑色的格子翻转后就是白色,白色的格子翻转过来则是黑色。游戏要做的就是把所有的格子都翻转成白色。不过因为牛蹄很大,所以每次翻转一个格子时,与它上下左右相邻接的格子也会被翻转。因为翻格子太麻烦了,所以牛都想通过尽可能少的次数把所有格子都翻成白色。现在给定了每个格子的颜色,请求出用最小步数完成时每个格子翻转的次数。最小步数的解有多个时,输出字典序最小的一组。解不存在的话,则输出IMPOSSIBLE。
已知:
1 ≤ M,N ≤ 15
sample input
M = 4
N = 4 每个格子的颜色如下:(0表示白色,1表示黑色)
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
sample output
0 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0
如果继续按照上面那题的思路,会发现行不通,因为(1,1)反转时会同时反转(1,2)和(2,1),但是当(1,2)反转时(1,1)又会受到影响,再次反转。
于是不妨先指定好最上面一行的反转方法,此时能够反转(1,1)的只剩下(2,1)了,所以可以直接判断(2,1)是否需要反转,类似的(2,1)~(2,N)都能这样判断,如此反复,如果最后一行并非全白色,则意味着不存在可行的操作方法。
这样算法的复杂度为O(MN 2N ) ,先对第一排进行0~(1 << N )- 1的数值枚举,1代表反转,0代表不反转,然后依次根据上一行的数据判断当前行有哪些需要反转。
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 20;
int n,m;
int a[Maxn][Maxn],b[Maxn][Maxn],ans[Maxn][Maxn],tmp[Maxn][Maxn];
int Find[20] = {0,1,0,-1,0,1,0,-1,0,0};
void solved()
{
int len = (1 << m) - 1;
int flag = 0,Min = n * m + 1;
for(int k = 0;k <= len;k ++)//枚举第一行的反转情况
{
memcpy(b,a,sizeof(a));
int val = k,step = 0;
for(int j = 0;j < m;j ++)
{
if(val & 1)
{
for(int z = 0;z < 5;z ++)
{
if(Find[z] <0 || Find[z] >=n || j + Find[z + 5] < 0 || j + Find[z + 5] >= m) continue;
b[Find[z]][j + Find[z + 5]] ^= 1;
}
step ++;
}
tmp[0][j] = val & 1;
val >>= 1;
}
for(int i = 1;i < n;i ++)//第二行开始,根据前一行的信息判断当前点是否需要反转
for(int j = 0;j < m;j ++)
{
if(b[i - 1][j] == 1)
{
for(int z = 0;z < 5;z ++)//一个点反转同时影响周围4个点。
{
if(i + Find[z] <0 || i + Find[z] >=n || j + Find[z + 5] < 0 || j + Find[z + 5] >= m) continue;
b[i + Find[z]][j + Find[z + 5]] ^= 1;
}
tmp[i][j] = 1;
step ++;
}
else
tmp[i][j] = 0;
}
int sum = 0;
for(int j = 0;j < m;j ++)
sum += b[n - 1][j];
if(sum == 0)
{
if(step < Min)//寻找步数小的解
{
memcpy(ans,tmp,sizeof(tmp));
Min = step;
}
flag = 1;
}
}
if(flag == 0)
pf("IMPOSSIBLE\n");
else
{
for(int i = 0;i < n;i ++)
{
for(int j = 0;j < m - 1;j ++)
pf("%d ",ans[i][j]);
pf("%d\n",ans[i][m - 1]);
}
}
}
int main()
{
while(~sf("%d%d",&n,&m))
{
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
sf("%d",&a[i][j]);
solved();
}
return 0;
}
ps:poj上的这个题数据可能有点问题,题目虽然说了如果存在多个解就按输出字典序最小的那个,但是只要在枚举过程中找到一个就输出然后return也是可以的,并不涉及多个解的情况,不知道是不是因为从0开始枚举,遇到的第一个答案就是步数最少的解,没验证过。。。
这题的另外一个做法是高斯消元(高斯消元可以查看之前的一篇文章)
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 20;
int a[Maxn][Maxn];
int paint[Maxn * Maxn][Maxn * Maxn],ans[Maxn * Maxn];
int Find[20] = {0,1,0,-1,0,1,0,-1,0,0};
void Guass(int n,int m)
{
int i,row,col;
for(row = 0,col = 0; row < n && col < n; row ++,col ++)
{
for(i = row;i < n;i ++)
if(paint[i][col] == 1) break;
if(i == n)
{
row --;
continue;
}
if(i != row)
{
for(int j = 0;j < n + 1;j ++)
swap(paint[row][j],paint[i][j]);
}
for(i = row + 1;i < n;i ++)
if(paint[i][col])
{
for(int j = col;j < n + 1;j ++)
paint[i][j] ^= paint[row][j];
}
}
for(i = row;i < n;i ++)
if(paint[i][n] != 0)
{
pf("IMPOSSIBLE\n");
return;
}
int num = 1 << (n - row),cnt = 0,Min = n + 1;
for(i = 0;i < num;i ++)
{
cnt = 0;
for(int j = n - 1,pos = i;j >= row;j--,pos >>= 1)
{
paint[j][j] = pos & 1;
if(paint[j][j]) cnt ++;
}
for(int j = row - 1;j >= 0;j --)
{
int tmp = 0;
for(int k = j + 1;k < n;k ++)
{
if(paint[j][k] == 0) continue;
tmp ^= paint[k][k];
}
paint[j][j] = paint[j][n]^tmp;
if(paint[j][j]) cnt ++;
}
if(cnt < Min)
{
Min = cnt;
for(int j = 0;j < n;j ++)
ans[j] = paint[j][j];
}
}
for(int i = 0;i < n;i ++)
{
if(i % m == 0)
pf("%d",ans[i]);
else
pf(" %d",ans[i]);
if((i + 1) % m == 0)
pf("\n");
}
}
int main()
{
int n,m;
while(~sf("%d%d",&n,&m))
{
memset(paint,0,sizeof(paint));
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
{
sf("%d",&a[i][j]);
for(int k = 0;k < 5;k ++)
{
int x = i + Find[k];
int y = j + Find[k + 5];
if(x < 0 || x >= n || y < 0 || y >= m) continue;
paint[i * m + j][x * m + y] = 1;
}
paint[i * m + j][n * m] = a[i][j];
}
Guass(n * m,m);
}
return 0;
}
/* 3 3 0 1 0 1 0 1 0 1 0 */(3) 弹性碰撞
POJ 3684 Physics Experiment
用N个半径为R厘米的球进行如下实验。
在H米高的位置设置一个圆筒,将求垂直放入(从下向上数第i个球的底端距离地面高度为H + 2R)。实验开始时最下面的球开始掉落,此后每一秒又有一个球开始掉落。不计空气阻力,并假设球与球或地面间的碰撞时弹性碰撞。
请求出实验开始后T秒时每个球底端的高度。假设重力加速度为 g=10m/s2
已知:
1 ≤ N ≤ 100
1 ≤ H ≤ 10000
1 ≤ R ≤ 100
1 ≤ T ≤ 10000
sample input
N = 1
H = 10
R = 10
T = 100
sample output
4.95
看到这题我就想到了Ants这道题
从高位H的位置下落的话需要花费的时间:
H=12gt2
所以, t=2Hg−−−√
因此,在时刻T时,令K 为满足kt ≤ T的最大整数,那么
当R = 0时,如果认为球是一样的,就可以忽视他们的碰撞,视为直接互相穿过继续运动。由于在有碰撞时球的顺序不会发生改变,所以忽略碰撞,将计算得到的坐标进行排序后,就能知道每个球的最终位置。
那么,R>0是要怎么样?这种情况下的处理方法基本相同,对于下方开始的第i个球,在按照R = 0计算的结果上加上2*R*i就可以了
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
#define sf scanf
#define pf printf
using namespace std;
const int Maxn = 110;
double ans[Maxn];
int main()
{
int cas,N,H,R,T,g = 10;
sf("%d",&cas);
while(cas--)
{
sf("%d%d%d%d",&N,&H,&R,&T);
for(int i = 0;i < N;i ++)
{
double t = sqrt(2.0 * H / g);
int k = floor(T / t);
if(k < 0)
ans[i] = H;
else
{
if(k & 1)
ans[i] = H - 0.5 * g * (t - (T - k * t)) * (t - (T - k * t));
else
ans[i] = H - 0.5 * g * (T - k * t) * (T - k * t);
}
T --;
}
sort(ans,ans + N);
for(int i = 0;i < N;i ++)
pf("%.2lf%c",ans[i] + 2.0 * R * i / 100,i + 1 == N ? '\n':' ');
}
return 0;
}
/* 2 1 10 10 100 2 10 10 100 */
(4)折半枚举(双向搜索)
POJ 2785 4 Values whose Sum is 0
给定各有n个整数的四个数列A,B,C,D。要从每个数列中各取出1个数,使得四个数的和为0,这出这样的组合的个数。当一个数列中有多个相同的数字时,把它们作为不同的数字看待。
已知:
1 ≤ n ≤ 4000
|(数字的值)| ≤228
sample input
n = 6
A = {-45,-41,-36,-36,26,-32}
B = {22,-27,53,30,-38,-54}
C = {42,56,-37,-75,-10,-6}
D = {-16,30,77,-46,62,45}
sample output
5
如果全部枚举,则有 n4 种可能性。时间复杂度通不过。因此可以进行折半枚举,计算A,B之间的组合,共有 n2 种情况,同样的,C,D之间也有 n2 种情况。
在取出A,B组合中的一组组合(a + b)时,为了使和为0,去查找C,D组合中满足a + b+c+d = 0的组合(c+d),这个查找可以用二分查找来实现,因此最后的复杂度是O( n2logn )
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
#define sf scanf
#define pf printf
using namespace std;
typedef long long LL;
const int Maxn = 4010;
int A[Maxn],B[Maxn],C[Maxn],D[Maxn];
int AB[Maxn * Maxn],CD[Maxn * Maxn];
int n;
LL solved(int val)
{
int l = 0, r = n * n - 1;
LL ans;
while(l <= r)
{
int mid = (l + r) / 2;
if(CD[mid] <= val)
l = mid + 1;
else
r = mid - 1;
}
ans = r;
l = 0, r = n * n - 1;
while(l <= r)
{
int mid = (l + r) / 2;
if(CD[mid] < val)
l = mid + 1;
else
r = mid - 1;
}
ans = ans - r;
return ans;
}
int main()
{
while(~sf("%d",&n))
{
for(int i = 0;i < n;i++)
sf("%d%d%d%d",&A[i],&B[i],&C[i],&D[i]);
int cnt = 0;
for(int i = 0;i < n;i ++)
for(int j = 0;j < n;j ++)
AB[cnt] = A[i] + B[j],CD[cnt++] = C[i] + D[j];
sort(CD,CD + cnt);
LL ans = 0;
for(int i = 0;i < cnt;i ++)
ans += solved(0 - AB[i]);
pf("%lld\n",ans);
}
return 0;
}
/* 3 0 0 0 0 0 0 0 0 0 0 0 0 */
超大背包问题:
有重量和价值分别为 wi,vi 的n个物品。从这些物品中挑选总重量不超过W的物品,求所有挑选方案中价值总和的最大值。
已知:
1 ≤ n ≤ 40
1 ≤wi,vi≤1015
1 ≤W≤1015
sample input
n = 4
w = {2 , 1 , 3 , 2}
v = {3 , 2 , 4 , 2}
W = 5
sample output
7(挑选0,1,3号物品)
如果这个题用背包问题来做,W太大,内存不够,但是这题中n的范围很小。因此可以用枚举来做。
挑选物品的方法共有 2n 种,所以不能直接枚举,可以考虑使用折半枚举, 220 是可以接受的。前半部分选取对应的重量和价值总和记为w1,v1。这样在后半部分寻找总重 w2≤W−w1 时使v2最大的选取方法就好了。
因此,主要思考从枚举得到的(w2,v2)的集合中高效寻找 max{v2|w2≤W′} 的方法。首先排除 w2[i]≤w2[j] 且 v2[i]≥v2[j] 中的j, 此后剩余的元素都满足w2[i] < w2[j] , v2[i] < v2[j] ,可使用二分搜索进行查找。算法总复杂度为O( 2(n/2)n )。
(5) 坐标离散化
区域的个数
w*h的格子上画了n条或垂直或水平的宽度为1的直线,求出这些线将格子划分成了多少个区域。
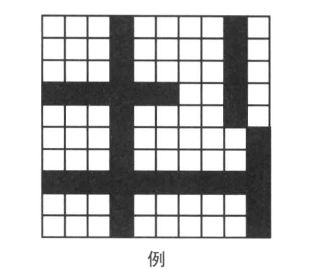
已知:
1≤w,h≤1000000
1≤n≤500
sample input
w = 10,h = 10,n = 5
x1 = {1 , 1 , 4 , 9 , 10}
y1 = {4 , 8 , 1 , 1 , 6}
x2 = {6 , 10 , 4 , 9 , 10}
y2 = {4 , 8 , 10 , 5 , 10}
(对应上图,横向为x,纵向为y)
利用BFS或dfs可以求出被分割的区域,但是w,h太大,不能创建w*h的数组,所以需要用到“坐标离散化” 这一技巧。
如下图:

将前后左右没有变化的行列消除后并不会影响区域的个数。数组里重要存储有直线的行列以及其前后的行列就足够了。这样的话最多6n*6n就足够了,因此可以创建出数组并利用搜索求出区域的个数。