树状数组-HDU1166

题意为：

T组测试数组，

跟着一个整数n,n(n<=50000),表示N个营地

n后面跟着n个数ai(1~50).，表示每个营地人数。

然后输入三种操作（最多有40000条操作）;

1.Add x y ：x营地增加y人。

2.Query x y：查询x~y营地的总人数。
3.Sub x y : x营地减少y人。
End：结束。

如果按常规方法一个一个查询人数，时间复杂度为O（n*m）,即2*10^9,超时。

下面看看树状数组：

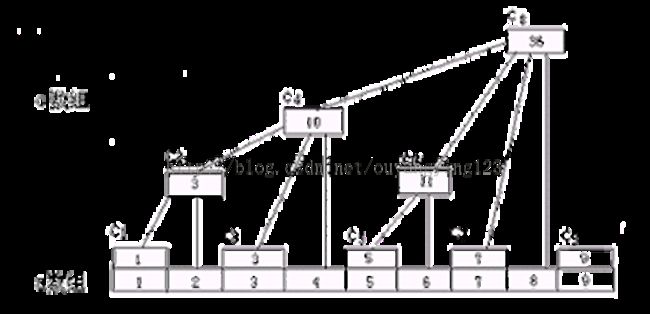
a数组储存营地人数，现在我们定义一个索引数组c[],储存方式如图所示。

定义一个函数fsum（），通过索引数组求前N项和。fsum()按二进制求和;

比如：fsum(5)=c[5]+c[4]   fsum(7)=c[7]+c[6]+c[4].

               101  100                 111   110  100  .

每次加上x转为二进制，去掉最后一位1得到的数。

 代码如下：

#include <stdio.h>
#include <string.h>
#include <iostream>
#define MAX 50005

int c[MAX];

inline int lowbit(int x)                  //inline为内联函数，节省时间
{
    return x&(-x);                                  //lowbit()函数返回x二进制最左边的1以及左边的0。
}                       <span style="font-family: Arial, Helvetica, sans-serif;">  </span><span style="font-family: Arial, Helvetica, sans-serif;">//  比如 x=6=1 1 0   lowbit(x)= 1 0 =2.</span>

int fsum(int x)               <span style="font-family: Arial, Helvetica, sans-serif;">//通过索引数组C求前X的和。</span>
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
void add(int x,int v,int n)                      //新增一个数v，更新索引数组C[]
{
    while(x<=n)
    {
        c[x]+=v;
        x=x+lowbit(x);
    }
}

int main()
{
    int t;
    scanf("%d",&t);
    for(int j=1;j<=t;j++)
    {
        memset(c,0,sizeof(c));
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            add(i,x,n);
        }
        printf("Case %d:\n",j);
        char s[20];
        while(scanf("%s",s) && s[0]!='E')
        {
            int x,y;
            scanf("%d %d",&x,&y);
            if(s[0]=='A')
                add(x,y,n);
            else if(s[0]=='S')
                add(x,-y,n);
            else if(s[0]=='Q')
                printf("%d\n",fsum(y)-fsum(x-1));
        }
    }
    return 0;
}

树状数组的难点在于理解索引数组C[]的储存方式，以及通过索引数组求前X项的和。