立方体Z-Buffer消隐算法
Z-Buffer消隐算法<计算机图形学实践教程VC++ 孔令德>:
主要函数:
void ReadPoint();//读入顶点表函数,此处为立方体的8个顶点m_point[8]
void ReadColor();//读入颜色函数,即立方体六个面的颜色
void ReadFace();//读入面表函数,即设置面上4个点的索引值
void PolygonFill(CDC*);//填充多边形函数
void CreatBucket();//建立桶结点函数
void Et();//构造边表函数
void AddAet(Edge *);//将边插入Aet表函数
void AetOrder();//对Aet表进行排序函数
bool m_Paint(CDC*);//着色函数
void Angle();//旋转角度函数
void Sign(CDC* mdc);//输出图标函数
void ZBuffer();//
函数调用关系图如下:
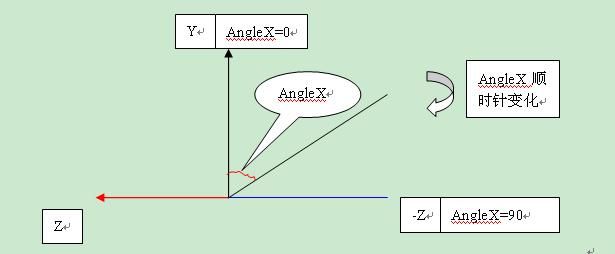
下图是Angle()中角度变化时点的旋转,坐标系是从opengl的X轴正向看过去时的情况,即物体绕X轴旋转AngleX度,该角度是以Y轴正向为基准的,且顺时针方向为正.当Angle=0时,就是Y轴正向;当Angle=90时,变为-Z轴.
代码如下:
void CTestView::ZBuffer()/调用m_Paint函数
{
CRect Rect;
GetClientRect(&Rect);
CClientDC dc(this);
dc.SetMapMode(MM_ANISOTROPIC);//自定义坐标系
dc.SetWindowExt(Rect.Width(),Rect.Height());
dc.SetViewportExt(Rect.right,-Rect.bottom);//x轴垂直向右,y轴垂直向上
dc.SetViewportOrg(Rect.right/2,Rect.bottom/2);//屏幕中心为圆心
CDC MemDC;
MemDC.CreateCompatibleDC(GetDC());
MemDC.SetMapMode(MM_ANISOTROPIC);
MemDC.SetWindowExt(Rect.Width(),Rect.Height());
MemDC.SetViewportExt(Rect.right,-Rect.bottom);
MemDC.SetViewportOrg(Rect.right/2,Rect.bottom/2);
CBitmap Bitmap,*OldBitmap;
Bitmap.LoadBitmap(IDB_BITMAP2);
OldBitmap=MemDC.SelectObject(&Bitmap);
MemDC.BitBlt(-Rect.right/2,-Rect.bottom/2,Rect.Width(),Rect.Height(),&Picture,-Rect.right/2,-Rect.bottom/2,SRCCOPY);
m_Paint(&MemDC);
dc.BitBlt(-Rect.right/2,-Rect.bottom/2,Rect.right,Rect.bottom,&MemDC,-Rect.right/2,-Rect.bottom/2,SRCCOPY);
MemDC.SelectObject(OldBitmap);
}
void CTestView::OnMenuReset()//菜单函数
{
// TODO: Add your command handler code here
m_AngleX=m_AngleY=0;
Angle();
RedrawWindow();
MessageBox("使用方向键旋转立方体!","信息",MB_ICONINFORMATION|MB_OK);
}
void CTestView::ReadPoint()//读入顶点表函数,此处为立方体的8个顶点m_point[8]
{
//设置多边形的8个顶点
m_OldBox.m_Point[0].x=-100;m_OldBox.m_Point[0].y=-100;m_OldBox.m_Point[0].z=+100;
m_OldBox.m_Point[1].x=+100;m_OldBox.m_Point[1].y=-100;m_OldBox.m_Point[1].z=+100;
m_OldBox.m_Point[2].x=+100;m_OldBox.m_Point[2].y=-100;m_OldBox.m_Point[2].z=-100;
m_OldBox.m_Point[3].x=-100;m_OldBox.m_Point[3].y=-100;m_OldBox.m_Point[3].z=-100;
m_OldBox.m_Point[4].x=-100;m_OldBox.m_Point[4].y=+100;m_OldBox.m_Point[4].z=+100;
m_OldBox.m_Point[5].x=+100;m_OldBox.m_Point[5].y=+100;m_OldBox.m_Point[5].z=+100;
m_OldBox.m_Point[6].x=+100;m_OldBox.m_Point[6].y=+100;m_OldBox.m_Point[6].z=-100;
m_OldBox.m_Point[7].x=-100;m_OldBox.m_Point[7].y=+100;m_OldBox.m_Point[7].z=-100;
}
void CTestView::ReadFace()//读入面表函数,即设置每个面上4个点的索引值
{
F[0][0]=4;F[0][1]=0;F[0][2]=1;F[0][3]=2;F[0][4]=3;
F[1][0]=4;F[1][1]=0;F[1][2]=3;F[1][3]=7;F[1][4]=4;
F[2][0]=4;F[2][1]=0;F[2][2]=1;F[2][3]=5;F[2][4]=4;
F[3][0]=4;F[3][1]=1;F[3][2]=2;F[3][3]=6;F[3][4]=5;
F[4][0]=4;F[4][1]=4;F[4][2]=5;F[4][3]=6;F[4][4]=7;
F[5][0]=4;F[5][1]=3;F[5][2]=2;F[5][3]=6;F[5][4]=7;
}
void CTestView::ReadColor()//读入颜色函数, 即立方体六个面的颜色
{
RGB[0]=RGB(255,255,0);
RGB[1]=RGB(0,255,255);
RGB[2]=RGB(0,0,255);
RGB[3]=RGB(0,255,0);
RGB[4]=RGB(255,0,0);
RGB[5]=RGB(255,0,255);
}
bool CTestView::m_Paint(CDC* mdc)//着色函数,用一个循环对六个面进行填充,每次都对深度进行比较,深度大的(即离视点近的)会保持在前面.画一个平面时用有效边表填充算法(用到了桶和有效边表).
{
Sign(mdc);
Angle();
for(int i=0;i<=400;i++)
for(int j=0;j<=400;j++)
ZB[i][j]=-500;
for(Face=0;Face<6;Face++)
{
int TotalEdge=F[Face][0];
for(int edge=1;edge<=TotalEdge;edge++)//边循环
{
int PointNumber=F[Face][edge];//面的顶点号;
Point[edge-1]=m_Box.m_Point[PointNumber];
}
CreatBucket();//建立桶结点
Et();//用于建立边表
PolygonFill(mdc);//进行填充
}
return true;
}
void CTestView::Angle()//旋转角度函数,此处计算将立方体的8个顶点分别绕X轴,Y轴旋转后的新点的坐标,是世界坐标值,这与<计算机图形学实践教程VC++ 孔令德>里的改变坐标系是相反的一个过程,即点与坐标系相对运动:如想把点绕Y轴转动A度,则相当于把坐标系绕Y轴转动-A度.此函数中,绕X轴旋转,相当于一个圆锥,x不变, (y,z)在一个圆上转了一个角度,可直接求出新的(y’,z’).从下面TmpPoint值可以看出,当AngleX=0时,新点坐标为(x,y,z),即为Y轴正向;当AngleX=90时, 新点坐标为(x,z,-y),即为-Z轴正向(可取x=0,y=1,z=0看).从X轴正向观看,当旋转角度为正时,物体顺时针转动.故想看物体上面部分时,可按向上键,此时角度减10度,即逆时针旋转,相当于把物体上面的点下移,也就看到了上面的点.如前面图所示.
{//将Boxx方向旋转m_AngleX度,y方向旋转m_AngleY度
for(int i=0;i<8;i++)//Box有8个顶点
{
MyPoint TmpPoint;
TmpPoint.x=m_OldBox.m_Point[i].x;
TmpPoint.y=ROUND(m_OldBox.m_Point[i].y*cos(m_AngleX*PI/180)+m_OldBox.m_Point[i].z*sin(m_AngleX*PI/180));
TmpPoint.z=ROUND(-m_OldBox.m_Point[i].y*sin(m_AngleX*PI/180)+m_OldBox.m_Point[i].z*cos(m_AngleX*PI/180));
m_Box.m_Point[i].x=ROUND(-TmpPoint.z*sin(m_AngleY*PI/180)+TmpPoint.x*cos(m_AngleY*PI/180));
m_Box.m_Point[i].y=TmpPoint.y;
m_Box.m_Point[i].z=TmpPoint.z*cos(m_AngleY*PI/180)+TmpPoint.x*sin(m_AngleY*PI/180);
}
}
void CTestView::OnKeyDown(UINT nChar, UINT nRepCnt, UINT nFlags)//键盘控制函数
{
switch(nChar)
{
case VK_UP:
m_AngleX+=10;
break;
case VK_DOWN:
m_AngleX-=10;
break;
case VK_LEFT:
m_AngleY+=10;
break;
case VK_RIGHT:
m_AngleY-=10;
break;
default:
break;
}
if (m_AngleX>=360)//角度不能大于360,也不能小于0
{
m_AngleX-=360;
}
else if (m_AngleX<0)
{
m_AngleX=360+m_AngleX;
}
if (m_AngleY>=360)
{
m_AngleY-=360;
}
else if (m_AngleY<0)
{
m_AngleY=360+m_AngleY;
}
ZBuffer();
CView::OnKeyDown(nChar,nRepCnt,nFlags);
}
void CTestView::Sign(CDC* mdc) //输出图标
{
CPoint p1[4];
CString c[7];
c[0]="底面:";
c[1]="左面:";
c[2]="前面:";
c[3]="右面:";
c[4]="顶面:";
c[5]="后面:";
c[6]="博创研究所版权所有";
mdc->SetBkColor(RGB(0,0,0));
mdc->SetTextColor(RGB(255,255,255));
mdc->TextOut(-500,300,c[6]);
CBrush MyBrush,*OldBrush;
for(int i=0;i<6;i++)
{
MyBrush.CreateSolidBrush(RGB[i]);
OldBrush=mdc->SelectObject(&MyBrush);
mdc->TextOut(-500,280-i*20,c[i]);
p1[0].x=-450;p1[0].y=280-i*20;
p1[1].x=-430;p1[1].y=280-i*20;
p1[2].x=-430;p1[2].y=265-i*20;
p1[3].x=-450;p1[3].y=265-i*20;
mdc->Polygon(p1,4);
mdc->SelectObject(OldBrush);
MyBrush.DeleteObject();
}
}
void CTestView::PolygonFill(CDC* mdc)//多边形填充
{
//计算直线deep增量
double CurDeep=0.0;//当前扫描线的深度
double DeepStep=0.0;//当前扫描线随着x增长的深度步长
double A=0.0;//平面方程系数A
double B=0.0;//平面方程系数B
double C=0.0;//平面方程系数C
double D=0.0;//平面方程系数D
//计算当前面方程Ax+By+Cz+D=0的系数,(A,B,C)即为平面的法向量.设平面三个点为M,N,P,则法向量为AB*AC(叉乘).
A=(Point[1].y-Point[2].y)*(Point[1].z-Point[3].z)-(Point[1].y-Point[3].y)*(Point[1].z-Point[2].z);
B=(Point[1].x-Point[3].x)*(Point[1].z-Point[2].z)-(Point[1].z-Point[3].z)*(Point[1].x-Point[2].x);
C=(Point[1].x-Point[2].x)*(Point[1].y-Point[3].y)-(Point[1].x-Point[3].x)*(Point[1].y-Point[2].y);
D=-A*Point[1].x-B*Point[1].y-C*Point[1].z;
//计算curDeep;从x=xMin开始计算,此时针对yi,相当于yi不变,而求X,Z平面上线的斜率一样,这样每次当X增加1时,Z也会相应地加上此斜率值,这样才能保证点依然在该直线(是三维的直线)上.
DeepStep=-A/C;
HeadE=NULL;
for(CurrentB=HeadB;CurrentB!=NULL;CurrentB=CurrentB->next)//访问所有桶结点
{
for(CurrentE=CurrentB->p;CurrentE!=NULL;CurrentE=CurrentE->next)//访问桶中排序前的边结点
{
Edge *TEdge=new Edge;
TEdge->x=CurrentE->x;
TEdge->yMax=CurrentE->yMax;
TEdge->k=CurrentE->k;
TEdge->next=NULL;
AddAet(TEdge);//将该边插入临时Aet表
}
AetOrder();//使得Aet表按照x递增的顺序存放
T1=HeadE;//根据ymax抛弃扫描完的边结点
if(T1==NULL)
{
return;
}
while(CurrentB->ScanLine>=T1->yMax)//放弃该结点,Aet表指针后移
{
T1=T1->next;
HeadE=T1;
if(HeadE==NULL)
{
return;
}
}
if(T1->next!=NULL)
{
T2=T1;
T1=T2->next;
}
while(T1!=NULL)
{
if(CurrentB->ScanLine>=T1->yMax)//跳过一个结点
{
T2->next=T1->next;
T1->next=NULL;
T1=T2->next;
}
else
{
T2=T1;
T1=T2->next;
}
}
BOOL In=false;//设置一个BOOL变量In,初始值为假,相当于每次读2个点,以组成一个线段.
double xb,xe;//扫描线的起点和终点
for(T1=HeadE;T1!=NULL;T1=T1->next)//填充扫描线和多边形相交的区间
{
if(In==false)
{
xb=T1->x;
CurDeep=-(xb*A+CurrentB->ScanLine*B+D)/C;//z=-(Ax+By+D)/C
In=true;//每访问一个结点,把In值取反一次
}
else//如果In值为真,则填充从当前结点的x值开始到下一结点的x值结束的区间
{
xe=T1->x;
for(double x=xb;x<=xe;x++)
{
if(CurDeep>=ZB[ROUND(x)+200][CurrentB->ScanLine+200])//如果新的采样点的深度大于原采样点的深度,因为绘制每个面都会调用该函数,故以后的面中如果有更深度更大的点,则会覆盖以前的点的颜色.
{
ZB[ROUND(x)+200][CurrentB->ScanLine+200]=CurDeep;//xy坐标与数组下标保持一致,加200
mdc->SetPixel(ROUND(x),CurrentB->ScanLine,RGB[Face]);
}
CurDeep+=DeepStep;
}
In=false;
}
}
for(T1=HeadE;T1!=NULL;T1=T1->next)//边连贯性
{
T1->x=T1->x+T1->k;//x=x+1/k
}
}
delete HeadB;
delete CurrentB;
delete CurrentE;
delete HeadE;
}
//*****************有效边表算法开始***********************
void CTestView::CreatBucket()//初始化桶结点
{
int ScanMin,ScanMax;//确定扫描线的最小值和最大值
ScanMax=ScanMin=Point[0].y;
for(int i=1;i<Number;i++)
{
if(Point[i].y<ScanMin)
{
ScanMin=Point[i].y;//扫描线的最小值
}
if(Point[i].y>ScanMax)
{
ScanMax=Point[i].y;//扫描线的最大值
}
}
for(i=ScanMin;i<=ScanMax;i++)//建立桶结点
{
if(ScanMin==i)
{
HeadB=new Bucket;//建立桶的头结点
CurrentB=HeadB;//CurrentB为Bucket当前结点指针
CurrentB->ScanLine=ScanMin;
CurrentB->p=NULL;//没有连接边链表
CurrentB->next=NULL;
}
else//建立桶的其它结点
{
CurrentB->next=new Bucket;//新建一个桶结点
CurrentB=CurrentB->next;//使CurrentB指向新建的桶结点
CurrentB->ScanLine=i;
CurrentB->p=NULL;//没有连接边链表
CurrentB->next=NULL;
}
}
}
void CTestView::Et()//构造边表
{
for(int i=0;i<Number;i++)//访问每个顶点
{
CurrentB=HeadB;//从桶链表的头结点开始循环
int j=i+1;//边的第二个顶点,Point[i]和Point[j]构成边
if(j==Number) j=0;//保证多边形的闭合
if(Point[j].y>Point[i].y)//边在扫描线的上方
{
while(CurrentB->ScanLine!=Point[i].y)//在桶内寻找该边的yMin
{
CurrentB=CurrentB->next;//在桶内寻找该边的yMin
}
E[i].x=Point[i].x;//计算Aet表的值
E[i].yMax=Point[j].y;
E[i].k=double((Point[j].x-Point[i].x))/(Point[j].y-Point[i].y);//代表1/k
E[i].next=NULL;
CurrentE=CurrentB->p;//获得桶上链接边表的地址
if(CurrentE==NULL)//当前桶结点上没有链接边结点
{
CurrentE=&E[i];//赋边的起始地址
CurrentB->p=CurrentE;//第一个边结点直接连接到对应的桶中
}
else
{
while(CurrentE->next!=NULL)//如果当前边已连有边结点
{
CurrentE=CurrentE->next;//移动指针到当前边的最后一个边结点
}
CurrentE->next=&E[i];//把当前边接上去
}
}
if(Point[j].y<Point[i].y)//边在扫描线的下方
{
while(CurrentB->ScanLine!=Point[j].y)
{
CurrentB=CurrentB->next;
}
E[i].x=Point[j].x;
E[i].yMax=Point[i].y;
E[i].k=double((Point[i].x-Point[j].x))/(Point[i].y-Point[j].y);
E[i].next=NULL;
CurrentE=CurrentB->p;
if(CurrentE==NULL)
{
CurrentE=&E[i];
CurrentB->p=CurrentE;
}
else
{
while(CurrentE->next!=NULL)
{
CurrentE=CurrentE->next;
}
CurrentE->next=&E[i];
}
}
}
CurrentB=NULL;
CurrentE=NULL;
}
void CTestView::AddAet(Edge *NewEdge)//边插入Aet表
{
T1=HeadE;
if(T1==NULL)//Aet表为空,将Aet表置为TEdge
{
T1=NewEdge;
HeadE=T1;
}
else
{
while(T1->next!=NULL)//Aet表不为空,将TEdge连在该边之后
{
T1=T1->next;
}
T1->next=NewEdge;
}
}
void CTestView::AetOrder()//对Aet表进行排序
{
T1=HeadE;
if(T1==NULL)
{
return;
}
if(T1->next==NULL)//如果该Aet表没有再连Aet表
{
return;//桶结点只有一条边,不需要排序
}
else
{
if(T1->next->x<T1->x)//Aet表按x值排序
{
T2=T1->next;
T1->next=T2->next;
T2->next=T1;
HeadE=T2;
}
T2=HeadE;
T1=HeadE->next;
while(T1->next!=NULL)//继续两两比较相连的Aet表的x值,进行排序
{
if(T1->next->x<T1->x)
{
T2->next=T1->next;
T1->next=T1->next->next;
T2->next->next=T1;
T2=T2->next;
}
else
{
T2=T1;
T1=T1->next;
}
}
}
}
//*****************有效边表算法结束***********************