SVM-3-最优间隔分类器
参考http://www.cnblogs.com/jerrylead
在第一篇(SVM-1-问题描述)中我们得到了下面的优化问题:
把约束条件写成下面的形式:
这样就变成了在约束条件 gi(w)≤0 下,求 minδ,w,b 12||w||2 的最优化问题。
在KKT对偶互补条件中我们知道,当 αi>0 时, gi(w)=0 ,即 gi(w)=−yi(wTx∗+b)+1=0 ,也就是说 yi(wTx∗+b)=1 ,即函数间隔等于1。
而当 αi=0 时,一般而言 gi(w)<0 (当然,少数情况下,也许、大概、可能也会有 gi(w)=0 ,咱们忽略它,毕竟是少数。。。)。
我们看下面的图:
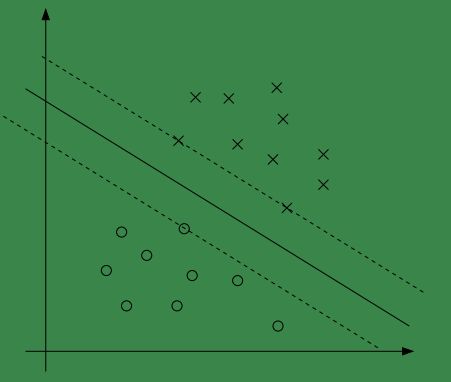
中间的实线是最大间隔超平面,上图中与超平面距离最近的样本有三个(这三个样本与超平面的距离相同),还记得在SVM-1-问题描述中我们将函数间距设为1吗?!也就是说,这三个样本与超平面的距离为1!
在图中还有两根虚线,它们与实线平行,且与实线的距离为1,也就是说,所有与超平面的距离为1的样本都在这两条虚线上。
之前说过距离为1,就要求 gi(w)=0,αi>0 ,从图中可以看出,满足距离为1的样本只是少数,大多数情况下距离都是大于1的,即大多数情况下 αi是等于0的 。
对于上面距离为1的样本有个专门的名字:“支持向量”。
现在将拉格朗日算子应用到我们的最优化问题中,构造拉格朗日函数如下:
注意到这里只有 αi 没有 βi 是因为原问题中没有等式约束,只有不等式约束。
下面考虑对偶问题
首先求解 minL(w,b,α) ,对于固定的 αi 该式的值只与 w和b 有关,我们可以令 θD(α)=minw,bL(w,b,α) ,为了求 θD(α) 的最小值,我们需要对 L 求 w和b 的偏导数:
将公式(2)带入(1)可得:
推到如下(公式太多直接截图。。。):
由公式(3)可知,最后一项为0,故上式可改写为:
上面是在 α 固定不变的前提下,求 minw,bL(w,b,α) ,现在开始求原问题的对偶问题:
注:
1、 <xi,xj> 表示向量的内积,与 (xi)Txj 等价。
2、 αi 此时当然已经不能再是一个固定的值了。
可以发现,上式是满足KKT条件的,因此我们可以用它来代替原始问题。
3、 现在只有一个参数 α 啦!
假如我们现在已经求出了 α :
我们首先可以通过公式 (2)w∗=∑miαiyixi ,计算得到 w∗ 。
然后可以通过下式计算得到 b∗ :
注:别问我为什么。。。。就是可以。。。
假设我们已经利用上面得到的参数训练完成一个模型,当输入一个新的样本时,将公式(2)带入 wTx+b 我们就可以进行预测:
即我们只需要计算输入样本与所有训练样本内积即可,另外还记得“支持向量”这个名词吧!对于上式中的 αi 只有很少一部分支持向量的 αi 才不等于0,因此并不需要与所有训练样本去做计算。