Aizu 1263 Network Mess 树的直径+构造
题目链接:点击打开链接
Network Mess
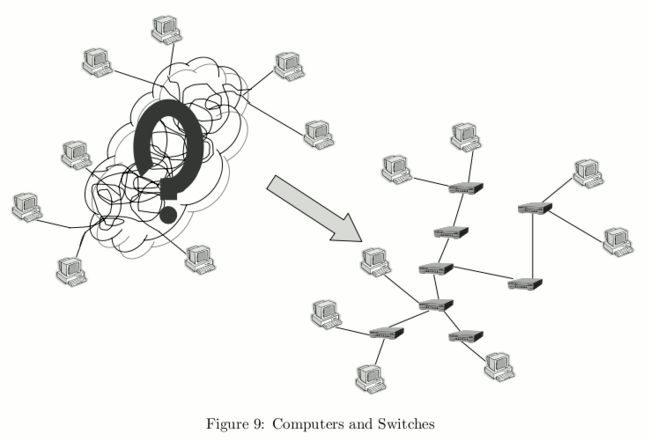
Gilbert is the network admin of Ginkgo company. His boss is mad about the messy network cables on the floor. He finally walked up to Gilbert and asked the lazy network admin to illustrate how computers and switches are connected. Since he is a programmer, he is very reluctant to move throughout the office and examine cables and switches with his eyes. He instead opted to get this job done by measurement and a little bit of mathematical thinking, sitting down in front of his computer all the time. Your job is to help him by writing a program to reconstruct the network topology from measurements.
There are a known number of computers and an unknown number of switches. Each computer is connected to one of the switches via a cable and to nothing else. Specifically, a computer is never connected to another computer directly, or never connected to two or more switches. Switches are connected via cables to form a tree (a connected undirected graph with no cycles). No switches are ‘useless.’ In other words, each switch is on the path between at least one pair of computers.
All in all, computers and switches together form a tree whose leaves are computers and whose internal nodes switches (See Figure 9).
Gilbert measures the distances between all pairs of computers. The distance between two com- puters is simply the number of switches on the path between the two, plus one. Or equivalently, it is the number of cables used to connect them. You may wonder how Gilbert can actually obtain these distances solely based on measurement. Well, he can do so by a very sophisticated statistical processing technique he invented. Please do not ask the details.
You are therefore given a matrix describing distances between leaves of a tree. Your job is to construct the tree from it.
Input
The input is a series of distance matrices, followed by a line consisting of a single '0'. Each distance matrix is formatted as follows.
N a11 a12 ... a1N a21 a22 ... a2N . . . . . . . . . . . . aN1 aN2 ... aNN
N is the size, i.e. the number of rows and the number of columns, of the matrix. aij gives the distance between the i-th leaf node (computer) and the j-th. You may assume 2 ≤ N ≤ 50 and the matrix is symmetric whose diagonal elements are all zeros. That is, aii = 0 and aij = aji for each i and j. Each non-diagonal element aij (i ≠j) satisfies 2 ≤ aij ≤ 30. You may assume there is always a solution. That is, there is a tree having the given distances between leaf nodes.
Output
For each distance matrix, find a tree having the given distances between leaf nodes. Then output the degree of each internal node (i.e. the number of cables adjoining each switch), all in a single line and in ascending order. Numbers in a line should be separated by a single space. A line should not contain any other characters, including trailing spaces.
Sample Input
4 0 2 2 2 2 0 2 2 2 2 0 2 2 2 2 0 4 0 2 4 4 2 0 4 4 4 4 0 2 4 4 2 0 2 0 12 12 0 0
Output for the Sample Input
4 2 3 3 2 2 2 2 2 2 2 2 2 2 2
http://www2.teu.ac.jp/icpc/
题意:
给出n表示有n台电脑,两两之间通过路由器连接(电脑是不能直接相连的)
再给出n*n的邻接矩阵表示任意两台电脑间的距离。
在局域网里加入树形的路由器使得满足给出的邻接矩阵。
输出每个路由器 连接的网线根数
思路:
首先电脑-路由器的距离恒为1,也就是说任意两台电脑间都>=2,所以去掉 (电脑-路由)这样的网线,所以给输入的矩阵-=2
这样我们就把电脑移动到了路由器上。
observe :
对于路由器构成的树,叶子节点上一定有电脑(当然电脑可能不只在叶子节点上)
所以一定存在2台电脑,使得这两台电脑在叶子节点上且这2个叶子节点间的路径是树的直径。所以找出这2台电脑
in a word, 找2个距离最远的节点。距离记为maxlen;
然后我们构造长度为maxlen的长链。
我们把第i台电脑加入这个树,则我们要找2个点满足:
1、这2个点已经加入了树
2、i点到这两个点形成的链的距离最短。
如此把n个节点加入树后再遍历一下树就能得到答案。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cmath>
#include <cstring>
#include <queue>
#include <set>
#include <map>
#include <vector>
template <class T>
inline bool rd(T &ret) {
char c; int sgn;
if (c = getchar(), c == EOF) return 0;
while (c != '-' && (c<'0' || c>'9')) c = getchar();
sgn = (c == '-') ? -1 : 1;
ret = (c == '-') ? 0 : (c - '0');
while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0');
ret *= sgn;
return 1;
}
template <class T>
inline void pt(T x) {
if (x <0) {
putchar('-');
x = -x;
}
if (x>9) pt(x / 10);
putchar(x % 10 + '0');
}
using namespace std;
const int inf = (int)1e8;
typedef pair<int, int> pii;
const int N = 1050;
struct Edge{
int from, to, nex;
}edge[1000000];
int head[N], edgenum, tot, dd[N]; //dd[i]表示树中的第i个点连了几台电脑,因为du[i]表示的是树边,所以i点的网线数=du[i]+dd[i]
void add(int u, int v){
Edge E = { u, v, head[u] };
edge[edgenum] = E;
head[u] = edgenum++;
}
void init(){
memset(head, -1, sizeof head); tot = 1; edgenum = 0;
}
void creat(int point, int len){
add(point, ++tot);
add(tot, point);
if (len) creat(tot, len - 1);
}
int D[N];
vector<int> bfs(int root, int len){ //寻找树上距离root距离为len的,返回这样的点的集合
// printf("Bfs:root=%d, dis=%d\n", root, len);
for (int i = 1; i <= tot; i++)D[i] = -1;
D[root] = 0;
queue<int>q; q.push(root);
vector<int>ans;
while (!q.empty()){
int u = q.front(); q.pop();
if (D[u] == len){
ans.push_back(u); continue;
}
for (int i = head[u]; ~i; i = edge[i].nex){
int v = edge[i].to;
if (D[v] == -1){
q.push(v); D[v] = D[u] + 1;
}
}
}
return ans;
}
int Jiao(vector<int>X, vector<int>Y){//找一个点ans使得ans同时存在X集合和Y集合(也就是找XY集合的交集)
for (int i = 0; i < X.size(); i++)
if (find(Y.begin(), Y.end(), X[i]) != Y.end())return X[i];
}
int n, dis[55][55], maxlen;
int vis[55];//vis[i]表示第i台电脑在树中的编号是几(vis[i]=0表示这个点尚未加入树
pii root;//root就是树的直径的两端
void input(){
init();
maxlen = -1;
memset(D, -1, sizeof D);
memset(dd, 0, sizeof dd);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++){
rd(dis[i][j]);
if (i == j)continue;
dis[i][j] -= 2;
if (dis[i][j]>maxlen){
maxlen = dis[i][j];
root = pii(i, j);
}
}
}
int du[N];
vector<int>ans;
void Find_ans(int u, int fa){
du[u] = 0;
for (int i = head[u]; ~i; i = edge[i].nex){
int v = edge[i].to; du[u]++;
if (v != fa)Find_ans(v, u);
}
ans.push_back(du[u] + dd[u]);
}
void put_tree(){
for (int i = 1; i <= tot; i++){
printf("%d:", i);
for (int j = head[i]; ~j; j = edge[j].nex)printf(" %d", edge[j].to);
puts("");
}
}
int main(){
while (~scanf("%d", &n), n){
input();
if (maxlen == 0){ printf("%d\n", n); continue; }
memset(vis, 0, sizeof vis);
vis[root.first] = tot;
creat(vis[root.first], maxlen - 1);
vis[root.second] = tot;
dd[vis[root.first]]++; dd[vis[root.second]]++;
// printf("最长链:(%d,%d), 长度:%d, 最长链在树中对应的点标:(%d,%d)\n", root.first, root.second, maxlen, vis[root.first], vis[root.second]);
for (int k = 1; k <= n; k++){
if (vis[k])continue;
int cha = inf;
pii hehe;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i != j && vis[i] && vis[j])
{
int C = dis[i][k] + dis[k][j] - dis[i][j];
if (cha > C) cha = C, hehe = pii(i, j);
}
int tmp = (dis[hehe.first][k] + dis[hehe.second][k] - dis[hehe.first][hehe.second]) / 2;
// printf("%d点找到的链是(%d,%d) %d,%d %d tmp=%d\n", k,hehe.first, hehe.second, dis[hehe.first][k], dis[hehe.second][k], dis[hehe.first][hehe.second], tmp);
int treepoint = Jiao(bfs(vis[hehe.first], dis[hehe.first][k] - tmp), bfs(vis[hehe.second], dis[hehe.second][k] - tmp));
// printf("%d点的支链长度为%d 分支点:%d\n",k, tmp, treepoint);
if (tmp == 0){
dd[treepoint] ++; vis[k] = treepoint; continue;
}
creat(treepoint, tmp - 1);
dd[tot]++;
vis[k] = tot;
// printf("%d在树中对应的点标:%d\n", k, vis[k]);
// put_tree(); puts("");
}
ans.clear();
Find_ans(root.first, -1);
sort(ans.begin(), ans.end());
for (int i = 0; i < ans.size(); i++)
printf("%d%c", ans[i], i + 1 == (int)ans.size() ? '\n' : ' ');
}
return 0;
}
/*
2
0 4
4 0
6
0 6 6 6 7 7
6 0 6 6 9 8
6 6 0 4 9 8
6 6 4 0 9 8
7 9 9 9 0 5
7 8 8 8 5 0
*/