一个点绕另一个点旋转a度 问题
公式如下,(x1,y1)为要转的点,(x2,y2)为中心点,如果是顺时针角度为-,
x=(x1-x2)cosθ-(y1-y2)sinθ+x2
y=(y1-y2)cosθ+(x1-x2)sinθ+y2
eg:bnu4226神技•八方鬼缚阵
就是简单的模拟加上点的旋转
在网络预赛中我们简单介绍了东方系列的格斗游戏,然而,东方系列(
Tohou Project
)最为经典的是它的纵卷轴弹幕射击游戏(
Lsy
和小陆同学却于此无爱~)。此类游戏中,弹幕被精心安排成特定几何形状,具有高度的视觉冲击力;音乐动感十足,与弹幕节奏配合得恰到好处;另外,符卡系统也是游戏的一大特色,只有玩家不放
Bomb
(雷,放出后有较大杀伤力并且此段时间内即使被弹幕击中也不会掉一条命)、不被弹幕击中且在规定时间内击破
Boss
才算成功破解此种符卡。以下是某些
BOSS
的弹幕:
好的,现在问题来了。有这么一种符卡,叫做八方鬼缚阵(呃,其实叫什么都无所谓),为了描述方便,我们现在以
Boss
的位置为原点建立一个直角坐标系,
boss
在第
1
秒的时候放出两颗子弹,位于(
0
,
0
),(
1
,
0
)。
第
2
秒时,除(
1
,
0
)点外所有子弹会复制自身,复制出来的子弹绕(
1
,
0
)点顺时针旋转
90
度到达新位置,新的弹幕组中最后一颗子弹位于(
1
,
1
)。
第
3
秒时,除(
1
,
1
)点外所有子弹复制自身,复制出来的子弹绕(
1
,
1
)再次顺时针旋转
90
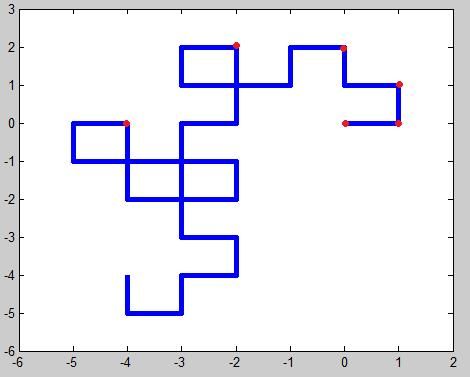
度。因此类推,下图给出了
5s
后的子弹分布:红点标出了每次旋转的中心,红色的(
0
,
0
)点表示原点。
下面请你输出
n
秒后所有子弹的位置以便
XsugarX
能成功地挑战这张符卡。
代码:
/*I believe xiaoxuzizhucan*/
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<iostream>
#include<math.h>
#include<algorithm>
using namespace std;
#define MOD 10000000
typedef struct
{
int x;
int y;
} node;
node q[1000005];
int main()
{
int cos=0;
int sin=-1;
//printf("%d\n",suan(0,0,1,0);
//
// int cos=0;
// int sin=1;
// int x=1;
// int y=1;
// int tx=0;
// int ty=0;
// int zx=tx*cos-ty*sin;
// int zy=tx*sin+ty*cos;
// printf("%d %d",zx,zy);
int test;
scanf("%d",&test);
while(test--)
{
int n;
scanf("%d",&n);
n--;
q[0].x=0;
q[0].y=0;
q[1].x=1;
q[1].y=0;
int count=2;
int xia=1;
while(n--)
{
int x2=q[xia].x;
int y2=q[xia].y;
int sbcount=count-1;
for(int i=sbcount-1; i>=0; i--)
{
int x1=q[i].x;
int y1=q[i].y;
if(x1==x2&&y1==y2)
continue;
if(i==0)
{
//q[count].x= x2+y1-y2;
q[count].x=(x1-x2)*cos-(y1-y2)*sin+x2;
// q[count].y=x2+y2-x1;
q[count].y= (y1-y2)*cos+(x1-x2)*sin+y2;
xia=count;
count++;
}
else
{
q[count].x=(x1-x2)*cos-(y1-y2)*sin+x2;
// q[count].y=x2+y2-x1;
q[count].y= (y1-y2)*cos+(x1-x2)*sin+y2;
count++;
}
}
}
for(int i=0; i<count; i++)
printf("%d %d\n",q[i].x,q[i].y);
}
}