动态规划入门(四)DP 基本思想与实现
POJ1160, post office。动态规划的经典题目。呃,又是经典题目,DP部分的经典题目怎就这么多。木有办法,事实就这样。
求:在村庄内建邮局,要使村庄到邮局的距离和最小。
设有m个村庄,分别为 V1 V2 V3 … Vm, 要建n个邮局,分别为P1 P2 P3 … Pn。
在DP的问题中,经常有从m个物体中选n个物体的情况,本题显然也属于这种情况。一般可以这样考虑:假设已经选了1个,那么就成了在m-1个中选n-1个的问题了。
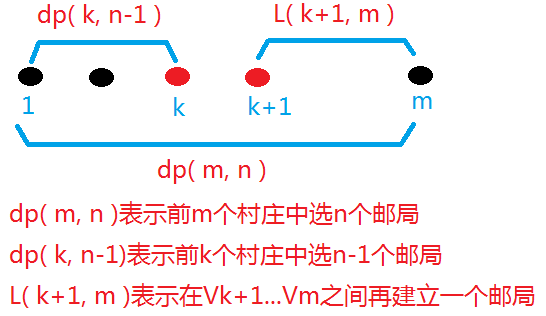
对于此题,也可以考虑先建一个邮局。建在哪里呢?不妨设,该邮局建在Vk+1..Vm之间的某个村庄里,而且规定Vk+1..Vm之间再不允许建立其他邮局了。因此,剩下的n-1个邮局必然出现在V1..Vk之间的村庄内,这样问题就转换成:在前k个村庄里选n-1个邮局的问题。
设dp( m,n )表示在V1…Vm之间建立n个邮局时的最短距离。
L( i, j )表示在Vi…Vj之间建立一个邮局的最短距离。
状态转换方程:
dp( m,n ) = Min( dp( k,n-1 ) + L( k+1,m ) ), 其中:1 <= k<m
编程实现:没啥说的,具体看代码。
心得;
DP的基本思想与分治法的基本思想是类似的;分析如下
1.都是组合子问题的解来求解求解原问题
2.分治法将问题划分为互不相交的子问题,递归地求解子问题,再将它们的解组合起来,求出原问题的解。
3.动态规划应用与子问题重叠的情况,即不同的子问题具有公共的子子问题。
4.动态规划的实现方法是自底向上法,将子问题按规模排序,按由从小到大的顺序进行求解,当求解某个子问题时,它所依赖的更小的子问题已经求解完毕,结果已保存,每个子问题只需求解一次。
编程实现注意事项:
//dp数组必须进行初始化 for(int i=1;i<=vNum;i++) dp[i][0]=INF;dp数组必须进行初始化,否则得不到正确结果
#include<iostream>
using namespace std;
//***************************常量定义***************************
const int V_MAX=300;
const int P_MAX=30;
const int INF=999999;
//**************************题目变量****************************
//全局变量全部初始化为0
int vNum;//村庄数
int pNum;//邮局数
int vPos[V_MAX];//村庄坐标
//*************************算法变量*****************************
int d[V_MAX][V_MAX];//d[i][j]表示第i个村庄与第j个村庄之间建一个邮局的最短距离
int dp[V_MAX][P_MAX];//dp[m][n]表示前m个村庄里面建n个邮局的最短距离
void solve()
{
//计算d[i][j]
for(int i=1;i<=vNum;i++)
for(int j=i+1;j<=vNum;j++)
d[i][j]=d[i][j-1]+(vPos[j]-vPos[(i+j)/2]);
//dp数组必须进行初始化
for(int i=1;i<=vNum;i++)
dp[i][0]=INF;
//计算dp[i][j]
for(int i=1;i<=vNum;i++)
for(int j=1;j<=i&&j<=pNum;j++)
{
int min=INF;
for(int k=j-1;k<i;k++)
{
if(dp[k][j-1]+d[k+1][i]<min)
min=dp[k][j-1]+d[k+1][i];
}
dp[i][j]=min;
}
cout<<dp[vNum][pNum];
}
int main()
{
cin>>vNum>>pNum;
for(int i=1;i<=vNum;i++)
cin>>vPos[i];
solve();
}
//dp数组必须进行初始化 for(int i=1;i<=vNum;i++) dp[i][0]=INF;
改进程序使之能输出选择的邮件序列,其思想与poj1458的思想类似,因为dp[m][n]的值取决于dp[k][n-1] (n-1=<k<=m),所以
int flag[V_MAX][P_MAX];//flag[m][n]存储计算dp[m][n]时所选择的dp[k][n-1]的k
代码如下:
<pre name="code" class="cpp">#include<iostream>
using namespace std;
//***************************常量定义***************************
const int V_MAX=300;
const int P_MAX=30;
const int INF=999999;
//**************************题目变量****************************
//全局变量全部初始化为0
int vNum;//村庄数
int pNum;//邮局数
int vPos[V_MAX];//村庄坐标
//*************************算法变量*****************************
int d[V_MAX][V_MAX];//d[i][j]表示第i个村庄与第j个村庄之间建一个邮局的最短距离
int dp[V_MAX][P_MAX];//dp[m][n]表示前m个村庄里面建n个邮局的最短距离
int flag[V_MAX][P_MAX];//flag[m][n]存储计算dp[m][n]时所选择的dp[k][n-1]的k
void solve()
{
//计算d[i][j]
for(int i=1;i<=vNum;i++)
for(int j=i+1;j<=vNum;j++)
d[i][j]=d[i][j-1]+(vPos[j]-vPos[(i+j)/2]);
//dp数组必须进行初始化
for(int i=1;i<=vNum;i++)
dp[i][0]=INF;
//计算dp[i][j]
for(int i=1;i<=vNum;i++)
for(int j=1;j<=i&&j<=pNum;j++)
{
int min=INF;
int chose=0;//存储选择最小值对应的k
for(int k=j-1;k<i;k++)
{
if(dp[k][j-1]+d[k+1][i]<min)
{
min=dp[k][j-1]+d[k+1][i];
chose=k;
}
}
dp[i][j]=min;
flag[i][j]=chose;
}
cout<<dp[vNum][pNum]<<endl;
}
void PrintPostOffice(int vNum,int pNum)
{
if((0==pNum)||pNum>vNum) return;
else
{
int k=flag[vNum][pNum];
PrintPostOffice(k,pNum-1);
cout<<vPos[(k+1+vNum)/2]<<" ";
}
}
int main()
{
cin>>vNum>>pNum;
for(int i=1;i<=vNum;i++)
cin>>vPos[i];
solve();
cout<<"选择的邮件序列"<<endl;
PrintPostOffice(vNum,pNum);
}