《机器学习实战》——无监督学习
基本原理:
无监督学习中,要划分的类别或者目标变量事先并不存在。摆在面前的是一堆无意义的数据集,要对其进行分组。其中最重要的算法有三个:K均值算法、基于Apriori的关联分析、基于FP-growth的关联分析。
1. K-means(K核算法)
随机确定k个初始点作为质心;
将数据集中每个点分配到一个蔟中,即为每个点找最近的簇心;
选择每个簇的簇心更新为该簇所有点的平均值。
优点:容易实现
缺点:可能收敛到局部最小值,无法达到全局最小值;大规模数据上收敛较慢。
提高聚簇性能的方法:
使用SSE(Sum of Squared Error 误差平方和)作为度量指标。
(1) 后处理:将具有最大SSE值的簇拆分,为保持簇总数不变,可以将某两个簇进行合并。
合并最近的质心:计算所有质心间的距离
合并两个使SSE增幅最小的质心:在所有可能的两个簇上重复处理直到找到最佳合并簇。
(2) 二分k-均值算法
将所有点合并为一个簇;
将该簇按照最小SSE原则一分为二;
选择其中一个簇继续划分,不断重复,直到达到用户指定的簇数为止。
2. 基于Apriori的关联分析
(1) 频繁项集:经常出现在一起的物品的集合。量化定义:满足最小支持度。
例如,一共N条记录,{豆奶,尿布}有3条,豆奶有8条
支持度:数据集中包含该项的记录所占的比例。豆奶支持度:8/N;{豆奶,尿布}支持度:3/N
置信度:针对诸如{豆奶}——>{尿布}的关联规则定义的。这条关联规则置信度为:支持度{豆奶,尿布} / 支持度{尿布}
Apriori原理:如果某个项集是频繁的,那么它的所有子集也是频繁的;如果某个子集是非频繁的,那么它的所有超集也是非频繁的。
使用Apriori原理可以避免项集数目的指数增长,从而在合理的时间内计算出频繁项集。
图1 所有可能的项集,非频繁项集用灰色表示。
Apriori的两个输入参数:最小支持度、数据集。算法步骤为:
生成单个物品的项集列表;
扫描交易记录查看哪些项集满足最小支持度的要求,不满足最小支持度的集合将被去掉;
剩下的集合进行组合以生成包含两个元素的项集;
重新扫描,去掉不满足最小支持度的项集;
直到所有最小项集被去掉。
(2) 关联规则:两个物品之间可能存在的很强的关系。量化定义:满足最小可信度/
包括两项:发现频繁项集、发现关联规则。
减少需测试的规则数目:如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求。
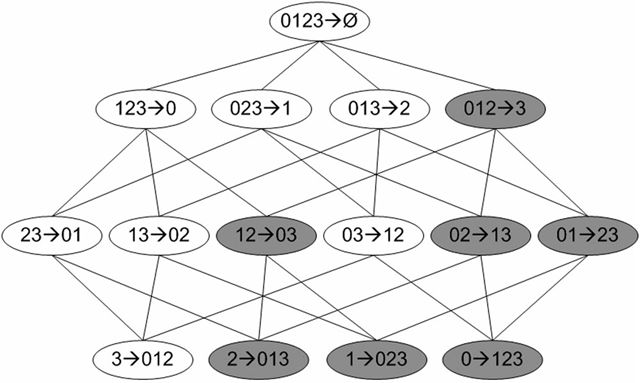
图2 频繁项集{0,1,2,3}的关联规则网格示意图.阴影区给出的是低可信度规则。
3. 基于FP-growth的关联分析
FP-growth是基于Apriori,但是采用了不同的技术——FP树,可以更高效地发现频繁项集(只需两次扫描:一次建树,一次挖掘频繁项集)。
FP树会存储项集的出现频率,而每个项集会以路径的方式存储在树中。
存在相似元素的集合会共享树的一部分。只有当集合间完全不同时,树才会分叉。
相似项之间的链接,即节点链接,用于发现相似项的位置。
工作流程:
构建FP树:
第一遍扫描数据集,记录每一项出现频率。如果某元素出现不频繁,那么超集也是不频繁的,可以直接去掉。第二遍只考虑频繁项集。
从FP树中获得条件模式基(以所查找的元素项为结尾的路径集合)
利用条件模式基,构建得到一个条件FP树
重复直到树包含一个元素