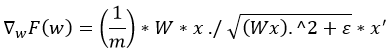[机器学习] UFLDL笔记 - ICA（Independent Component Analysis）（Representation）

引言

　机器学习栏目记录我在学习Machine Learning过程的一些心得笔记，涵盖线性回归、逻辑回归、Softmax回归、神经网络和SVM等等，主要学习资料来自Standford Ag老师的教程，同时也查阅并参考了大量网上的相关资料（在后面列出）。

　本文主要记录我在学习ICA（独立成分分析）过程中的心得笔记，对于ICA模型的理解和疑问，也纠正网络上一些Tutorial、资料和博文中的错误，欢迎大家一起讨论。
　全文共分为两个部分：
　ICA: Representation：ICA的模型描述； 　
　ICA: Code：ICA的代码实现。

前言　

　本文主要介绍ICA的基础知识，源自于我在学习ICA过程中的笔记资料，包括了我个人对ICA模型的理解以及网络资料，引用部分我都会标注出来文章小节安排如下：
　1）ICA的背景
　2）ICA的概述
　3）目标函数
　4）优化参数
　5）优化参数 - 实践
　7）参考资料
　8）结语

ICA的背景　

　独立成分分析（Independent Component Analysis, ICA）是近年来出现的一种强有力的数据分析工具（Hyvarinen A, Karhunen J, Oja E, 2001; Roberts S J, Everson R, 2001）。1994年由Comon给出了ICA的一个较为严格的数学定义，其思想最早是由Heranlt和Jutten于1986年提出来的。
　ICA从出现到现在虽然时间不长，然而无论从理论上还是应用上，它正受到越来越多的关注，成为国内外研究的一个热点。特别是从应用角度看，它的应用领域与应用前景都是非常广阔的，目前主要应用于盲源分离、图像处理、语言识别、通信、生物医学信号处理、脑功能成像研究、故障诊断、特征提取、金融时间序列分析和数据挖掘等。
　ICA是一种用来从多变量（多维）统计数据里找到隐含的因素或成分的方法，被认为是主成分分析（Principal Component Analysis, PCA）和因子分析（Factor Analysis）的一种扩展。对于盲源分离问题，ICA是指在只知道混合信号，而不知道源信号、噪声以及混合机制的情况下，分离或近似地分离出源信号的一种分析过程。
引自：独立成分分析（ICA）

ICA的概述　

　稀疏编码算法可以为样本数据学习到一个超完备基（over-complete basis），也就是基底（basis）中基向量（basis vector）的个数大于数据的维、数，那么这些基向量之间一定是线性相关的。超完备基的好处是能更有效地找出隐含在输入数据内部的结构与模式，问题是对于超完备基来说，系数 a_i 不再由输入向量 x 唯一确定。
　ICA（Independent Component Analysis）可以为样本数据学习得到一组线性独立（linearly independent）的基向量，也就是基底中基向量的个数小于等于数据的维数，同时这还是一个标准正交基（orthonormal basis）。
　与稀疏编码类似，给定数据 x，ICA希望学习得到一组基向量 —— 以列向量形式构成的矩阵 W，满足：
　1）特征是稀疏的（sparse）；
　2）基底是正交的（orthonormal）。
　与稀疏编码不同的是，在稀疏编码中，矩阵 A 用于将特征 s 映射到原始数据，而在ICA中，矩阵 W 工作的方向相反，是将原始数据 x 映射到特征。
　补充：标准正交基
　在线性代数中，一个内积空间的正交基（orthogonal basis）是元素两两正交的基。称基中的元素为基向量。假若，一个正交基的基向量的模长都是单位长度1，则称这正交基为标准正交基（Orthonormal basis）。
　具体来说，
　如果一组基向量 (Φ₁, Φ₂, …, Φ_n) 满足 Φ_i · Φ_j = 0 ( i≠j )，Φ_i · Φ_j = 1 ( i=j )，那么称为标准正交基。
　

目标函数（Objective function）　

　ICA模型的目标函数如下：
　
　

　直观地看，这是样本数据 x 经过参数矩阵 W 线性变换后的结果的L1范数，实际上也就是描述样本数据的特征。将ICA的目标函数与Sparse coding的目标函数对比：
　
　
　
　可以发现，
　ICA目标函数等价于在稀疏编码中特征 s 的稀疏惩罚项（sparsity penalty），这其实就是稀疏性约束，保证了ICA得到的特征是稀疏的。加入标准正交性约束（orthonormality constraint）后，独立成分分析相当于求解如下优化问题：
　
　

　这便是标准正交ICA的目标函数。与深度学习中的通常情况一样，这个问题没有简单的解析解（simple analytic solution），因此需要使用梯度下降来求解，而由于标准正交性约束（orthonormality constraint），又需要每次梯度下降迭代之后，将新的基映射回正交基空间中（以此保证正交性约束）。
　
　通过观察可知，约束 WW^T = I 隐含着另外两个约束：
　第一，因为要学习到一组标准正交基，所以基向量的个数必须小于输入数据的维度；
　第二，数据必须经过无正则 ZCA白化（也即，ε 设为0）。

疑问：？？？
　这里 WW^T = I 隐含的第二点约束“数据必须经过无正则 ZCA白化”还没有理解。

补充：白化
　白化是一种重要的预处理过程，其目的就是降低输入数据的冗余性，使得经过白化处理的输入数据具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。
　白化处理分PCA白化和ZCA白化，PCA白化保证数据各维度的方差为1，而ZCA白化保证数据各维度的方差相同。PCA白化可以用于降维也可以去相关性，而ZCA白化主要用于去相关性，且尽量使白化后的数据接近原始输入数据。
　

优化参数（Optimizing）　

　针对ICA的目标函数和约束条件，可以使用梯度下降法，并在梯度下降的每一步中增加投影（projection ）步骤，以满足标准正交约束。过程如下：
　
　
　
　在实际中，
　学习速率 α 是可变的，使用一个线搜索算法（line-search algorithm）来加速梯度下降；
　投影步骤通过设置 W<—(WW^T)^-1/2W 来完成，这实际上可以看成就是ZCA白化。
　
疑问：？？？　
　为何参数矩阵的正交化可以看作是ZCA白化，还没有理解。

补充：线性搜索算法
　例如有数组data，含1000个元素，要从里面找 x。线性搜索算法，就是从头找到尾，依次判断 data[0] 是否等于 x，如果不是则判断 data[1]，data[2]，..，依次类推，一直找到最后一个data[999]。线性搜索算法速度最慢，但是适用性最广。
　

优化参数（Optimizing） - 实践　

　ICA的具体优化过程在UFLDL Tutorial中并没有进行详细的讲解，造成了很多人的误解，并且没有办法实现课后练习（主要是代价函数及梯度求解错误导致线性搜索陷入死循环）。这里给出正确的分析和求解过程。
　首先回顾标准正交ICA的目标函数：
　
　

　通过分析ICA模型的目标函数可以发现该函数是一个L1范数，在 0 点处不可微，也就影响了梯度方法的应用。尽管可以通过其他非梯度下降方法避开这一问题，但是这里通过使用近似值“平滑” L1 范数的方法解决此难题。
　即使用 ( x2+ε )^1/2 代替 |x|，对 L1 范数进行平滑，其中 ε 是“平滑参数”（”smoothing parameter”）。
　因此，
　ICA模型重写为：
　
　 其中，
　

　为了表述便利，并考虑均值化问题，最终ICA的目标函数及对W的梯度如下，
　标准正交ICA的目标函数：
　

　标准正交ICA的目标函数对W的梯度：
　

关于正交化步骤
　注意一点，正交化通过 W<—(WW^T)^-1/2W 来完成，其实现为：
　
　而不是
　

　因此，ICA的梯度下降算法如下：
　1. 随机初始化 W；
　2. 重复以下步骤直至收敛：
　　2.1 计算梯度 ▽_wF(W)，并更新参数：
　　
　　2.2 正交化：
　　
　其中省去了线性搜索步骤，具体可参考代码实现。
　
　
备注：
　UFLDL Tutorial中并没有详细详解ICA的优化过程，导致很多同学在学习过程中遇到问题并产生错误理解。这里给出我在网上看到的资料中存在的理解错误和一些不容易理解的地方，供参考。
　1）UFLDL - Deriving gradients using the backpropagation idea
　地址：
　http://ufldl.stanford.edu/wiki/index.php/Deriving_gradients_using_the_backpropagation_idea
　文中示例3：ICA reconstruction cost，所提到的 reconstruction cost term 如下：
　
　
　
　这并不是ICA的代价函数，而是RICA（Reconstruction ICA）的一个soft reconstruction penalty，因此示例3其实是在对这个重建代价项求导。

　1）2）Deep learning：三十三(ICA模型) 和 Deep learning：三十九(ICA模型练习)
　地址（三十三(ICA模型) ）：
　http://www.cnblogs.com/tornadomeet/archive/2013/04/25/3041963.html
　地址（三十九(ICA模型练习)）：
　http://www.cnblogs.com/tornadomeet/archive/2013/05/07/3065953.html
　tornadomeet同学在ICA这两篇博文中对ICA的目标函数理解有误，我猜测也是和UFLDL中不清楚的讲解有关，这里指出一下，即ICA的目标函数是：
　
　
　
　而
　
　

　是RICA的soft reconstruction penalty，对应的RICA的目标函数是：
　
　

　具体可以参考UFLDL Tutorial新版中对RICA的讲解：
　http://ufldl.stanford.edu/tutorial/unsupervised/RICA/
　简单来说，
　ICA模型的正交性限制带来了一些缺点，换句话说，特征矩阵W的特征数量（即基向量数量）大于原始数据维度会产生优化方面的困难，并导致训练时间过长。RICA是在ICA基础上的扩展，通过将正交性约束改为一个soft reconstruction penalty，克服了ICA模型的缺陷。
　另外，我在学习UFLDL过程中经常会查阅到tornadomeet同学的博文，这里表示感激。
　
　

讨论（Discussion）　

1）ICA与PCA
　1）
　可以感性上对比下ICA和PCA的区别，
　一方面，PCA是将原始数据降维并提取出不相关的属性，而ICA是将原始数据降维并提取出相互独立的属性。
　另一方面，PCA目的是找到这样一组分量表示，使得重构误差最小，即最能代表原事物的特征。ICA的目的是找到这样一组分量表示，使得每个分量最大化独立，能够发现一些隐藏因素。由此可见，ICA的条件比PCA更强些。
　参考：一些知识点的初步理解_9(独立成分分析-ICA,ing…)
　2）
　ICA与PCA的区别在于：
　ICA要求找到最大独立的方向，各个成分是独立的；PCA要求找到最大方差的方向，各个成分是正交的。
　参考：独立成分分析（ICA）
　3）
　总的来说，ICA认为观测信号是若干个统计独立的分量的线性组合，ICA要做的是一个解混过程。而PCA是一个信息提取的过程，将原始数据降维，现已成为ICA将数据标准化的预处理步骤。
　参考：独立成分分析 ( ICA ) 与主成分分析 ( PCA ) 的区别在哪里？
　

参考资料　

　UFLDL Tutorial (new version)
　http://ufldl.stanford.edu/tutorial/
　UFLDL Tutorial (old version)
　http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial
　Deep learning：三十三(ICA模型)
　http://www.cnblogs.com/tornadomeet/archive/2013/04/25/3041963.html
　一些知识点的初步理解_9(独立成分分析-ICA,ing…)
　http://www.cnblogs.com/tornadomeet/archive/2012/12/30/2839841.html
　独立成分分析（Independent Component Analysis）
　http://www.cnblogs.com/jerrylead/archive/2011/04/19/2021071.html
　独立成分分析（ICA）
　http://blog.sciencenet.cn/blog-479412-391808.html
　机器学习中的范数规则化之（一）L0、L1与L2范数
　http://blog.csdn.net/zouxy09/article/details/24971995
　

结语　

　下一篇文章会撰写ICA模型的训练过程、代码以及实验结果（对应UFLDL的课后练习），谢谢！

　本文的文字、公式和图形都是笔者根据所学所看的资料经过思考后认真整理和撰写编制的，如有朋友转载，希望可以注明出处：　
　[机器学习] UFLDL笔记 - ICA（Independent Component Analysis）（Representation）
　http://blog.csdn.net/walilk/article/details/50468140